Тангенс и котангенс. онлайн калькулятор

Тангенс — это отношение…

Итак, есть два определения:

1. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

   Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

2. Тангенс – это отношение синуса к косинусу.

   Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Примеры построения графиков функций

      Пример 1. Построить

y = x3 + 8×2 + 16x + 128

(1)

      Решение. функции (1) является вся числовая прямая.

      Функция (1) не является ни ни .

      Функция (1) не является .

      у графика функции (1) нет, так как для любого числа   x

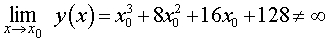
     Проверим, есть ли у графика функции (1) . Поскольку

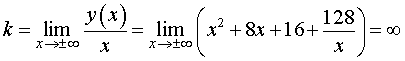
то .

      Теперь вычислим производную функции (1):

y’ (x) = 3×2 + 16x + 16 .

      Поскольку   y’ (x)   существует для всех , то все функции являются ее , то есть точками, в которых

y’ (x) = 0 .

      Найдем стационарные точки функции (1), интервалы, на которых   y’ (x)   сохраняет знак, а также . Для этого

3×2 + 16x + 16 = 0.

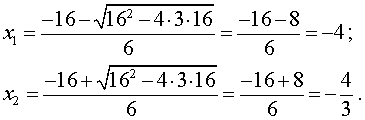
      Изобразим на рисунке 1 диаграмму знаков производной   y’ (x)

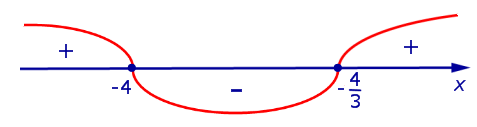
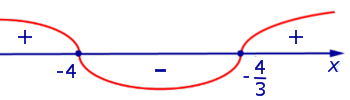
Рис.1

      На интервалах и производная   y’ (x)   положительна, , функция (1) . На интервале производная   y’ (x)   отрицательна, , функция (1) . Схематически поведение функции (1) изображено на рисунке 2.

Рис.2

      При переходе через точку   x = – 4   производная функции   y’ (x)   меняет знак с   «+»   на   «–» . точка   x = – 4   является функции (1). При переходе через точку производная функции   y’ (x)   меняет знак с   «–»   на   «+» . точка является функции (1).

      Найдем (1) в стационарных точках:

y (–4) = 256 ,

     Теперь вычислим функции (1):

y» (x) = (y’ (x))’ = (3×2 + 16x + 16)’ = 6x + 16 .

y» (x) = (y’ (x))’ == (3×2 + 16x + 16)’ == 6x + 16 .

     Вторая производная   y» (x)   обращается в нуль при . Изобразим на рисунке 3 диаграмму знаков второй производной   y» (x)

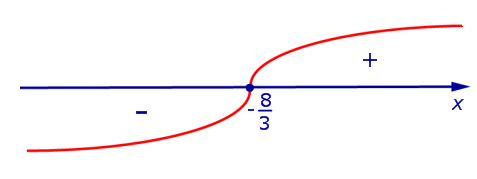
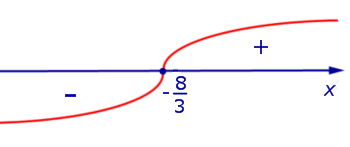
Рис.3

      При переходе через точку вторая производная функции   y» (x)   меняет знак с   «–»   на   «+» . Следовательно, – графика функции (1). При функция (1) , при функция (1) .

      Дополним схему поведения функции, представленную на рисунке 2, новыми данными о направлении выпуклости функции (рис. 4).

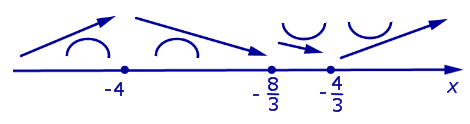
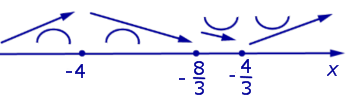
Рис.4

      Для того, чтобы найти точки пересечения функции (1) с осью   Ox ,   решим уравнение

x3 + 8×2 + 16x + 128 = 0 ,

x2 (x + 8) + 16 (x + 8) = 0 ,

(x + 8) (x2 + 16) = 0 .

      Таким образом, точка   (– 8; 0)   является единственной точкой пересечения графика функции (1) с осью   Ox .   Точкой пересечения графика функции (1) с осью   Oy   будет точка   (0; 128) .

      На схеме поведения функции, представленной на рисунке 4, добавим информацию о знаках функции (1) (рис. 5).

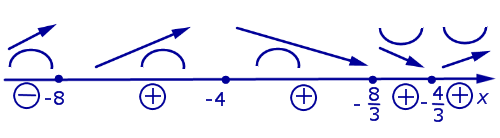
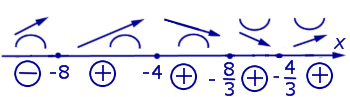
Рис.5

     Принимая во внимание результаты исследования поведения функции (1) (большая часть данных компактно представлена на рисунке 5), мы можем построить график функции (1) (рис.6):

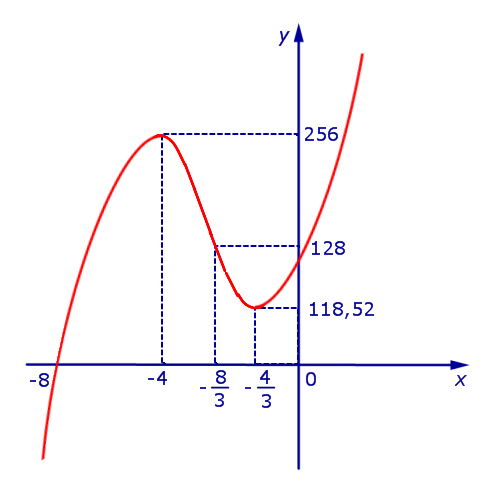
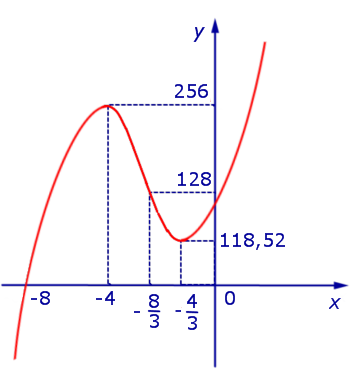
Рис.6

      Пример 2. Построить

(2)

      Решение. функции (2) является вся числовая прямая, за исключением точки   x = 0 ,   то есть .

      Функция (2) не является ни ни .

      Функция (2) не является .

      Прямая   x = 0   является графика функции (2), так как

      Для того, чтобы выяснить, имеются ли у графика функции (2) , представим правую часть формулы (2) в другом виде:

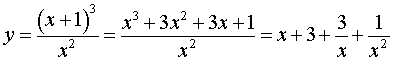(3)

      Из формулы (3) получаем равенство

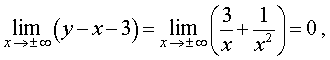
откуда вытекает, что прямая

y = x + 3

является наклонной асимптотой графика функции (2), как при , так и при .

      Теперь вычислим производную функции (2). Проще всего это сделать, воспользовавшись формулой (3):

(4)

      Для того, чтобы найти функции (2), преобразуем правую часть формулы (4):

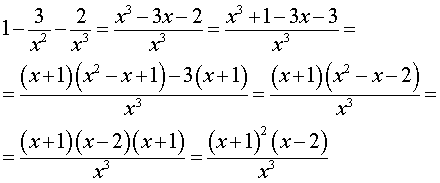
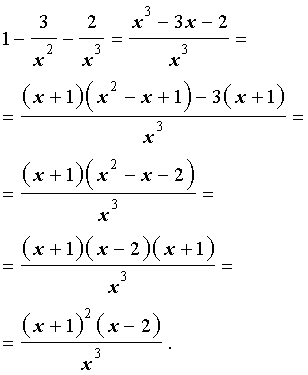
      Следовательно,

(5)

и стационарными точками функции (2) являются точки   x = – 1   и   x = 2 .   Поскольку   y’ (x)   не существует при   x = 0 ,   то функции (2) являются точки

x = – 1 ,   x = 0,   x = 2 .

      Изобразим на рисунке 7 диаграмму знаков производной   y’ (x)

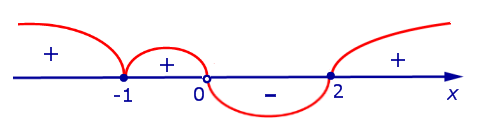
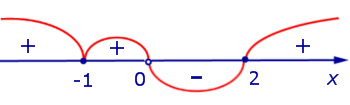
Рис.7

      На интервалах , и производная   y’ (x)   положительна, , функция (2) на этих интервалах. На интервале   (0, 2)   производная   y’ (x)   отрицательна, , функция (2) на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.

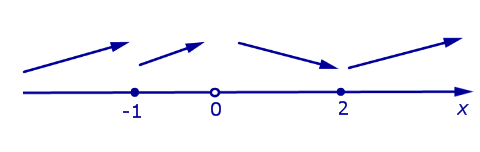
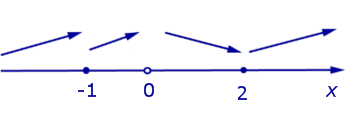
Рис.8

      При переходе через точку   x = – 1   производная функции   y’ (x)   знак не меняет, значит, в этой точке экстремума нет. При переходе через точку   x = 2   производная функции   y’ (x)   меняет знак с   «–»   на   «+» .   точка   x = 2   является функции (2).

      Найдем (1) в стационарных точках:

y (–1) = 0 ,

     Теперь перейдем к вычислению функции (2). Проще всего это сделать, воспользовавшись формулой (4):

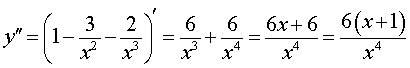
      Вторая производная   y» (x)   обращается в нуль при   x = – 1 .   Изобразим на рисунке 9 диаграмму знаков второй производной   y» (x)

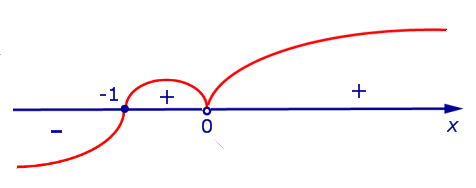
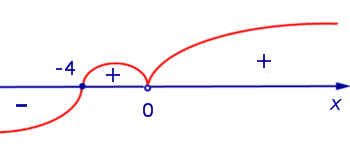
Рис.9

      При переходе через точку   x = – 1   вторая производная функции   y» (x)   меняет знак с   «–»   на   «+» . Следовательно,   x = – 1   – графика функции (2). При   x < – 1   функция (2) , при   x > – 1   функция (2) .

      Дополним схему поведения функции, представленную на рисунке 8, данными о направлении выпуклости функции (рис. 10).

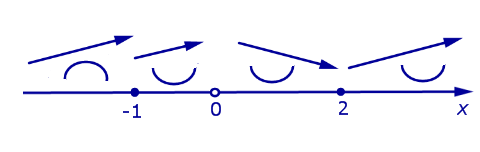
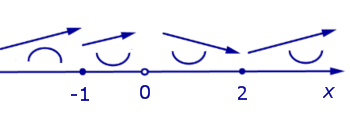
Рис.10

      Найдем точки пересечения функции (2) с осями координат: точка   (– 1; 0)   является единственной точкой пересечения графика функции (2) с осью   Ox ,   а точек пересечения графика функции (2) с осью   Oy   нет, поскольку  

      На схеме поведения функции, представленной на рисунке 10, добавим информацию о знаках функции (2) (рис. 11).

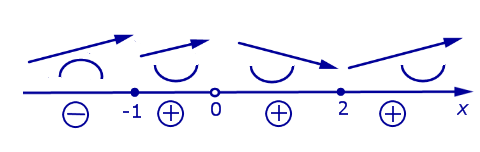
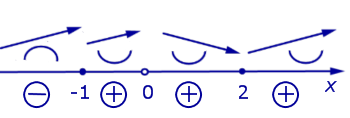
Рис.11

     Принимая во внимание результаты исследования поведения функции (2) (большая часть данных компактно представлена на схеме рисунка 11), мы можем построить график функции (2) (рис.12):

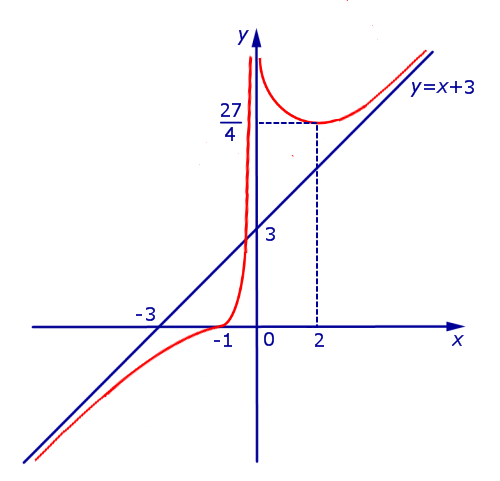
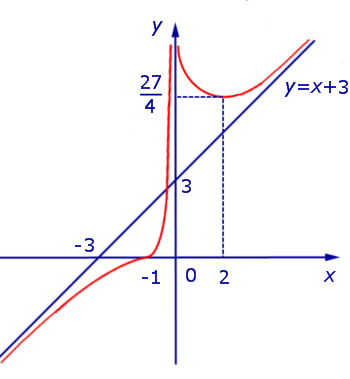
Рис.12

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса определенными уравнениями. Вкратце это будет выглядеть так:

Эта красота означает следующее:

Наша текущая позиция — y

Наше ускорение (2-я производная, или у”) — обратно нашей текущей позиции (-y)

Это справедливо и для синуса, и для косинуса. Сначала я просто ненавидел это определение; оно такое непохожее на нашу визуализацию. Я не понимал, что оно описывало суть синуса: «ускорение, обратное текущей позиции».

И вспомните как синус и е связаны? Ну, e^x можно описать уравнением:

То же уравнение с положительным знаком («ускорение равно текущей позиции»)! Когда синус — это «высота окружности», очень тяжело проследить связь с е.

Одним из моих серьезнейших математических сожалений является то, что я еще не изучил дифференциальные уравнения. Но я хочу это сделать, и подозреваю, что правильное понимание синуса и экспоненты сыграют в этом решающую роль.

Использование функций в Excel 2007

Вы уже можете делать вычисления в Excel 2007, и уже использовали математическую функцию TAN, которая вычисляет тангенс. Кроме того, при выполнении сложения чисел Вы использовали функцию СУММ, которая вычисляет сумму ряда чисел.

В программе Excel встроено огромное количество других самых разнообразных функций. Функции в Excel используются и для вычислений, и для выполнения логических операций, и для операций с датами и текстом. По каждой функции в Excel есть справка, и Вы вполне можете самостоятельно узнать, как использовать ту или иную новую для Вас функцию.

Рассмотрим на практике использование некоторых функций Excel. Когда Вы выделяете ячейку, и затем нажимаете на fx перед строкой формул, по умолчанию Вам предложат функции Excel из категории 10 недавно использовавшихся функций. Но Вы можете в списке выбрать также следующие виды функций:

• полный алфавитный перечень
• финансовые
• дата и время
• математические
• статистические

и многие другие категории.

Давайте сначала рассмотрим математические функции Excel, как наиболее употребительные.

• ABS: возвращает модуль (положительное значение) числа. Поставьте в ячейку число -3, затем выделите другую ячейку, нажмите fx, выберите в категории математические функцию ABS, и вместо указания числа нажмите на ячейку с числом -3. В ячейке с функцией ABS появится значение 3.
• COS, SIN, TAN: возвращает значение косинуса, синуса, тангенса заданного числа, или значения заданной ячейки. Котангенса в функциях Excel нет, наверно, потому, что котангенс в формуле легко заменить единицей, деленной на тангенс.
• EXP: возвращает экспоненту заданного числа. Не знаете, что такое экспонента? Нажимаете на ссылку ниже: Справка по этой функции. Оказывается, экспонента — это число e (2,718…), возведенное в указанную степень. То есть экспонента числа -3 — это e в степени -3. Выделяете ячейку, выбираете EXP, и когда появится окошко с выбором числа, вместо числа указываете ячейку с числом.
• LN, LOG: возвращает значения натурального и десятичного логарифмов числа. Логарифмы вычисляются для положительных чисел, для числа -3 эти функции выдадут ошибку. Можно вычислить логарифм абсолютного значения (модуля) числа -3. Для этого выбираете функцию логарифма, и прямо в окошке для числа пишете ABS, ставите открывающую скобку, затем нажимаете на ячейку с числом -3, затем ставите закрывающую скобку. Нажимаете ОК. В ячейке появится значение логарифма, а в строке формул Excel — формула, например:=LN(ABS(B1)), где B1 — адрес ячейки с числом.
• LOG: требует уже два значения: само число и основание логарифма. Выберите эту функцию, и в окошки поставьте либо числа напрямую, либо ставите в окошки курсор, и выбираете ячейку с соответствующим числом. Адреса ячеек можно прописывать также и с клавиатуры, только следите, чтобы была английская раскладка клавиатуры.
• СУММ: можно суммировать отдельные числа, а можно целые диапазоны чисел: во втором случае достаточно при указании числа выделить соответствующий диапазон ячеек.

Функции в Excel могут быть не только математические. Хотите, например, узнать, сколько дней Вы прожили? Напишите в ячейку дату своего рождения в формате ДД.ММ.ГГГГ, например, 31.03.1971 (это мой день рождения). В другую ячейку вставьте функцию СЕГОДНЯ (она находится в категории Дата и время). В третью ячейку введите =, затем укажите ячейку с сегодняшней датой, затем поставьте — (минус), затем укажите ячейку с датой рождения. Получится что-то вроде:

=D2-D1, где D2 и D1 — адреса соответствующих ячеек.

И все, больше ничего не нужно делать. В ячейке будет количество дней между указанными датами, в данном случае, количество дней, которые Вы прожили.

Напоследок рассмотрим одну из логических функций ЕСЛИ. Простейший пример: введите в две ячейки какие-нибудь числа.

В третьей ячейке выберите функцию ЕСЛИ, в окошке Лог_выражение: выберите одну ячейку с числом, затем напишите =, выберите вторую ячейку.

В окошке Значение_если_истина: напишите слово равны, а в окошке Значение_если_ложь: напишите не равны. Нажмите ОК.

Если значения в ячейках не будут совпадать, функция ЕСЛИ выдаст «не равны», если будут, функция выдаст «равны».

Более подробные сведения Вы можете получить в разделах «Все курсы» и «Полезности», в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.

Также Вы можете подписаться на блог, и узнавать о всех новых статьях. Это не займет много времени. Просто нажмите на ссылку ниже:

    Подписаться на блог: Дорога к Бизнесу за Компьютером

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

В частности,

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Как в Excel построить синусоиду

• Как построить график синусоиды в Excel.
• Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:
• =SIN(4*C4)
• Требуется построить график функции.
• Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.
• В итоги у нас должна получится таблица вида:

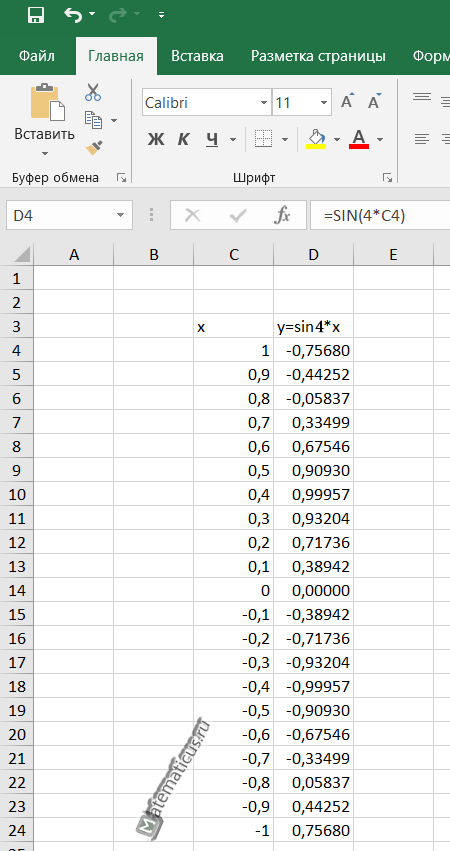
x	y=sin4*x
1	-0,75680
0,9	-0,44252
0,8	-0,05837
0,7	0,33499
0,6	0,67546
0,5	0,90930
0,4	0,99957
0,3	0,93204
0,2	0,71736
0,1	0,38942
	0,00000
-0,1	-0,38942
-0,2	-0,71736
-0,3	-0,93204
-0,4	-0,99957
-0,5	-0,90930
-0,6	-0,67546
-0,7	-0,33499
-0,8	0,05837
-0,9	0,44252
-1	0,75680

Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

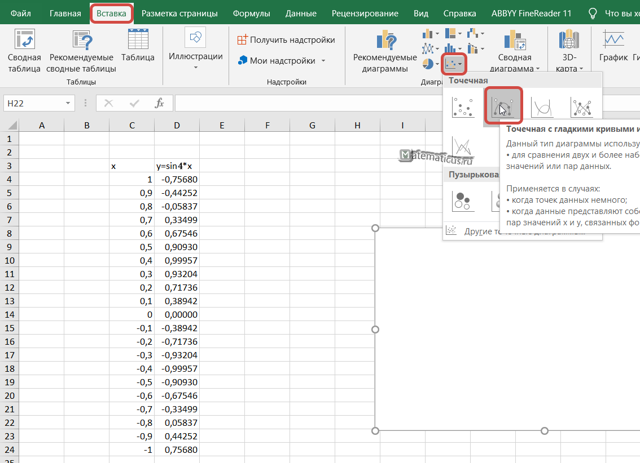
Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

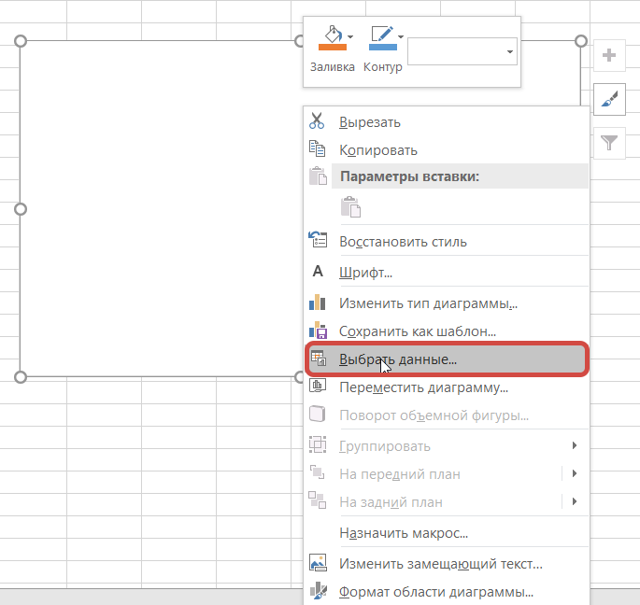
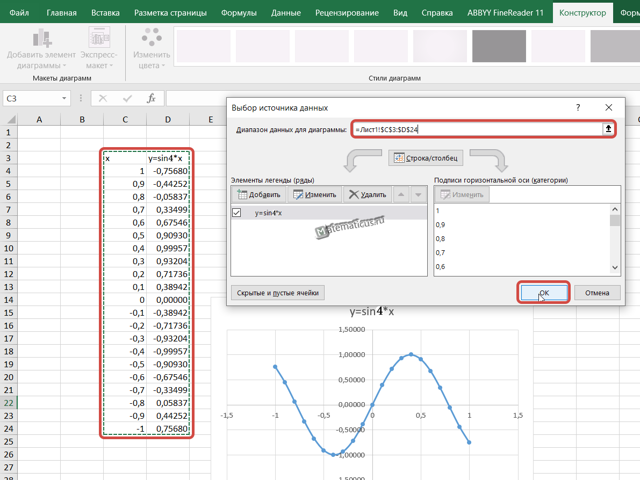
В итоги у нас получается график вида.

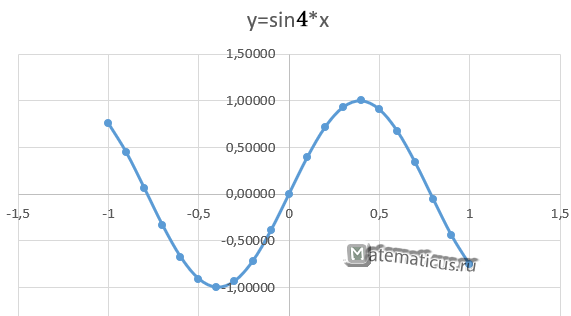
Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

Построение графика функций SINH и COSH в Excel

Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Исходные данные:

Формула для нахождения синусов гиперболических:

=SINH(A2:A12)

Формула для нахождения косинусов гиперболических:

=COSH(A2:A12)

Таблица полученных значений:

Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Пошаговая инструкция построения графика функции в Excel 2007

1. Запускаем программу, которая создаст новый чистый лист книги Excel. Подписываем два столбца (B и С), в одном из которых будет записан аргумент x, а в другом — функция y.
2. Заносим в столбец B, значения аргументов x, начиная с ячейки B3. Можно воспользоваться автоматическим копированием ячеек, предварительно задав шаг (разница между ближайшими значениями аргумента). Значения аргумента x можно задать произвольно, но чаще вводят значения близкие к нулю с учетом отрицательных и положительных значений. Очень хорошо будет смотреться график, если значения будут браться симметрично относительно нуля. Предлагаем выбрать значения в промежутке от -3 до +3 с шагом 0,1. В итоге вы получите 60 значений, по которым график функции будет проложен весьма плавно.
3. Далее, в ячейку C3 забьём формулу функции синуса или ту, которую вам надо построить. Если помните тригонометрию, то функция синуса записывается в виде y = sin x.
4. Однако формулы в Excel отличаются от записей математических формул, и всегда начинаются со знака равно — «=». В нашем примере, вы должны записать в ячейке C3 формулу вида = SIN(B3).
5. Забивать формулу в каждой новой строке очень долго и неудобно (представляете, нужно вбить 60 раз!). Для того чтобы формула была в каждой ячейке необходимо «протянуть» формулу из первой ячейки на все остальные. При этом ссылка на ячейку, откуда берётся значение аргумента будет смещаться построчно.
6. Для этого щёлкаем на ячейке с набранной формулой. В правом нижнем углу ячейки должен появиться небольшой квадратик. Следует навести на него курсор мышки, и когда квадратик превратится в крестик, нажимаем правую кнопку и копируем «протягиванием» формулу вниз на нужное количество ячеек.
7. Переходим к построению графика функции. Заходим в Меню «Вставка» -> «Диаграмма» и выбираем подходящую точечную диаграмму. Жмем волшебную кнопку .
8. В открывшемся окне щелкаем вкладку «Ряд». Добавляем ряд нажатием кнопки .
9. В этом окне нужно задать, из какого диапазона будут выбраны числа для графика. Чтобы выбрать нужные ячейки, следует щёлкнуть поочередно по кнопкам.
10. После этого выделим те ячейки, откуда будут выбраны значения для x и y.
11. Последним шагом станет нажатие кнопки .

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

• если k > 0, то график наклонен вправо;
• если k < 0, то график наклонен влево.

Коэффициент b отвечает за сдвиг графика вдоль оси OY:

• если b > 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
• если b < 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вниз вдоль оси OY.

Начертим три графика функции: y = 2x + 3, y = 1/₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = -1/₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

• график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
• график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
• график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k < 0 и b > 0, то график функции y = kx + b выглядит так:

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

Если k > 0 и b < 0, то график функции y = kx + b выглядит так:

Если k < 0 и b < 0, то график функции y = kx + b выглядит так:

Если k = 0, то функция y = kx + b преобразуется в функцию y = b. В этом случае ординаты всех точек графика функции равны b. А график выглядит так:

Если b = 0, то график функции y = kx проходит через начало координат. Так выглядит график прямой пропорциональности:

На уроках математики в Skysmart ученики рисуют такие графики вместе с учителем на интерактивной онлайн-доске. Преподаватель видит ход мысли ученика и сразу может помочь взглянуть по-другому, если что-то не получается с первого раза. Запишите ребенка на бесплатный вводный урок и попробуйте сами.

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции. Например, график уравнения х = 3:

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ * k₂ = -1 или k₁ = -1/_k2.

Точки пересечения графика функции y = kx + b с осями координат:

• С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
  Координаты точки пересечения с осью OY: (0; b).
• С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = -b/_k.
  Координаты точки пересечения с осью OX: (-b/_k; 0)

Неизбежная окружность

У окружности есть синус. Да. Но увидеть синус внутри окружности — это всё равно, что получить из омлета яйца обратно, когда все они хорошенько друг с другом перемешаны!

Давайте помедленнее. В симуляторе установите такие параметры: vertical:none и horizontal: sine*. Видите, как смайлик движется вперёд-назад? Это и есть движение синуса. Небольшой фокус: обычно синус начинает свой цикл на нейтральной срединной точке и бежит к максимуму. На этот раз мы начинаем в максимуме и падаем к срединной точке. Синус, который «стартует на максимуме», называется косинусом, и это просто версия синуса (как горизонтальная прямая является версией вертикальной прямой)

Настало время для обеих синусных волн: установите параметры vertical:sine и horizontal:sine*. И… у нас получилась окружность!

Горизонтальные и вертикальные «прыжки» в сумме дали круговое движение. В большинстве учебников рисуют окружность и пытаются извлечь из нее синус, но я предпочитаю обратный подход: начать с простого горизонтального или вертикального движения и добавить противоположное.

Строим график функции, заданный системой уравнений, в MS EXCEL

Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.

Пусть дана система уравнений

Требуется на отрезке  построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.

Решение (1 ряд данных)

Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.

СОВЕТ: О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL. О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL.

Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1):

Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.

Чтобы построить диаграмму типа Точечная:

• выделите любую ячейку таблицы;
• во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами.

Чтобы построить диаграмму типа График:

• выделите любую столбец f(x) вместе с заголовком;
• во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами.

У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных.

Решение (2 ряда данных)

Создадим другую таблицу с исходными данными в файле примера, лист График:

Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола.

Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы.

При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.

У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График.

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Топологии для формирования синусоидального сигнала

следующим образом

Плюсы:

• Минимально возможное количество силовых транзисторов, а значит потери в 2 раза меньши и стоимость устройства тоже ниже
• Сквозной ноль. Это упрощает процесс сертификации, особенно CE и ATEX. Связано это с тем, что сквозной ноль позволяет системам защиты по входу (например, УЗО) срабатывать так же при возникновение аварии в выходных цепях после преобразователя
• Простая топология, что позволяем максимально уменьшить стоимость изделия при мелко-
  и средне серийном производстве

Минусы:

• Необходимость двухполярного источника питания. Как видите на схему инвертора надо подавать ±380В и еще ноль
• Удвоенное количество высоковольтных конденсаторов. Высоковольтные конденсаторы большой емкости и с малым ESR на мощностях от 3-4 кВт начинают составлять от 20 до 40%
  стоимости компонентов
• Применение электролитических конденсаторов в «делителе». Они сохнут, подобрать конденсаторы с одинаковыми параметрами практически нереально, а если учесть, что параметры электролитов меняются в процессе эксплуатации, то и бессмысленно. Заменить на пленку можно, но дорого

Плюсы:

• Очень высокая надежность. Она в основном обусловлена качеством системы управления силовыми транзисторами и не зависит от деградации компонентов
• Входная емкость требуется в разы, а то и на порядок меньше. Необходимо лишь обеспечить расчетное значение ESR. Это позволяет использовать пленочные конденсаторы при сохранение себестоимости. Пленочные конденсаторы — не сохнут, лучше ведут в суровых температурах, рабочий ресурс на порядок выше, чем у электролитов
• Минимальные пульсации напряжения на транзисторах, а значит можно применить транзисторы на меньшее напряжение
• Простота и понятность алгоритмов работы. Это приводит к значительному уменьшению времени на разработку изделия, а также на его пуско-наладочные работы

Минусы:

• Увеличенное количество силовых транзисторов, а значит необходимо более серьезное охлаждение. Увеличение цены на транзисторах, но за счет меньшего количества конденсаторов это скорее даже плюс
• Повышенная сложность драйвера, особенно при требованиях к наличию гальванической развязки

Небольшой итог

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

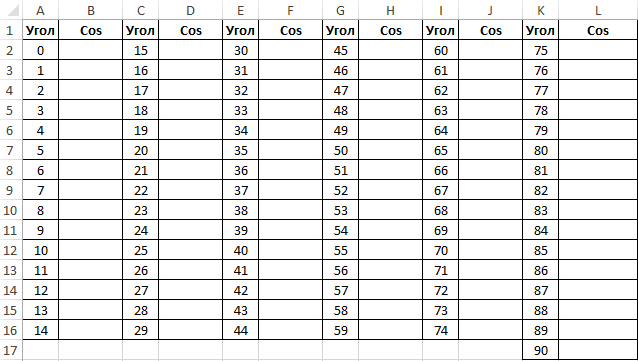
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

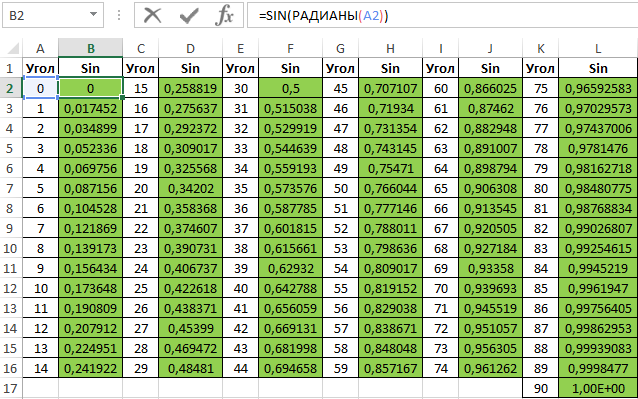
Вычислим значения для всех значений углов. Полученный результат:

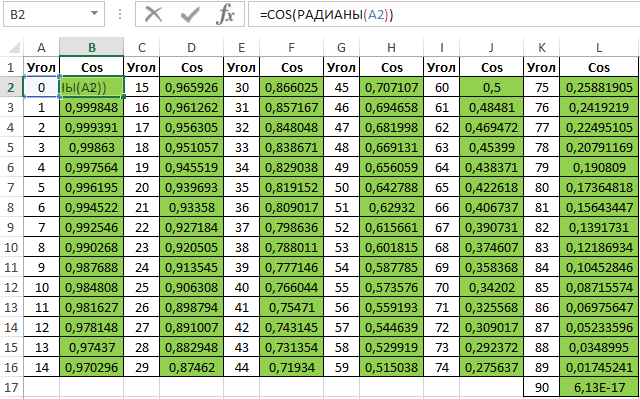Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Вычисление значения арктангенса

Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.

Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:

Способ 1: ручной ввод функции

Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.

1. Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:

   Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:

   Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.

2. Для вывода результатов расчета на экран нажимаем на кнопку Enter.

Способ 2: вычисление при помощи Мастера функций

Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.

1. Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
2. Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».

3. После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».

   Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».

4. После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.

Урок: Мастер функций в Excel

Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Да Нет

Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.

В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов. Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.

Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы. И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.

Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:

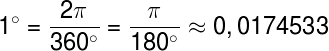В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот. Давайте подробно остановимся на особенностях применения каждой из них.