График линейной функции, его свойства и формулы

Точка пересечения двух прямых в пространстве

Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)

Пример 6. Найти точку пересечения прямых — 1 = — 1 = — 1 и — 3-2 = 2 — = .

Решение: Составим систему уравнений

— 1 = — 1 = — 1 = — 3-2 = 2 — = =
  =>  
= + 1 = + 1 = + 1 — 3-2 = 2 — = =
  =>  

Подставим значения , , из 1, 2, 3 уравнений в 4, 5, 6 уравнения

= + 1 = + 1 = + 1 + 1 — 3-2 = 2 — ( + 1) = + 1 =
  =>  
= + 1 = + 1 = + 1 — 2-2 = 1 — = + 1 =

К шестому уравнению добавим пятое уравнение

= + 1 = + 1 = + 1 — 2-2 = 1 — = + 1 + (1 — ) = +
  =>  
= + 1 = + 1 = + 1 — 2-2 = 1 — = = 1

Подставим значение в четвертое и пятое уравнения

= + 1 = + 1 = + 1 — 2-2 = 11 — = 1 = 1
  =>  
= + 1 = + 1 = + 1 — 2 = -2 = 0 = 1
  =>  

= + 1 = + 1 = + 1 = 0 = 0 = 1
  =>  
= 0 + 1 = 1 = 0 + 1 = 1 = 0 + 1 = 1 = 0 = 0 = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.

Пример 7. Найти точку пересечения прямых = 2 — 3 = = — + 2 и = + 1 = 3 — 2 = 3.

Решение: Составим систему уравнений заменив во втором уравнении параметр на

= 2 — 3 = = — + 2 = + 1 = 3 — 2 = 3

Подставим значения , , из 1, 2, 3 уравнений в 4, 5, 6 уравнения

= 2 — 3 = = — + 22 — 3 = + 1 = 3 — 2- + 2 = 3
  =>  
= 2 — 3 = = — + 22 = + 4 = 3 — 2 = -1
  =>  

Подставим значение из шестого уравнения в остальные уравнения

= 2·(-1) — 3 = (-1) = -(-1) + 22·(-1) = + 4-1 = 3 — 2 = -1
  =>  
= -5 = -1 = 3 = -6 = 13 = -1

Ответ. Так как -6 ≠ 13, то прямые не пересекаются.

Типы графиков

Помимо того что в MathCAD определены быстрые графики, которые вызываются с помощью горячих клавиш, существуют и другие графические приложения. Например, пользователь может в шапке программы найти раздел «Вставка», а в ней — подраздел «График», в котором можно просмотреть все доступные графики в «Маткаде»:

• График X-Y — показывает зависимость одной величины от другой. Самый распространенный тип, который позволяет быстро оценить и исследовать зависимости.
• Полярный график — использует полярные координаты. Суть графика — показать зависимость одной переменной от другой только в полярной координатной плоскости.
• График поверхности — создает поверхность в пространстве.
• Векторное поле, 3-D график разброса, столбчатая 3-D диаграмма используются для других специальных целей.

Строим графики с точками пересечений

Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

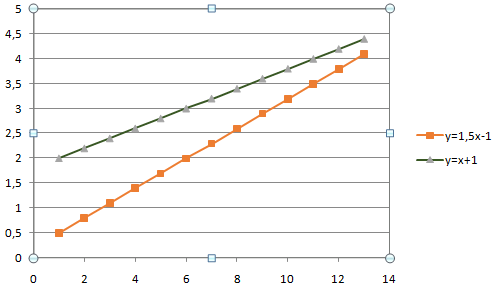
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.

Строим графики с точками пересечений

Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

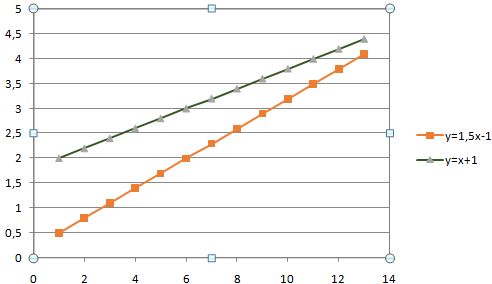
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.

Инструкция

• Любой график можно задать определенной функцией. Для того чтобы найти те точки, в которых графики пересекаются, нужно решить уравнение, которое имеет вид: f₁(x)=f₂(x). Результат решения и будет той точкой (или точками), которые вы ищете. Рассмотрите следующий пример. Пусть значение y₁=k₁x+b₁, а значение y₂=k₂x+b₂. Для нахождения точек пересечения на оси абсцисс необходимо решить уравнение y₁=y₂, то есть k₁x+b₁=k₂x+b₂.
• Преобразуйте данное неравенство, получив k₁x-k₂x=b₂-b₁. Теперь выразите x: x=(b₂-b₁)/(k₁-k₂). Таким образом вы найдете точку пересечения графиков, которая находится по оси OX. Найдите точку пересечения на оси ординат. Просто подставьте в какую-либо из функций значение x, которое вы нашли ранее.
• Предыдущий вариант подходит для линейной функции графиков. Если же функция квадратичная, воспользуйтесь следующими инструкциями. Таким же способом, как и с линейной функцией, найдите значение x. Для этого решите квадратное уравнение. В уравнении 2x² + 2x — 4=0 найдите дискриминант (уравнение дано для примера). Для этого используйте формулу: D= b² – 4ac, где b – значение перед X, а c – это числовое значение.
• Подставив числовые значения, получите выражение вида D= 4 + 4*4= 4+16= 20. От значения дискриминанта зависят корни уравнения. Теперь к значению переменной b со знаком «-» прибавьте или отнимите (по очереди) корень из полученного дискриминанта, и поделите на удвоенное произведение коэффициента a. Так вы найдете корни уравнения, то есть координаты точек пересечения.
• Графики квадратичной функции имеют особенность: ось OX будет пересекаться два раза, то есть вы найдете две координаты оси абсцисс. Если вы получите периодическое значение зависимости X от Y, тогда знайте, что график пересекается в бесконечном количестве точек с осью абсцисс. Проверьте, правильно ли вы нашли точки пересечения. Для этого подставьте значения X в уравнение f(x)=0.

Случай двух нелинейных функций

Пример 3

Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $

Решение

Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2\cdot 0 + 1 = 1 $$ $ M (0;1) $ — точка пересечения графиков функций

Ответ

$$ M (0;1) $$

Два графика на координатной плоскости, если они не параллельны, обязательно пересекаются в какой-либо точке. И нередко в алгебраических задачах такого типа требуется найти координаты данной точки. Поэтому знание инструкций по ее нахождению принесет большую пользу как школьникам, так и студентам.

Находим точку пересечения графиков в Excel

В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ.
Найти общие значения в рядах данных для указанных функций.

В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

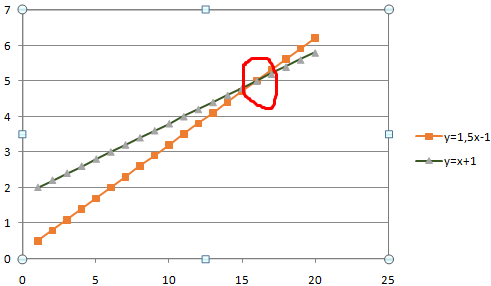
Второй способ.
Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

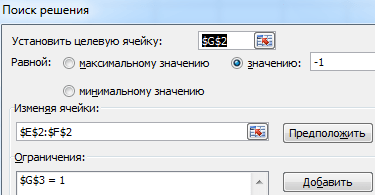
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Строим графики с точками пересечений

Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.

Случай двух линейных функций

Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.

Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 \neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ — это коэффициент угла наклона. Если $ k_1 \neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.

Пример 1

Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций.

Решение

Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 \neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x — x = 3+5 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2\cdot 8 — 5 = 16 — 5 = 11 $$ Итак, $ M (8;11) $ — является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M (8;11) $$

Случай двух нелинейных функций

Пример 3

Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $

Решение

Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2\cdot 0 + 1 = 1 $$ $ M (0;1) $ — точка пересечения графиков функций

Ответ

$$ M (0;1) $$

В двумерном пространстве две прямые пересекаются только в одной точке, задаваемой координатами (х,y). Так как обе прямые проходят через точку их пересечения, то координаты (х,y) должны удовлетворять обоим уравнениям, которые описывают эти прямые. Воспользовавшись некоторыми дополнительными навыками вы сможете находить точки пересечения парабол и других квадратичных кривых.

Пример решения

Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:

Приравнять уравнения: 2t+7=t-1.
Перенести переменные влево, а константы — вправо: 2t-t=-1-7.
Привести подобные коэффициенты: t=-8.
Найти координаты второй составляющей: z=-8-1=-9.
Искомая точка пересечения: (-8;-9).

В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.

Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.

Предыдущая
АлгебраДеление многочлена на многочлен – правило и примеры
Следующая
АлгебраНеполное квадратное уравнение — виды, примеры и способы решения

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Проще всего освоить такой материал на веселых задачках — в детской школе Skysmrt подобрали тысячи интерактивных упражнений разной сложности, чтобы ребенок нагнал упущенное и повысил оценки в школе без давления и суеты.

Приходите на бесплатный вводный урок математики: покажем, как все устроено и вдохновим на учебу.

Решение

Шаг 1

Для начала обратим внимание, что исходный тип диаграммы – График с маркерами

Ряды этого типа описываются так:

Заметьте, что тут нет значений координат по оси X, а есть только координаты по условной оси Y. Этим подразумевается, что условная ось X – общая для всех рядов, а также, что при их построении не используются значения, отличные от заранее фиксированного ряда оси X. Вот есть у нас периоды: 1, 2, 3 и т.д., нанесенные на ось Х, и использовать можно только их. Периода, где X=3.5 не существует для данного типа диаграммы.

Однако, нам для решения этой задачи необходимо, чтобы мы могли задавать любое значение X, в том числе промежуточные, так как наши линии как раз пересекаются где-то «между периодами». Поэтому тип диаграммы мы меняем для всех рядов с » графика с маркерами » на » точечную с прямыми отрезками и маркерами «.

Следует упомянуть, что наш случай осложняется наличием двух вертикальных осей: основной и вспомогательной, так как значения расхода материала и объёма производства сильно друг от друга отличаются.

Шаг 2

Теперь нам необходимо нанести на диаграмму дополнительные ряды данных:

Точки пересечения линий расхода материала с нормами расхода. Таких точек у нас будет 3, исходя из условий примера. Эти точки нам необходимо будет расчитать, вспомнив школьный курс геометрии (см. лист Треугольники ). В файле учебного примера на листе После в таблице N3:Q5 мы получили координаты нужных точек путем нехитрых формул. Тип диаграммы Точечная в отличие от рядов с показателями работы производства.

Точки пересечения найденных значений по оси X с объемом производства. Расчитывается в таблице N8:Q10 по близким формулам. Тип диаграммы Точечная .

Пунктирные линии, которые мы рисуем из эстетических соображений. Таблица с их координатами находится в N12:P18 .

Добавляем ряды данных в соответствии с теми точками, которые мы расчитали. Щёлкните ПКМ по диаграмме и выберите » Выбрать данные. «, далее воспользуйтесь кнопкой » Добавить «.

Пример одного из рядов:

Находим точку пересечения графиков в Excel

В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ.
Найти общие значения в рядах данных для указанных функций.

В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

Второй способ.
Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

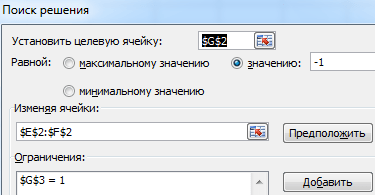
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Точки пересечения для трех показателей

Существует три показателя, которые измерялись во времени.

По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).

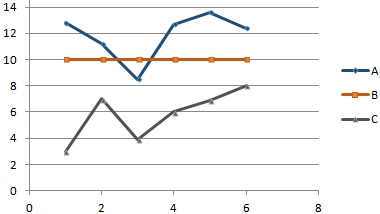
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.

Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:

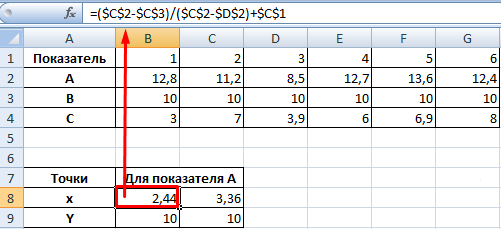
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.

Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:

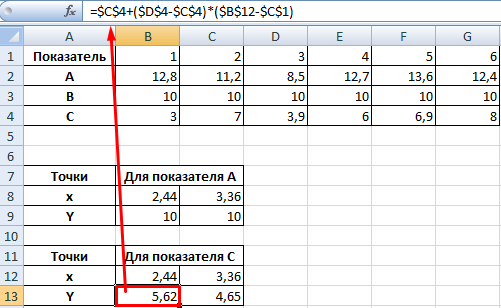
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).

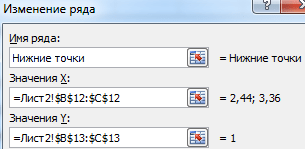
Получается такой рисунок:

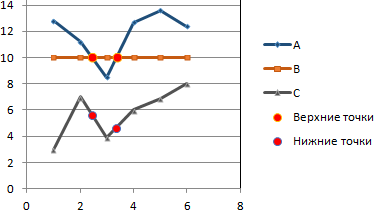
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:

Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.

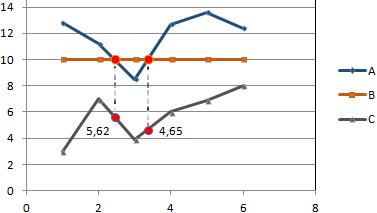
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.

1. Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
2. Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
3. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.

Точка пересечения двух прямых на плоскости

Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:

• графический
• аналитический

Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.

Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

Пример 1. Найти точку пересечения прямых  = 2 — 1 и  = -3 + 1.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

= 2 — 1 = -3 + 1

Вычтем из первого уравнения второе

— = 2 — 1 — (-3 + 1) = -3 + 1     =>    
0 = 5 — 2 = -3 + 1

Из первого уравнения найдем значение

5 = 2 = -3 + 1     =>    
= 25 = 0.4 = -3 + 1

Подставим значение во второе уравнение и найдем значение

= 0.4 = -3·(0.4) + 1 = -1.2 + 1 = -0.2

Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

Пример 2. Найти точку пересечения прямых  = 2 — 1 и = 2 + 1 = .

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

= 2 — 1 = 2 + 1 =

В первое уравнение подставим значения и из второго и третьего уравнений.

= 2·(2 + 1) — 1 = 2 + 1 =     =>    
= 4 + 1 = 2 + 1 =     =>    

-3 = 1 = 2 + 1 =     =>    
= -13 = 2 + 1 =

Подставим значение во второе и третье уравнение

= -13 = 2·(-13) + 1 = -23 + 1 = 13 = -13

Ответ. Точка пересечения двух прямых имеет координаты (13, -13)

Пример 3 Найти точку пересечения прямых 2 + 3 = 0 и — 23 = 4.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

2 + 3 = 0 — 23 = 4

Из второго уравнения выразим через

2 + 3 = 0 = 4· — 23

Подставим в первое уравнение

2 + 3·4· — 23 = 0 = 4· — 23     =>    
2 + 4·( — 2) = 0 = 4· — 23     =>    

2 + 4 — 8 = 0 = 4· — 23     =>    
6 = 8 = 4· — 23     =>    

= 86 = 43 = 4· — 23     =>    
= 86 = 43 = 4·4/3 — 23 = 4·-2/3 3 = -89

Ответ. Точка пересечения двух прямых имеет координаты (43, -89)

Пример 4. Найти точку пересечения прямых  = 2 — 1 и  = 2 + 1.

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как ₁ = ₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

= 2 — 1 = 2 + 1

Вычтем из первого уравнения второе

— = 2 — 1 — (2 + 1) = -3 + 1     =>    
0 = -2 = -3 + 1

В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).

Ответ. Прямые не пересекаются (прямые параллельны).

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

• если k > 0, то график наклонен вправо;
• если k < 0, то график наклонен влево.

Коэффициент b отвечает за сдвиг графика вдоль оси OY:

• если b > 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
• если b < 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вниз вдоль оси OY.

Начертим три графика функции: y = 2x + 3, y = 1/₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = -1/₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

• график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
• график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
• график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k < 0 и b > 0, то график функции y = kx + b выглядит так:

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

Если k > 0 и b < 0, то график функции y = kx + b выглядит так:

Если k < 0 и b < 0, то график функции y = kx + b выглядит так:

Если k = 0, то функция y = kx + b преобразуется в функцию y = b. В этом случае ординаты всех точек графика функции равны b. А график выглядит так:

Если b = 0, то график функции y = kx проходит через начало координат. Так выглядит график прямой пропорциональности:

На уроках математики в Skysmart ученики рисуют такие графики вместе с учителем на интерактивной онлайн-доске. Преподаватель видит ход мысли ученика и сразу может помочь взглянуть по-другому, если что-то не получается с первого раза. Запишите ребенка на бесплатный вводный урок и попробуйте сами.

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции. Например, график уравнения х = 3:

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ * k₂ = -1 или k₁ = -1/_k2.

Точки пересечения графика функции y = kx + b с осями координат:

• С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
  Координаты точки пересечения с осью OY: (0; b).
• С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = -b/_k.
  Координаты точки пересечения с осью OX: (-b/_k; 0)

Построение графика функции

Невозможно научиться работать с вычислительной средой без примеров, поэтому будем разбираться в MatchCAD на шаблоне.

Допустим, задана функция f(x) = (e^x/(2x-1)^2)-10 в интервале , которую необходимо построить и провести исследование. Прежде чем приступить к построению графика функции, необходимо данную функцию перевести в математический вид в самой программе.

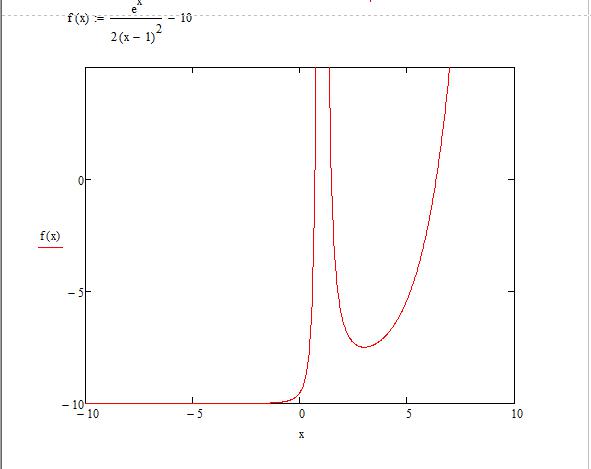
1. После того как функция была задана, следует вызвать окно быстрого графика клавишей Shift + 2. Появляется окошечко, в котором расположены 3 черных квадратика по вертикали и горизонтали.
2. По вертикали: самый верхний и нижний отвечают за интервалы значений, которые можно регулировать, средний задает функцию, по которой пользователь может построить график в «Маткаде». Крайние черные квадратики оставляем без изменения (значения автоматически присвоятся после построения), а в средний пишем нашу функцию.
3. По горизонтали: крайние отвечают за интервалы аргумента, а в средний нужно вписать «х».
4. После проделанных шагов нарисуется график функции.

Методики нахождения точек

Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными

В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида

Первой и второй степени

Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:

Раскрыть скобки и привести подобные коэффициенты.
Выполнить перенос известных в одну, а неизвестных — в другую часть равенства.
Произвести необходимые математические преобразования.
Найти корень.

Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

Разложить на множители.
Выделить полный квадрат.
Найти дискриминант.
По теореме Виета.

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д<0, искомое тождество с неизвестными вообще не имеет решений. Определить значение корней возможно по таким соотношениям: t1=[-S-(Д)^(1/2)]/2P и t2=[-S+(Д)^(1/2)]/2P, где t1 и t2 — точки пересечения с осью абсцисс.

Если коэффициент при второй степени (P) эквивалентен 1, то дискриминант можно не высчитывать, а воспользоваться сокращенным вариантом решения — теоремой Виета. Суть ее заключается в подборе корней по таким формулам: t1+t2=-S и t1*t2=U. Иногда для реализации этой методики нужно сократить обе части на коэффициент Р. Алгоритм решения квадратных уравнений имеет следующий вид:

Выполнить при необходимости различные алгебраические преобразования (раскрыть скобки и привести подобные слагаемые).
Выбрать один из способов решения и реализовать его.
Проверить корни, подставив их в исходное выражение.

Следует отметить, что распространенная ошибка новичков — отсутствие проверки. В результате неправильных действий образуются ложные корни, а оценка на контрольной, зачете или экзамене существенно снижается.

https://youtube.com/watch?v=TPZoy2M_2mo

Кубические и биквадратные

Решение тождеств кубического и биквадратного типов с неизвестными осуществляется двумя способами. К ним относятся:

Понижение степени (разложение на множители).
Замена переменной.

В первом случае необходимо выполнить преобразования, которые позволят применить одну из формул сокращенного умножения. Однако этот метод применяется довольно редко, поскольку математики отдают предпочтение второму способу. Для его реализации вводится дополнительная переменная, обладающая более низкой степенью и существенно упрощающая выражение. Алгоритм имеет такой вид:

Выполняются необходимые математические преобразования.
Выражается переменная через другую.
Решается квадратное или линейное уравнение.
Промежуточные корни, полученные в третьем пункте алгоритма, подставляются во второй.
Вычисляются искомые корни.
Осуществляется проверка.
Отсеиваются ложные решения, и записывается ответ.

Для проверки рекомендуется воспользоваться онлайн-приложениями, позволяющими вычислить корни, а также построить графики функций. Кроме того, для кубического многочлена Pt 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:

Уравнение требуется разделить на P.
Осуществить замену: t=m-(S/(3P)). При этом получается тождество вида m^3 +km+l=0.
Найти значение коэффициентов по формулам: k= / (27P 3 ) и l=[(3PU-S 2 )/(3P 2 )]. Подставить их во второй пункт и найти промежуточные корни, при помощи которых найти основные значения переменных.

Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.