Калькулятор python, принимающий строковый ввод
Содержание:
- Не все так гладко…
- 1.5 Переменные
- Вычисления
- Память
- Исходный код
- Подсказки типов | Ожидание типа | Type hinting (Python 3.5+)
- Написание простейшего калькулятора в Python 3
- Консольный калькулятор на Python:
- Часть вторая: создаем GUI для программы
- Написание калькулятора на Python
- 1.4 Операторы присваивания
- Знак равно
- Текущая операция (current_op)
- Pathlib (Python 3.4+)
- 1.2 Вывод
Не все так гладко…
Однако, не все так гладко в python. Например, сейчас уживается две версии языка 2. и 3., обе они развиваются параллельно, однако синтаксис 2ой версии не совместим полностью с синтаксисом 3ей версии.
Еще одна проблема может возникнуть у вас, если вы не обладатель linux, в этом случае при установке ряда библиотек у вас могут возникнуть трудности, некоторые библиотеки будут полностью не совместимы, например tensorflow.
P.S: все библиотеки для python, о которых говорилось данной статье, имеют открытый исходный код и распространяются бесплатно. Для их загрузки можно воспользоваться командой pip или просто скачать сборку Anaconda, которая содержит все основные библиотеки.
1.5 Переменные
Переменные начинаются с маленькой буквы
Имена переменных должны начинаться с маленькой буквы латинского алфавита.
Переменные могут начинаться
с заглавной буквы или знака подчёркивания, но это особые случаи,
которые не следует использовать на постоянной основе. После первой
маленькой буквы, переменные могут включать в себя как заглавные,
так и маленькие буквы, вперемешку с числами и знаками подчёркивания.
Переменные не могут содержать пробелы.
Переменные чувствительны к регистру символов. Это может сбить с толку, если программист
не ожидает этого. В коде внизу, на экран будет выведено 6, а не 5, потому что x и X —
это две разные переменные.
x=6 X=5 print(x)
| Дозволенные имена переменных | Запрещённые имена переменных | Дозволенные, но не правильные |
|---|---|---|
|
distance first_name ds9 |
9ds first name %correct |
FirstName X LIVES_LEFT |
Вычисления
Вычисления пределов
Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно . Например, если вы хотите вычислить предел функции , где , то надо написать .
sym.limit(sym.sin(x) / x, x, 0) # результат 1
Также можно вычислять пределы, которые стремятся к бесконечности.
sym.limit(x, x, sym.oo) # результат oo sym.limit(1 / x, x, sym.oo) # результат 0 sym.limit(x ** x, x, 0) # результат 1
Дифференцирование
Для дифференцирования выражений в есть функция . Ниже даны примеры ее работы.
sym.diff(sym.sin(x), x) # результат cos(?) sym.diff(sym.sin(2 * x), x) # результат 2cos(2?) sym.diff(sym.tan(x), x)
Проверим результат последней функции при помощи определения производной через предел.
sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)
Результат тот же.
Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: . Ниже приведено несколько примеров.
sym.diff(sym.sin(2 * x), x, 1) # результат 2cos(2?) sym.diff(sym.sin(2 * x), x, 2) # результат −4sin(2?) sym.diff(sym.sin(2 * x), x, 3) # результат −8cos(2?)
Разложение в ряд
Для разложения выражения в ряд Тейлора используется следующий синтаксис: .
sym.series(sym.cos(x), x)
sym.series(1/sym.cos(x), x)
Интегрирование
В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции . Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:
sym.integrate(sym.sin(x), x) # результат −cos(?) sym.integrate(sym.log(x), x) # результат ?log(?)−?
Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:
sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)
Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.
sym.integrate(x**3, (x, -1, 1)) # результат 0 sym.integrate(sym.sin(x), (x, 0, sym.pi / 2)) # результат 1 sym.integrate(sym.cos(x), (x, -sym.pi / 2, sym.pi / 2)) # результат 2
Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).
sym.integrate(sym.exp(-x), (x, 0, sym.oo)) # результат 1
Решение уравнений
При помощи можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция .
sym.solveset(x ** 4 - 1, x) # результат {−1,1,−?,?}
Как можно заметить, первое выражение функции приравнивается к и решается относительно . Также возможно решать некоторые уравнения с трансцендентными функциями.
sym.solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}
Системы линейных уравнений
способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции , которая используется для таких задач.
solution = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y)) solution, solution # результат (-3, 1)
Факторизация
Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в предусмотрена функция , которая способна производить факторизацию очень широкого класса полиномов.
f = x ** 4 - 3 * x ** 2 + 1 sym.factor(f)
sym.factor(f, modulus=5)
Булевы уравнения
Также в реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция .
sym.satisfiable(x & y) # результат {x: True, y: True}
Данный результат говорит нам о том, что выражение будет истинным тогда и только тогда, когда и истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат .
sym.satisfiable(x & ~x) # результат False
Память
Наконец, мы можем определить обработчики для действий памяти. Для «Calculon» мы подобрали только два действия с памятью – хранение и повторный вызов. Хранение берет текущее значение с LCD дисплея и копирует его в self.memory. Повторный вызов берет значение из self.memory и помещает его в конечное место нашего стека.
Python
def memory_store(self):
self.memory = self.lcdNumber.value()
def memory_recall(self):
self.state = INPUT
self.stack = self.memory
self.display()
|
1 |
defmemory_store(self) self.memory=self.lcdNumber.value() defmemory_recall(self) self.state=INPUT self.stack-1=self.memory self.display() |
Настроив режим на INPUT и обновив дисплей мы сможем действовать также, как при введении чисел от руки.
Исходный код
Скачать: https://github.com/mfitzp/15-minute-apps/tree/master/calculator
Полный исходный код Calculon доступен в пятнадцатиминутном репозитории. Вы можете скачать\клонировать его для получения рабочей копии:
Shell
git clone git@github.com:mfitzp/15-minute-apps.git
cd 15-minute-apps/calculator
|
1 |
git clonegit@github.commfitzp15-minute-apps.git cd15-minute-appscalculator |
Затем установить все необходимые зависимости при помощи:
Shell
pip3 install -r requirements.txt
| 1 | pip3 install-rrequirements.txt |
После этого вы можете запустить калькулятор при помощи:
Shell
python3 notepad.py
| 1 | python3 notepad.py |
Ознакомьтесь с тем, как работает код в путеводителе.
Подсказки типов | Ожидание типа | Type hinting (Python 3.5+)
Спор о том, какое лучше — статическое или динамическое — не умолкают и по сей день и у каждого есть свое мнение на этот счет. Это личное дело читателя — когда ему нужно вписывать типы, но мне кажется что вы как минимум должны знать о том, что Python 3 поддерживает .
Python
def sentence_has_animal(sentence: str) -> bool:
return «animal» in sentence
print(sentence_has_animal(«У Ивана есть своя собственная Bitcoin ферма»)) # True
|
1 |
defsentence_has_animal(sentencestr)->bool return»animal»insentence print(sentence_has_animal(«У Ивана есть своя собственная Bitcoin ферма»))# True |
Написание простейшего калькулятора в Python 3
Язык программирования Python является отличным инструментом для обработки чисел и математических выражений. На основе этого качества можно создавать полезные программы.
В данном руководстве вам предлагается полезное упражнение: попробуйте написать простую программу командной строки для выполнения вычислений. Итак, в данном руководстве вы научитесь создавать простейший калькулятор в Python 3.
В руководстве используются математические операторы, переменные, условные выражения, функции.
Требования
Для выполнения руководства нужно установить Python 3 на локальную машину и развернуть среду разработки. Все необходимые инструкции можно найти здесь:
- Настройка локальной среды разработки для Python 3 в CentOS 7
- Настройка локальной среды разработки для Python 3 в Windows 10
- Настройка локальной среды разработки для Python 3 в Mac OS X
- Настройка локальной среды разработки для Python 3 в Ubuntu 16.04
Консольный калькулятор на Python:
Как говорилось выше, мы сделаем легкий калькулятор на Python, и для этого нам нужно создать только один Python файл, я его назову «main.py».
Внутри него создадим функцию которая будет за всё отвечать, вот примерно так:
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# Создание функции defmain() # Выводим сообщение print(«Это простой калькулятор на Python») # Запускаем бесконечный цикл whileTrue # Выводим сообщение какие действия есть print(«Выберите действие которое хотите сделать:\n» «Сложить: +\n» «Вычесть: -\n» «Умножить: *\n» «Поделить: /\n» «Выйти: q\n») # Переменная для хранения действия action=input(«Действие: «) # Если action равен q то ifaction==»q» # Выводим сообщение print(«Выход из программы») # Выходим из цикла break # Если action равен +, -, *, /, то ifaction in(‘+’,’-‘,’*’,’/’) # Присваиваем значение переменной x x=float(input(«x = «)) # Присваиваем значение переменной y y=float(input(«y = «)) # Если action равен + то ifaction==’+’ # Выводим сумму x и y print(‘%.2f + %.2f = %.2f’%(x,y,x+y)) # Если action равен — то elifaction==’-‘ # Выводим разность x и y print(‘%.2f — %.2f = %.2f’%(x,y,x-y)) # Если action равен * то elifaction==’*’ # Выводим результат умножения x на y print(‘%.2f * %.2f = %.2f’%(x,y,x*y)) # Если action равен / то elifaction==’/’ # Если y не равен нулю то ify!= # Выводим результат деления x на y print(‘%.2f / %.2f = %.2f’%(x,y,xy)) else# Иначе # Выводим сообщение, что на ноль делить нельзя print(«Деление на ноль!») |
То есть мы создаём функцию где происходит вся логика, внутри неё первым делом выводим сообщение, что мы открыли калькулятор.
Потом запускаем бесконечный цикл и в нём даём выбрать действие, тут как обычно, то есть, если выбираем знак плюса, то будем складывать и т.д..
После идёт проверка команд, если выбрать кнопку «q», то выходим из программы, если же это арифметический знак, то вводим два числа, кладём их в переменные в формате числа с плавающей точкой.
Потом проверяем конкретный знак, зависимо от него и делаем действии, выводим на экран, самое интересное это с делением, мы делаем проверку, если делитель, то есть «y», равен нулю то тогда не будем делить.
Последние что осталось это объявить переменную, вот:
Python
|
1 2 |
if__name__==’__main__’ main() |
Теперь запускаем файл, для этого переходим в папку и используем эту команду:
PowerShell
| 1 | python3 main.py |
Должно быть что-то типа этого:

Как видите наш консольный калькулятор на Python готов, в целом всё очень просто.
Часть вторая: создаем GUI для программы
Для простоты будем создавать GUI встроенными средствами Python, поэтому импортируем все из библиотеки Tkinter:
from Tkinter import *
В Python версии 3.х название модуля следует писать с маленькой буквы — tkinter.
Далее создаем само окно и размещаем на нем необходимые виджеты:
# родительский элемент
root = Tk()
# устанавливаем название окна
root.title("Quadratic calculator")
# устанавливаем минимальный размер окна
root.minsize(325,230)
# выключаем возможность изменять окно
root.resizable(width=False, height=False)
# создаем рабочую область
frame = Frame(root)
frame.grid()
# поле для ввода первого аргумента уравнения (a)
a = Entry(frame, width=3)
a.grid(row=1,column=1,padx=(10,0))
# текст после первого аргумента
a_lab = Label(frame, text="x**2+").grid(row=1,column=2)
# поле для ввода второго аргумента уравнения (b)
b = Entry(frame, width=3)
b.grid(row=1,column=3)
# текст после второго аргумента
b_lab = Label(frame, text="x+").grid(row=1, column=4)
# поле для ввода третьего аргумента уравнения (с)
c = Entry(frame, width=3)
c.grid(row=1, column=5)
# текст после третьего аргумента
c_lab = Label(frame, text="= 0").grid(row=1, column=6)
# кнопка решить
but = Button(frame, text="Solve").grid(row=1, column=7, padx=(10,0))
# место для вывода решения уравнения
output = Text(frame, bg="lightblue", font="Arial 12", width=35, height=10)
output.grid(row=2, columnspan=8)
# запускаем главное окно
root.mainloop()
Если вы в точности повторили указанный код, то после запуска скрипта у вас получится примерно следующее окно:
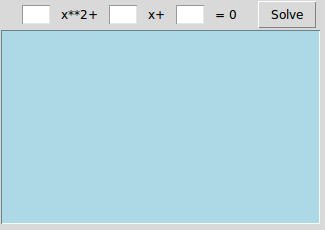
Отлично, программа работает. Осталось объяснить Python как связать эти две части.
Написание калькулятора на Python
Сделать простой калькулятор в Python для выполнения основных математических операций, таких как сложение, вычитание, умножение и деление двух чисел, введенных пользователем. Чтобы сделать калькулятор на python, сначала предоставьте 5 вариантов пользователю, пятый вариант для выхода. После предоставления всех пяти опций пользователю, попросите пользователя ввести его / ее выбор и выполнить желаемую операцию, как показано в программе, приведенной ниже.
Код программирования Python для создания калькулятора
Следующая программа на Python предоставляет пользователю опции и просит ввести его / ее выбор для выполнения и показать желаемый результат в качестве вывода:
# Программа Python — создайте простой калькулятор
# Python Program - Make Simple Calculator
print("1. Addition");
print("2. Subtraction");
print("3. Multiplication");
print("4. Division");
print("5. Exit");
choice = int(input("Enter your choice: "));
if (choice>=1 and choice<=4):
print("Enter two numbers: ");
num1 = int(input());
num2 = int(input());
if choice == 1:
res = num1 + num2;
print("Result = ", res);
elif choice == 2:
res = num1 - num2;
print("Result = ", res);
elif choice == 3:
res = num1 * num2;
print("Result = ", res);
else:
res = num1 / num2;
print("Result = ", res);
elif choice == 5:
exit();
else:
print("Wrong input..!!");
Вот несколько примеров запуска вышеприведенной программы на Python, чтобы показать, как сделать простой калькулятор.
Это начальный вывод, дающий пользователям некоторое количество вариантов (5 вариантов), чтобы выбрать любой из этих 5 вариантов.
Теперь давайте сначала попробуем выполнить задачу сложения, выбрав или введя 1 в качестве ввода, а затем введите любые два числа, скажем 1 и 2, а затем нажмите клавишу ввода, чтобы проверить это:
Теперь давайте снова запустим программу калькулятора, чтобы проверить это время на вычитание двух чисел, скажем, 2 и 1, как показано в следующем примере:
Снова повторно запустите ту же программу, и на этот раз предоставьте 4 в качестве ввода для проверки задачи деления и введите два числа, то есть первое число как 20 и второе число как 3, затем нажмите клавишу ввода, как показано здесь в следующем примере выполнения:
Вот та же самая программа, написанная и работающая на оболочке Python. Это первый снимок:
Ниже приведен второй снимок:
Вот третий снимок:
Интересные записи:
1.4 Операторы присваивания
Как начать хранить очки игрока в игре? Или следить за здоровьем врага?
Для этого нам понадобятся операторы присваивания.
(оператор это символ вроде + или -.)
Они помогают сохранить значение в переменной для дальнейшего использования.
Код, приведённый внизу, присвоит переменной x значение 10, а затем выведет значение,
сохранённое в переменной x.
# Создать переменную x и сохранить в ней число 10.
x = 10
# Вывести число, сохранённое в x.
print(x)
# Это выводит букву x, но не значение x
print("x")
# Это выводит "x= 10"
print("x=",x)
Шаг |
Variables: x= Output: 10 x x= 10 |
Переменные пишутся вне кавычек.
Заметьте: Вышеприведённый пример также демонстрирует разницу между двумя вариантами:
x внутри кавычек и x снаружи кавычек.
Если x внутри кавычек,
то компьютер просто выводит x. Если x написан вне кавычек,
то компьютер выведет значение x.
Это бывает частой ошибкой у тех, кто учится программировать.
Video: The Assignment Operator
Присвоение не является тем же самым, что и алгебраическое уравнение. Не рассматривайте их
как одно и то же. В присвоении, слева от знака равенства находится переменная. Ничего другого
там быть не может.
Справа от знака равенства находится выражение. Выражением является всё то,
у чего в результате может быть значение.
Изучите код снизу. Он верен, даже несмотря на то, что он не является чистым
математическим уравнением. Математические уравнения устроены совсем по другому,
вопреки тому, что у них тоже есть перменные, числа и знак равенства.
Это выражение берёт текущее значение x, добавляет к нему единицу и сохраняет
результат обратно в x.
x = x + 1
Результатом нижеприведённого кода будет вывод цифры 6.
x=5 x = x + 1 print(x)
Следующее выражение является корректным, но бессмысленным. Компьютер
прибавит единицу к х, но результат никогда не будет сохранён или выведен.
x + 1
Нижеприведённый код выведет 5, а не 6, потому что программист забыл
сохранить результат $x + 1$ обратно в переменную x.
x=5 x + 1 print(x)
Выражение внизу не корректно, потому что слева от знака равенства находится
не только переменная.
x + 1 = x
У Python’а также есть операторы присвоения. Это позволяет программисту легче
изменять переменные. Например:
x += 1
Вышеприведённое выражение эквивалентно коду, приведённому ниже:
x = x + 1
Существуют операторы присвоения для сложения, вычитания, умножения и деления.
Знак равно
Основа калькулятора – это обработчик, который действительно выполняет кое-какую математику. Все операции (за исключением процентов) обрабатываются обработчиком знака равно, который вызывается нажатием на клавишу знака равно, Enter или другой операционной клавиши.
Обработчик equals берет current_op и добавляет его к значениям в стеке (2 значения, распакованные при помощи *self.stack) для получения результата. Результат отправляется обратно в стек в качестве единственного значения, и мы переходим к состоянию READY. Ошибки (исключения, например, деление на ноль) учитываются, и уведомление об ошибке может быть отображено при необходимости.
Python
def equals(self):
# Поддержка, позволяющая «=» повторять предыдущую операцию
# если новые данные небыли введены.
if self.state == READY and self.last_operation:
s, self.current_op = self.last_operation
self.stack.append(s)
if self.current_op:
self.last_operation = self.stack, self.current_op
try:
self.stack =
except Exception:
self.lcdNumber.display(‘Err’)
self.stack =
else:
self.current_op = None
self.state = READY
self.display()
|
1 |
defequals(self) # Поддержка, позволяющая «=» повторять предыдущую операцию # если новые данные небыли введены. ifself.state==READY andself.last_operation s,self.current_op=self.last_operation self.stack.append(s) ifself.current_op self.last_operation=self.stack-1,self.current_op try self.stack=self.current_op(*self.stack) exceptException self.lcdNumber.display(‘Err’) self.stack= else self.current_op=None self.state=READY self.display() |
Была также добавлена поддержка для повторяемых предыдущих операций при повторном нажатии знака равно. Это может быть реализовано при сохранении значения и оператора, когда задействуется знак равно. Повторное использование возможно при условии, что знак равно введен еще раз без выхода из режима READY (без пользовательского введения).
Текущая операция (current_op)
Переменная current_op содержит текущую активную операцию, которая будет задействована после того, как пользователь нажмет на кнопку уравнения. Если операция в данный момент прогрессирует, то мы сначала подсчитываем результат этой операции, выводим результат в стек и создаем новую.
Запуск новой операции также вводит в стек, таким образом, увеличивая его длину до 2, затем переключает режим на INPUT. Таким образом, мы получаем гарантию того, что любое вводимое далее число будет начинаться с нуля.
Python
def operation(self, op):
if self.current_op: # Завершение текущей операции
self.equals()
self.stack.append(0)
self.state = INPUT
self.current_op = op
|
1 |
defoperation(self,op) ifself.current_op# Завершение текущей операции self.equals() self.stack.append() self.state=INPUT self.current_op=op |
Обработчик операции для подсчета процентов работает немного иначе. Вместо этого, он управляет текущим содержимым стека напрямую. Вызов operation_pc берет последнее значение в стеке и делит его на 100.
Python
def operation_pc(self):
self.state = INPUT
self.stack *= 0.01
self.display()
|
1 |
defoperation_pc(self) self.state=INPUT self.stack-1*=0.01 self.display() |
Pathlib (Python 3.4+)
F-строки — это отличное решение, но некоторые строки, такие как пути файлов, имеют свои собственные библиотеки, которые заметно упрощают работу. Python 3 предоставляет pathlib в качестве удобной абстракции для работы с путями файлов.
Python
from pathlib import Path
root = Path(‘post_sub_folder’)
print(root)
# post_sub_folder
path = root / ‘happy_user’
# Делаем путь абсолютным
print(path.resolve())
# /home/weenkus/post_sub_folder/happy_user
|
1 |
frompathlib importPath root=Path(‘post_sub_folder’) print(root) # post_sub_folder path=root’happy_user’ # Делаем путь абсолютным print(path.resolve()) # /home/weenkus/post_sub_folder/happy_user |
1.2 Вывод
Нашим первым шагом к созданию калькулятора будет обучение выводу данных на экран.
Для того, чтобы это сделать, созданим простую программу. Эта программа просто выводит
надпись “Hello World.” на экран. На языке Python она выглядит вот так:
print ("Hello World.")
Video: The print function
Как же выглядит программа “Hello World”
на других языках программирования? У Википедии есть статья, показывающая варианты “Hello World”,
написаной на разных языках:http://en.wikipedia.org/wiki/Hello_world_program_examples
В зависимости от реализации “Hello World”, можно сделать начальные выводы о том, насколько
сложен каждый конкретный язык программирования. Интересно видеть, сколько в мире разных языков.
В общем, команда для вывода на экран в Python’e легко запоминается. Просто используйте
print.
После самой команды следуют скобки ( ). Внутри этих скобок находится то, что нужно
вывести на экран. Использовать скобки для передачи входных данных функции — обычное дело
как в математике, так и в программировании.
Люди, изучающие математику используют скобки, вычисляя выражения вроде
$sin(\theta)=cos(\frac{\pi}{2}-\theta)$. $sin$ и $cos$ — функции. Данные, переданные им,
находятся внутри скобок. В нашем случае разница лишь в том, что информация передаётся
в виде текста, а не в виде чисел.
Заметьте, что передаваемый функции текст заключён в кавычки.
Если текст находится в кавычках, компьютер выведет его точно таким,
каким он был подан. Например, следующая программа выведет 2+3:
print ("2+3")
У следующей программы кавычки вокруг $2+3$ отсутствуют, поэтому компьютер попытается
рассчитать результат, анализируя входные данные как математическое выражение. Он просто
выведет 5, а не 2+3.
print (2+3)
Попытка запустить программу с нижеприведённым кодом приведёт к ошибке:
компьютер постарается рассчитать “Hello World” как математическое выражение,
каковым оно вовсе не является.
print (Hello World)
Вышеуказанный код выдаст ошибку SyntaxError: invalid syntax, означающую,
что компьютер не знает, что значат “Hello” и “World”.
Print позволяет выводить много значений одновременно; нужно лишь перечислить их через запятые.
Например, следующий код выведет: Ответом на 10+10 является 20
print ("Ответом на 10+10 является",10+10)
Следующая строка кода выведет Ответом на 10+10 является 10+10.
Числа не складываются, потому что они наприсаны внутри кавычек. Всё, что написано
внутри кавычек, воспринимается компьютером как текст. Всё, что написано без кавычек,
компьютер воспринимает как математическое выражение либо «компьютерный код».
print ("Ответом на 10+10 является","10+10")
Должна ли запятая находиться внутри или снаружи кавычек?
Этот образец кода вовсе не будет работать. Потому, что в нём нет запятой, разделяющей
текст в кавычках и выражение 10+10. Вначале может показаться, что запятая поставлена,
однако можно заметить, что запятая находится внутри кавычек. Запятая, разделяющая аргументы,
поданные в функцию, должна находиться вне кавычек. Запятая, которую программист хочет
вывести на экран должна находиться внутри кавычек:
print ("Ответом на 10+10 является," 10+10)
Следующий пример будет работать потому, что после текста следует запятая, отделяющая
print ("Ответом на 10+10 является,", 10+10)