Что такое корреляция

Критерии и методы

КРИТЕРИЙ СПИРМЕНА

Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Чарльз Эдвард Спирмен

1. История разработки коэффициента ранговой корреляции

Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.

2. Для чего используется коэффициент Спирмена?

Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.

1. Коэффициент корреляции Спирмена обладает следующими свойствами:
2. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
3. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
4. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
5. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

3. В каких случаях можно использовать коэффициент Спирмена?

В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.

Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).

Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.

4. Как рассчитать коэффициент Спирмена?

Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1. Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
2. Определить разности рангов каждой пары сопоставляемых значений (d).
3. Возвести в квадрат каждую разность и суммировать полученные результаты.
4. Вычислить коэффициент корреляции рангов по формуле:

Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:

5. Как интерпретировать значение коэффициента Спирмена?

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.

Также для оценки тесноты связи может использоваться шкала Чеддока:

_xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая

Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.

Понятие корреляции

Определение 1

Корреляция – это статистическая зависимость двух и более величин, которые выбираются случайным образом.

В переводе с латинского, корреляция дословно обозначает связь, соотношение. Если в этой зависимости происходит изменение одной из величин, то это ведет к изменению других, связанных с нею величин. Для определения степени взаимосвязи величин используется математический инструмент – коэффициент корреляции. Обычно он обозначается латинской буквой R. Корреляционная связь возникает только тогда, когда осуществляется закономерное изменение другой величины. Если этого не происходит, но имеется изменение какой-либо другой статистической характеристики, то связь между величинами будет называться статистической, но не корреляционной.

Замечание 1

Примечательно, что термин «корреляция» был введён палеонтологом, который установил связь между различными органами доисторических животных с целью восстановления их образа. В математике и статистике этот термин стал использоваться в конце 19-го века благодаря Фрэнсису Гальтону.

Корреляционная связь не всегда имеет причинно-следственный характер. Коэффициент устанавливает лишь взаимосвязь со статистической точки зрения. Однако, наличие корреляции может говорить о том, что у двух случайных величин может быть схожая первопричина. Если корреляции между двумя величинами нет, то это не означает полного отсутствия связей между ними. В случае сложной связи, установленной между объектами, корреляция неспособна ее выявить.

Литература

• Гмурман В. Е.ru_uk. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
• Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.
• Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
• Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А. А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8.

Порядок вычисления

1. Находят усредненные
   данные для обоих рядов (x и y),
   т.е. средние

величины по формуле
(для коэффициентов определяют общие
коэффициенты):

М
=

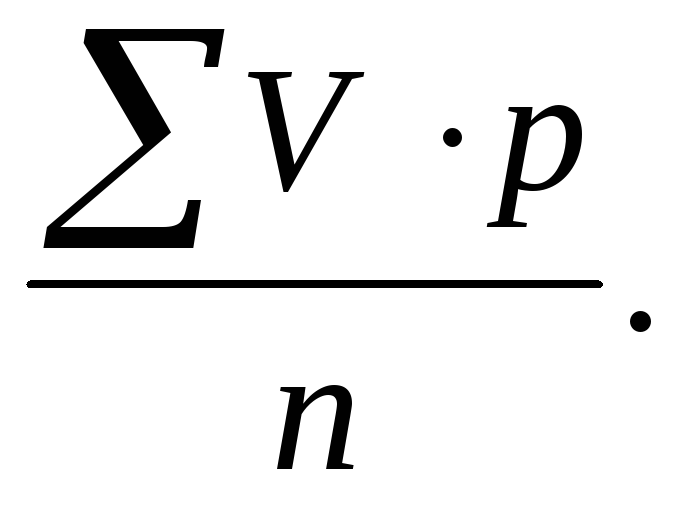
2. Определяют
отклонения от этих усредненных величин
(d_x
= M_x
– x,

d_y
= M_y
-y)
с обозначением соответствующего
отрицательного знака. В данном случае:
d_x=
25 — 15 =10;d_x=
25 -20 =5 и т.д. Для ряда y
: d_y=18,4
– 22,0 = — 3,6;d_y=18,4 – 28 = —
9,6 и т.д.

3. Возводят
полученные результаты в квадрат и
получают суммы этих квадратов

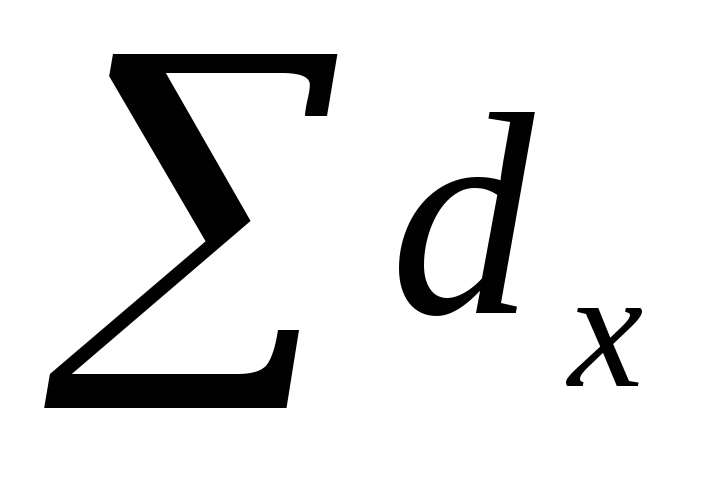(иd_y).

4. Находят
произведения каждого d_x
на d_y
и получают их сумму ().

5. Подставляют
полученные данные в формулу:

r_xy
=

При определении
коэффициента линейной корреляции
Пирсона на программируемых калькуляторах
надо иметь два основных документа:
специальную программу вычисления и
инструкцию по ее применению. Для
персональных компьютеров разработаны
также специальные программы вычисления
на языке Бейсик.

Так как полученные
коэффициенты определяются, как правило,
на материалах выборочного исследования,
то всегда необходимо убеждаться в
степени их надежности. Представительность
(репрезентативность) коэффициента
линейности корреляции также может
определяться по специальным таблицам
(приложение 2) или ориентировочно – по
средним ошибкам, которые должны для
обоснования значимости связи быть в 3
раза меньше своего коэффициента
корреляции. Коэффициент считается
представительным, если полученная
величина его превышает критическое
значение при p<
0,05 и заданном числе степеней свободы
n,
которое равняется n – 2. Полученная в
задаче величина 0,86 превышает критический
уровень 0,75 при n
= 5 и p<
0,05.

При отсутствии
таблицы критических значений коэффициентов
корреляции представительность
коэффициента может быть определена по
величине средней ошибки m
(при числе парных наблюдений менее 100):

m_r=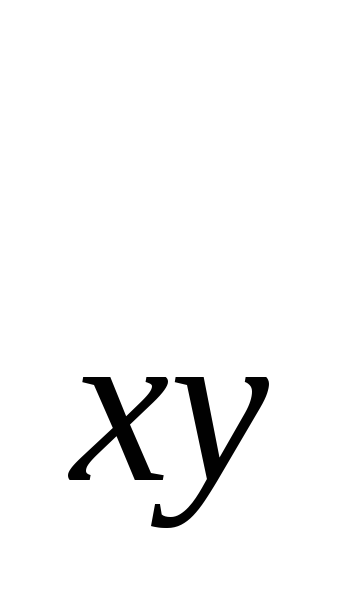

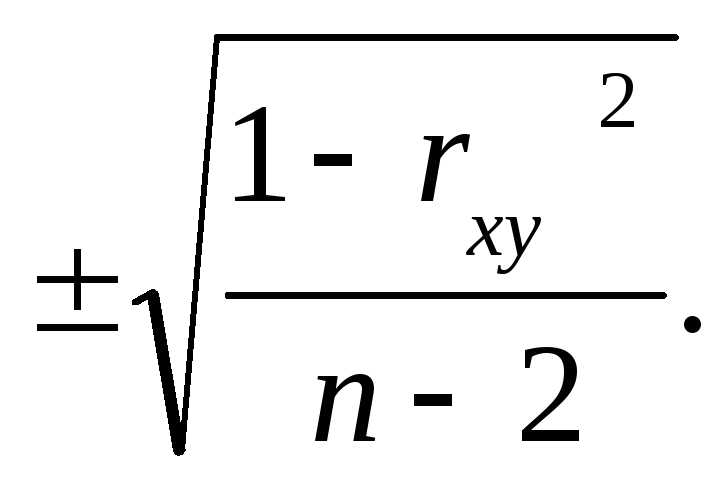
Можно
для определения средней ошибки
использовать и более упрощенную формулу:

m_r=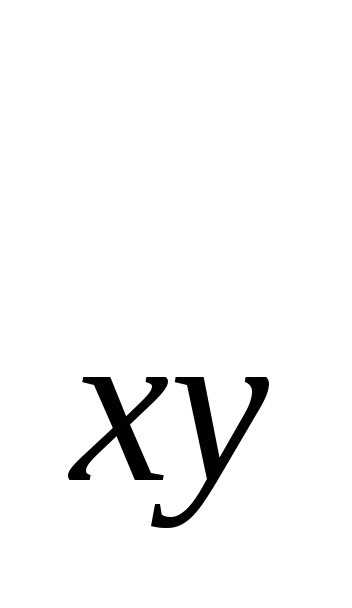

Коэффициент
корреляции будет достоверен лишь в том
случае, когда он превышает свою ошибку
в 3 – 4 раза. Оценку значимости проводят
и по t-
критерию, его величину определяют по
формуле:

t
=r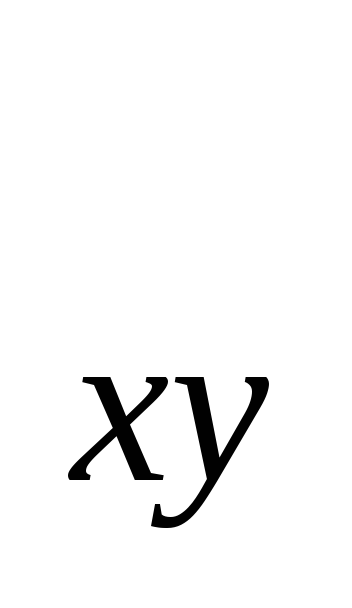
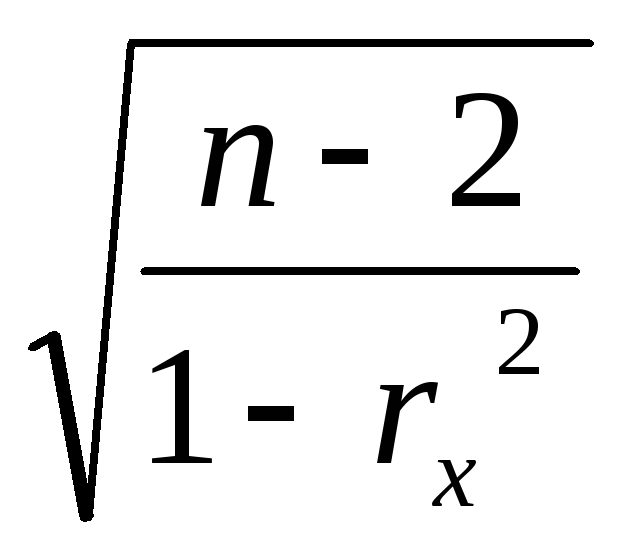
при n<100.

Для нашей задачи:

t
= 0,86

Так как t
> 2, то это говорит о достаточной
достоверности влияния прививок на
уровень заболеваемости и о значимости
полученных результатов. Оценку критерия
t
можно давать и по специальным оценочным
таблицам, в Соответствии с которыми при
уровне значимости p
, равном 0,05 (5%), и числе степеней свободы
4 и 5 этот критерий должен равняться
соответственно 2,776 или 2,571. В данном
случае доверительный критерий t
больше указанных табличных значений,
следовательно, получены хорошие
результаты. Достоверность корреляции
доказана, нулевая гипотеза предусматривает
отсутствие корреляционной связи. Если
полученный коэффициент корреляции не
удовлетворяет принятому уровню
значимости, т.е. его вероятность ниже
0,95, то это является основанием для
признания нулевой гипотезы правильной.

Правильная трактовка
коэффициентов корреляции предполагает
нормальное распределение сопряженных
величин коррелируемых рядов x
и y.
Однако при малом числе наблюдений и
сравнительно сильной корреляции
вычисленный коэффициент корреляции не
всегда будет точной оценкой для
генеральной совокупности. В этих случаях
коэффициент r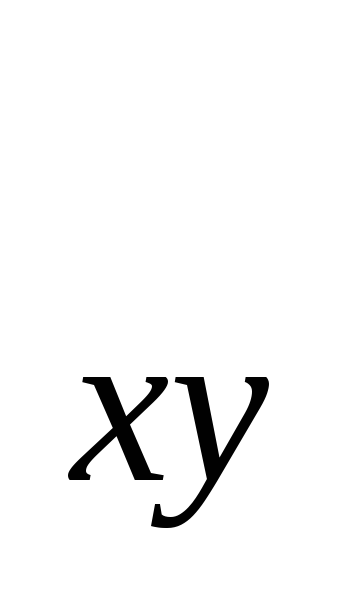
целесообразно заменить преобразованной
величиной Z
(преобразование Фишера).

Форма распределения
величины Z
почти не отличается от формы нормального
распределения, так как мало зависит от
численности выборки и значения r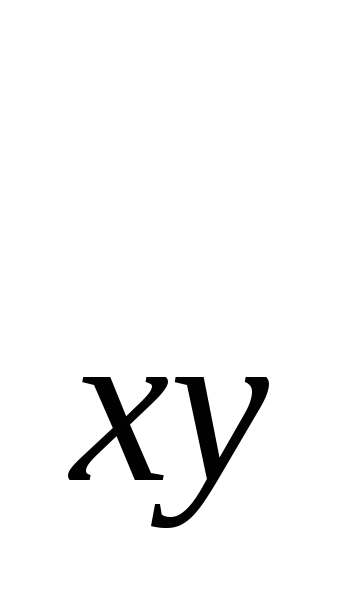
в генеральной совокупности. Только с
помощью величины Z
можно определить достоверность различий
между двумя коэффициентами корреляции,
а также объединить данные по нескольким
корреляциям. Преобразование r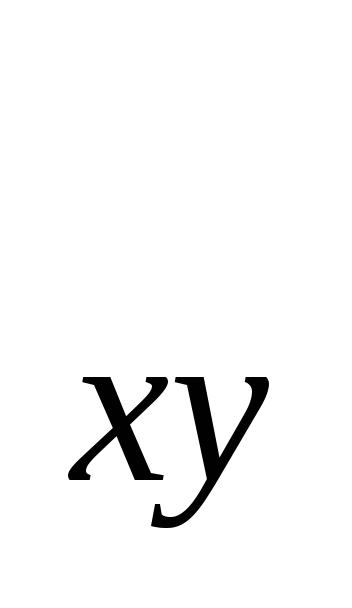
в Z
проводится по специальным таблицам,
имеющимся в различных пособиях по
статистике.

В заключение
следует обратить внимание на возможность
пользования следующих наиболее доступных
и простых формул определения средних
ошибок коэффициентов корреляции

1. Ошибка коэффициента
   корреляции, вычисленного по методу
   Спирмена:

m=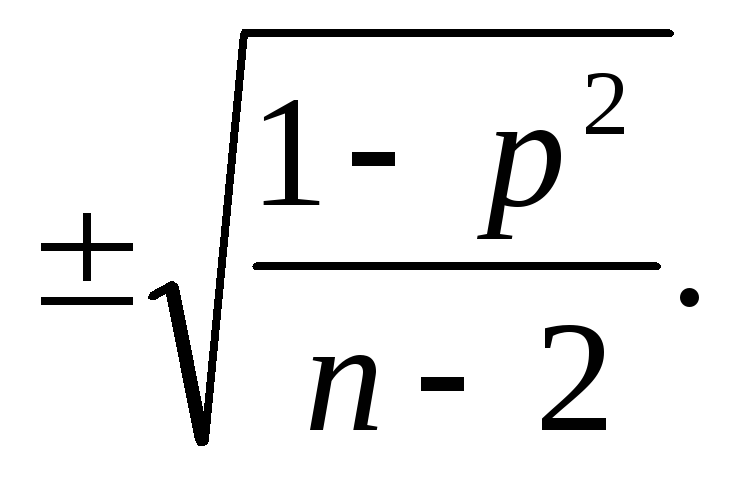

1. Ошибка коэффициента
   корреляции, вычисленного обычным
   методом Пирсона:

m_r=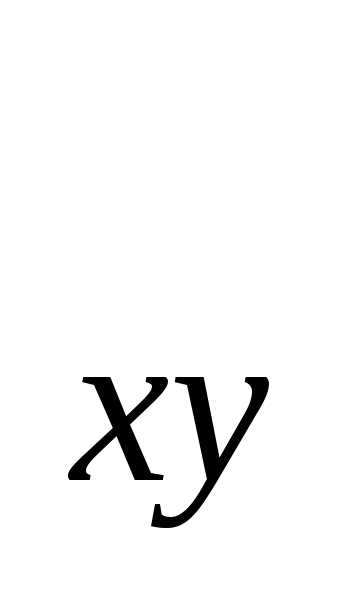

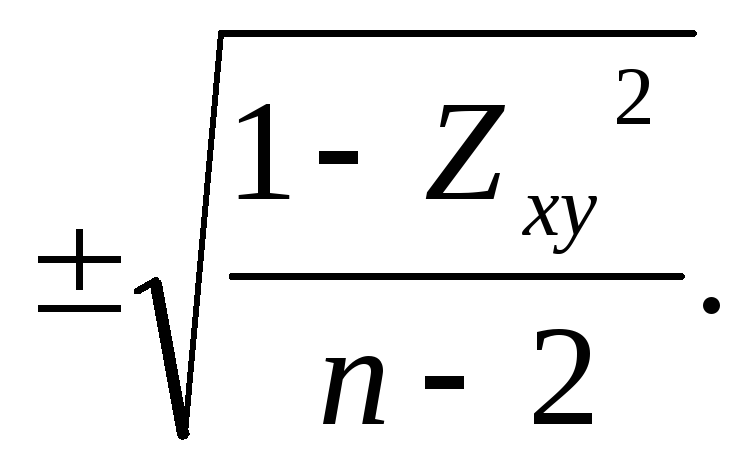
Корреляция и диверсификация

Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации инвестиционных активов в портфеле. Корреляция и диверсификация неразрывно связаны, что понятно даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.

Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:

Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:

Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.

А вот пример портфеля двух активов с корреляцией близкой к 0:

Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:

Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.

Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:

Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:

Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Использование ПО при проведении корреляционного анализа

Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный анализ в Excel предполагает вычисление следующих парамет­ров с использованием функций:

1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ (массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.

Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию ПИРСОН (PEARSON) с теми же массивами.

Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».

После указания исходных данных получаем график.

2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).

3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.

9.1.5. Стандартизованный регрессионный коэффициент. Значимость

Если в задаче простой линейной регрессии стандартизовать зависимую и независимую переменные, т.е. преобразовать переменные так, чтобы их дисперсии стали равными единице, то регрессионный коэффициент a совпадет с коэффициентом корреляции, а свободный член будет равен нулю, что видно непосредственно из вышеприведенных формул. Статистическая оценка значимости не меняется при допустимом преобразовании шкал, описывающих переменные, поэтому мы будем вести речь о значимости для стандартизованных переменных, поскольку это наиболее удобно.

Во-первых, заметим, что оценка ​\( R^2 \)​ не меняется при стандартизации, как и при любом другом линейном преобразовании переменных, поскольку на одинаковые константы умножаются все суммы квадратов ​\( S_{total} \)​, \( S_{model} \) и \( S_{error} \). Для оценки значимости аналогично тому, как это делали в дисперсионном анализе, составляется F-отношение:

\[ F=\frac{S_{model}/df_{model}}{S_{error}/df_{error}} \]

Чем больше это отношение, тем больше у нас оснований склониться к тому, что наша модель надежна, и тем уже доверительный интервал вокруг полученного углового коэффициента . Для числителя число степеней свободы равно единице, а для знаменателя n – 2, где n объем выборки (подробнее о степенях свободы в следующем параграфе). Далее — знакомая уже процедура: по полученному значению F находится вес верхнего хвоста соответствующего распределения Фишера, который отсекается данным значением.

Разумеется, значимость регрессионного коэффициента в простой линейной регрессии совпадет со значимостью коэффициента корреляции.

Что представляет собой корреляция?

Термин «корреляция» пугает многих людей и кажется чем-то сложным и непонятным. Однако на практике ничего устрашающего в ней нет. Корреляция – это всего лишь показатель, показывающий зависимость между событиями или объектами.

Данное понятие применяется в экономическом и статистическом анализе, психологии, биологии, математике. Например, если посмотреть на небо и увидеть густые и темные тучи, то можно прийти к выводу, что скоро пойдет дождь. Однако наше умозаключение не дает 100% гарантии. Это и является отличительной особенностью корреляцию от линейной зависимости.

Что такое корреляция?

Корреляция – это взаимозависимость случайных факторов. Она отображает приближенную взаимосвязь и не дает точных ответов. Например, в стране выросла безработица и увеличилось количество преступлений. Можно предположить, что на второй фактор повлияли первый. Но на уровень преступности также влияют воспитание, менталитет людей, уровень образования. Составить точный прогноз нереально, так как всегда есть дополнительные факторы.

Связь может быть трех видов:

• сильной;
• слабой;
• отсутствовать.

Например, повышения уровня радиации негативно сказывается на здоровье человека. Межу событиями имеется обратно пропорциональная зависимость – увеличения радиации приводит к ухудшению здоровья. Коэффициент корреляции при этом имеет отрицательное значение.

Некоторые события или явления практически никак не связаны друг с другом. Утром у вас разрядился телефон, а вчера в маршрутке вам на ногу наступил мужчина. Ни одно из событий не влияет на другое. В данном случае коэффициент корреляции равен нулю.

Если коэффициент больше нуля и стремится к 1, то такая корреляция называется положительной. Она показывает прямую взаимосвязь между событиями. Например, чем выше уровень знаний, тем выше шансы поступить в университет на бюджет.

Корреляция цены на нефть и курса доллара

Цена на нефть и курс американского доллара имеют обратную корреляционную связь. При росте стоимости «черного золота» курс доллара снижается и наоборот.

США обладают самой мощной промышленностью в мире и на ее нужды требуется просто огромное количество нефти.  В то же время Штаты входят в первую десятку стран по уровню добычи этого природного ресурса. При этом США значительную часть добытой нефти экспортируют, что вызывает дефицит в промышленности. Для его покрытия американцы ежегодно импортируют свыше 8 миллиардов баррелей нефти.

Данного объема достаточно для влияния на курс национальной валюты. Увеличение спроса США на нефть приводит к увеличению цены на международном рынке. В свою очередь, рост объемов импорта влияет на стоимость произведенных товаров. В итоге на валютном рынке наблюдается избыток американской валюты, и ее курс начинает падать.

Корреляция в управлении инвестиционными активами

Корреляция активно используется инвесторами при формировании и управлении своих инвестиционных портфелях. Логично, что нельзя держать все свои активы в одном месте. Диверсификация позволяет значительно снизить риски.

Например, инвестор покупает акции одной крупной компании и нескольких мелких. Коэффициент корреляции акций гигантов отрасли и небольших предприятий приблизительно равен +0,8. Это достаточно большое значение и оно характеризует прямую зависимость между объектами. При падении акции крупной компании существует большая вероятность, что стоимость ценных бумаг небольших фирм тоже снизится существенная. В данном случае лучше подбирать активы таким образом, что корреляционные связи были минимальными.

Для этого, например, инвестор может составить свой портфель из акций и облигаций или акций и казначейских векселей. Облигации между собой, как и акции, также имеют прямую связь. Их коэффициент еще выше. Однако между облигациями и акциями такой зависимости нет, что и позволяет инвестору снизить риски.

Также наблюдается зависимость между странами и даже регионами. Чем ближе они находятся, тем выше коэффициент корреляции. Например, для Канады и США он составляет 0,9. В то же время для Японии и США он на 4 десятых меньше. Собственно, инвестору более выгодно покупать активы эмитентов из разных регионов.

Золото и ценные бумаги практически не коррелируются. Однако серебро и золото очень зависимы друг от друга, так же, как и евро и американский доллар. Их использование в рамках одного инвестиционного портфеля нецелесообразно.

Корреляция – это удобный и необходимый инструмент в различных сферах жизни. Она не является панацеей, но позволяет достаточно точно установить причинно-следственные связи между явлениями.

Взаимосвязь явлений в природе и обществе

Впервые термин «корреляция» был использован в палеонтологии – изучении ископаемых животных. Находя похожие части скелетов динозавров, ученые могли обосновать принадлежность их к одному виду. Схожие биологические останки в горных породах в Азии и Африке позволили сделать вывод о формировании этих слоев в один геологический период.

Например, есть убеждение, что полные люди добры и великодушны. Современная психология не может найти прямой логической связи темперамента и физиологии. Можно сделать два предположения:

• человек с философским и гуманным складом ума находит удовольствие в еде, а не в том, чтобы пакостить окружающим;
• человек с хорошим аппетитом сосредоточен на питании, а не на том, чтобы строить козни.

Статистик не ставит себе задачу: выяснить, какое из предположений правильное? Он лишь постарается проверить, верное ли утверждение в принципе. Позднее, возможно, физиолог изучит функции печени и сделает вывод о ее влиянии на гормональный фон и образование жиров в организме. Гормоны ответят за хорошее настроение, а отложение жиров – за внешний облик. Причина же будет лежать в области генетики.

Графическое представление коэффициента Фехнера

Пример №1. При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).

X1	9	9	11	9	8	11	10	8	10
X2	10	11	10	12	11	12	12	10	9

Пример №2.
Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:

,

где n_a — число совпадений знаков отклонений индивидуальных величин от средней; n_b — число несовпадений.

Коэффициент Фехнера может принимать значения от -1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф =-1 свидетельствует о возможном наличии обратной связи.

Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:

Xi	Yi	Знаки отклонений значений признака от средней	Совпадение (а) или несовпадение (в) знаков
Для Xi	Для Yi
8	40	—	—	А
9	50	—	+	В
10	48	—	+	В
10	52	—	+	В
11	41	+	—	В
13	30	+	—	В
15	35	+	—	В

Для примера: .

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Пример №2
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
Средние значения:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
12	220	+	—	B
9	1070	—	+	B
8	1000	—	+	B
14	606	+	—	B
15	780	+	+	A
10	790	—	+	B
10	900	—	+	B
15	544	+	—	B
93	5910

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Интервальная оценка для коэффициента корреляции знаков

Пример №3.
Рассмотрим на примере расчет коэффициента корреляции знаков по данным, приведенным в таблице:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
96	220	+	—	B
52	1070	—	+	B
60	1000	—	+	B
89	606	+	—	B
82	780	+	+	A
77	790	—	+	B
70	900	—	+	B
92	544	+	—	B
618	5910

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Оценка коэффициента корреляции знаков. Значимость коэффициента корреляции знаков.
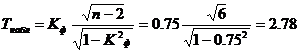По таблице Стьюдента находим t_табл:
t_табл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент корреляции знаков статистически — значим.

Доверительный интервал для коэффициента корреляции знаков.
Доверительный интервал для коэффициента корреляции знаков.
r(-1;-0.4495)

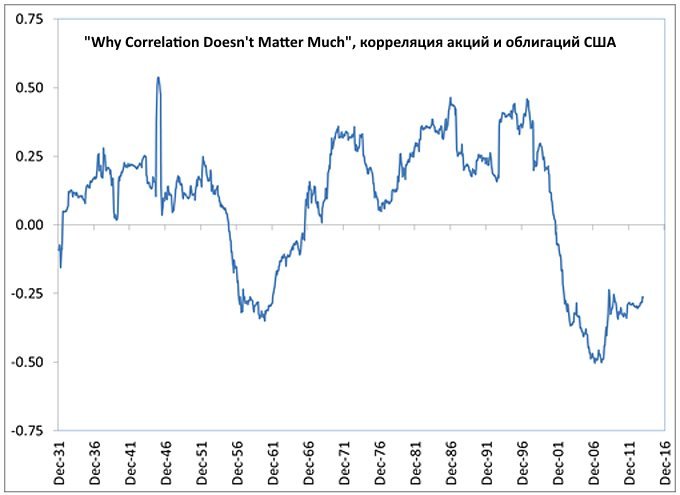
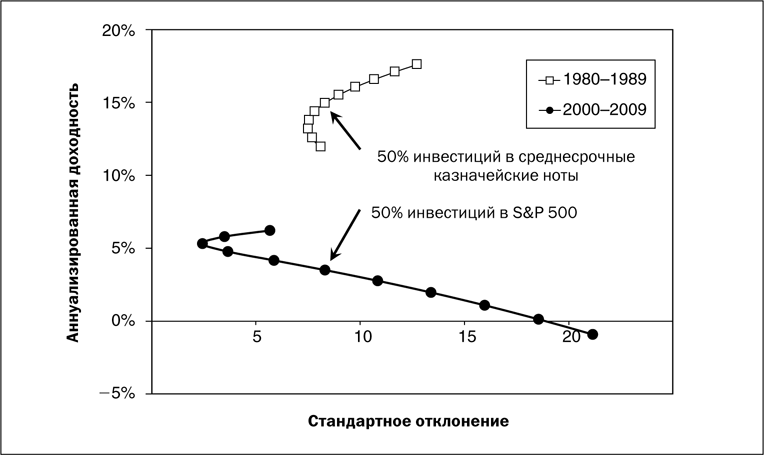
Зависимость корреляции от времени

Как уже упоминалось выше, корреляция не является константой и сама меняется в зависимости от времени. К примеру, корреляция между акциями США и пятилетними гос. облигациями с 1926 по 2013 годы была равна 0.07 — т.е. зависимость почти не прослеживалась. Однако на истории корреляция колебалась от -0,5 до +0,5, причем в XX веке после Великой Депрессии она находилась в отрицательной зоне лишь с середины 50-х по середину 60-х годов. В период с 1970-1985 корреляция акций и облигаций была равна 0.3%, тогда как с 2002-2013 обратной по знаку:

Таким образом, задача поиска доходности зависит от двух неизвестных: корреляции и доходности активов на рассматриваемом промежутке, причем эта доходность достигается с различным риском (отклонением от среднего значения). Отрицательная корреляция в общем случае позволяет достигать большей доходности с меньшим риском по сравнению с менее доходным активом:

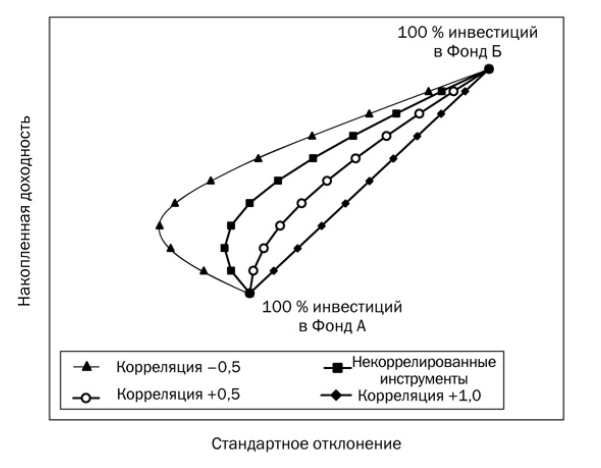
Фонд А — менее волатильный и менее доходный актив (облигации), фонд Б — более волатильный и доходный (акции). Стандартное отклонение определяет размах колебаний относительно среднего значения актива. Такое соотношение, как на рисунке выше, наблюдается на длинной истории — однако в пределах десятилетий может довольно сильно меняться:

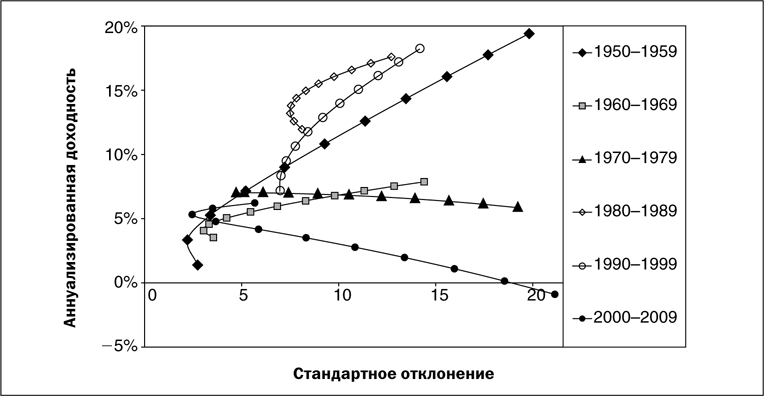
Видно, что на протяжении 2000-2009 годов американские акции даже ушли в минус, в результате чего кривая получила движение вниз, а не вверх. Следовательно, корреляция ничего не говорит об абсолютной доходности — первая может мало меняться на протяжении 20 лет, однако результаты одинаковых портфелей на следующих друг за другом 10-летних промежутках разойдутся.

Так, в кризисные 70-е и растущие 80-е корреляция американских акций и 5-летних облигаций была в среднем одинакова (около 0.25), однако доходность портфеля 50 на 50 во втором случае была 15% годовых, а в первом лишь около 7%. Ниже отдельно показаны наилучшее и наихудшее американское десятилетие с 1950 года:

Разбираемся с терминологией и классификацией

Если не привязываться к трейдингу, то под устойчивой корреляцией понимается статистическая связь между двумя или более случайными величинами. Если одна из них меняется, то соответствующая реакция появляется и на другой. Простейший пример – связь нефти и сырьевых валют, падение стоимости «черного золота» сказывается на их котировках.

Классификацию можно привести по нескольким критериям. Если в качестве основы взять устойчивость связи, то выделяются:

• Устойчивая корреляция. Сохраняется в течение длительного промежутка времени, обусловлена фундаментальными факторами. Пример такой взаимосвязи – стоимость газа и нефти. Цена голубого топлива запаздывает на 9 месяцев по сравнению с «черным золотом», это особенности ее расчета. Еще один пример – стоимость золота и состояние мировой экономики. С ростом неуверенности в темпах роста инвесторы переводят деньги в защитные активы, желтый металл входит в их число. Его цена в периоды кризисов всегда растет.
• Неустойчивая или случайная. На отдельных участках истории может формироваться высокая прямая или обратная корреляция между не связанными инструментами. Спрогнозировать, как быстро она разрушится, невозможно. Например, между стоимостью акций Apple и CFD на сахар может формироваться кратковременная корреляция, но использовать ее в торговле невозможно.

По направлению связи выделяют:

• Прямую корреляцию. Увеличение одной величины статистически приводит к росту других.
• Обратная взаимосвязь. Рост одной величины становится причиной падения другой. Простейший пример – при удорожании нефти пары USDRUB, EURRUB также идут вверх из-за снижения российской валюты.

Возможна классификация и по «силе» связи:

• ±1,0 – 100% корреляция, в природе не встречается.
• 0,7…1,0 и -0,7…-1,0 – сильная связь, может использоваться в торговле.
• 0,3…0,7 и -0,3…-0,7 – корреляция средней силы.
• 0…±0,3 – в торговле не учитывается, между инструментами нет статистически значимой связи.

Значение слова Корреляция по словарю Брокгауза и Ефрона:

Корреляция (лат. correlatio) — термин, предложенный покойным профессором казанского университета Н. В. Крушевским (см.) для обозначения таких звуковых чередований (в области одного и того же языка), которые не обусловливаются более, в данный момент жизни языка, никакими реальными причинами и представляют собой просто остаток или след некогда действовавшего звукового процесса. Члены такого чередования (коррелятивы) уже утратили известную необходимую связь, соединявшую их между собой, и находятся в отношении простого «сосуществования» или «соотношения». Так, напр., гласные о и у в словах муха и мошка в настоящее время суть коррелятивы, так как их чередование теперь ничем не обусловлено. Таково же взаимное отношение звуков е, о, е в формах: реку, про-рок, речь и т. д. См. также Дивергенция (см.). Ср. Крушевский, «К вопросу о гуне» («Р. Филол. Вест.», 1887, кн. I, и отдельно: Введение). его же, «Ueber die Lautabwechslung» (Казань, 1881). его же, «Очерк науки о языке» (Казань, 1883). Бодуэн де-Куртенэ, «Некоторые отделы сравн. грамматики слав. яз.» («Р. Филол. Вест.», 1881, кн. 2). его же, «Pr &oacute. ba teorji alternacyj fonetyczuych» (Краков, 1894, ч. I). С. Б — ч.