Как в excel построить кривую нормального распределения

Содержание:

Свойства
Примеры задач с использованием понятия функции распределения
3.2.1. Эмпирическая функция распределения. Кумулята
Нормальное распределение: теоретические основы
Нормальное распределение в статистике
Построение гистограмм распределения в Excel
На какие вопросы отвечает гистограмма распределения?
Значение
Распределения
Нормальное распределение в статистике

Свойства

Моменты

Моментами и абсолютными моментами случайной величины X называются математические ожидания X p и |X|p{\displaystyle \left|X\right|^{p}}, соответственно. Если математическое ожидание случайной величины μ = 0, то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых p.

Если X имеет нормальное распределение, то для неё существуют (конечные) моменты при всех p с действительной частью больше −1. Для неотрицательных целых p, центральные моменты таковы:

EXp={p=2n+1,σp(p−1)!!p=2n.{\displaystyle \mathrm {E} \left={\begin{cases}0&p=2n+1,\\\sigma ^{p}\,\left(p-1\right)!!&p=2n.\end{cases}}}

Здесь n — натуральное число, а запись (p − 1)!! означает двойной факториал числа p − 1, то есть (поскольку p − 1 в данном случае нечётно) произведение всех нечётных чисел от 1 до p − 1.

Центральные абсолютные моменты для неотрицательных целых p таковы:

E⁡|X|p=σp(p−1)!!⋅{2πp=2n+1,1p=2n.}=σp⋅2p2Γ(p+12)π.{\displaystyle \operatorname {E} \left=\sigma ^{p}\,\left(p-1\right)!!\cdot \left.{\begin{cases}{\sqrt {\frac {2}{\pi }}}&p=2n+1,\\1&p=2n.\end{cases}}\right\}=\sigma ^{p}\cdot {\frac {2^{\frac {p}{2}}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.}

Последняя формула справедлива также для произвольных p > −1.

Бесконечная делимость

Нормальное распределение является бесконечно делимым.

Если случайные величины X1{\displaystyle X_{1}} и X2{\displaystyle X_{2}} независимы и имеют нормальное распределение с математическими ожиданиями μ1{\displaystyle \mu _{1}} и μ2{\displaystyle \mu _{2}} и дисперсиями σ12{\displaystyle \sigma _{1}^{2}} и σ22{\displaystyle \sigma _{2}^{2}} соответственно, то X1+X2{\displaystyle X_{1}+X_{2}} также имеет нормальное распределение с математическим ожиданием μ1+μ2{\displaystyle \mu _{1}+\mu _{2}} и дисперсией σ12+σ22.{\displaystyle \sigma _{1}^{2}+\sigma _{2}^{2}.}
Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.

Максимальная энтропия

Нормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину.

Примеры задач с использованием понятия функции распределения

Случайные числа в excel

Пример 1

Приведен ряд распределений появления события $A$ в трех опытах

Рисунок 8.

Найти функцию распределения вероятностей и построить её график.

Решение.

При $x\le 1$, $F\left(x\right)=0$;

При $1

При $2

При $x>3$, $F\left(x\right)=0,2+0,1+0,3+0,4=1$;

Отсюда получаем следующую функцию распределения вероятностей:

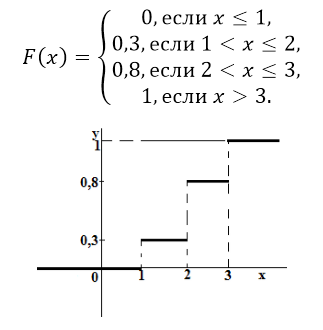Рисунок 9.

Пример 2

Случайная величина задана следующей функцией распределения:

Рисунок 10.

Найти вероятность, что величина $X$ будет принадлежать интервалу $\left(\frac{7}{6};;1,2\right)$.

Решение. Нам необходимо найти значение $P\left(\frac{7}{6}
\[P\left(\frac{7}{6}\le XОтвет: 0,1.

3.2.1. Эмпирическая функция распределения. Кумулята

Дисперсия и стандартное отклонение в excel

Эмпирическая
функция распределения. Каждая
генеральная совокупность имеет некоторую
функцию распределения
F(x).
Обычно она неизвестна. По выборке можно
найти эмпирическую функцию распределения
F*(x).

Эмпирической
функцией распределенияF*(x)
(функцию
распределения выборки) называют функцию
F*(x),
которая определяет для каждого значения
x
относительную частоту события X<x.

Теоретической
функцией распределения называют функцию
распределения генеральной совокупности,
которая определяет вероятность события
X<x.
На основании закона больших чисел (в
форме Бернулли) эмпирическая функция
распределения выборки F*(x)
служит для приближенного представления
теоретической функции распределения
генеральной совокупности. Итак,

, (3.3)

где
n
— объем выборки,
—
число всех элементов выборки, значения
которых строго меньше x.
Отличие эмпирической функции распределения
F*(x)
от реальной (теоретической) F(x)
заключается в том, что для ее составления
берется не вся генеральная совокупность,
а выборка, и вероятность p_i
заменяется относительной частотой
.
Т.о., теоретическая функцияF(x)
определяет вероятность
события X<x,
аэмпирическая
функция F*(x)
определяет относительную
частоту
этого же события.

Следует
заметить, что вероятность p_i
— тоже
относительная частота, только примененная
к самой генеральной совокупности: p_i=
N_iN.
Отсюда возникают два важных свойства
эмпирической функции распределения
F*(x):

(3.4)

т.е.
эмпирическая функция распределения в
каждой своей точке сходится по вероятности
к соответствующей ей теоретической
функции распределения. Т.о., для всякой
эмпирической функции распределения
существует равная ей теоретическая
функция распределения некоей генеральной
совокупности. Следовательно, эмпирическая
функция распределения обладает всеми
свойствами теоретической функции
распределения ДСВ (см. гл. II):

F*(x);
F*(x)
– неубывающая функция;
если
задана ранжированная последовательность
вариант x₁,
x₂,…,x_n,
то F*(x₁)=0,
F*(x_n+0)=1.

Итак,
если выборка задана вариационным рядом
(x_i,
),
то эмпирическая функция распределения
имеет вид:

(3.5)

График
эмпирической функции распределения
называют кумулятой.
Для выборки, взятой из генеральной
совокупности, имеющей вид ДСВ, кумулята
носит характер ступенчатой ломаной
(Рис. 1). Для выборки, взятой из генеральной
совокупности, имеющей вид НСВ, для
построения кумуляты точки с координатами
(x_i;
F*(x_i))
соединяют отрезками. В таком случае
кумулята носит характер непрерывной
ломаной.

Задача
1. Контролер
ОТК анализировал отклонение длины
деталей в мм от Госстандарта на основе
выборки, состоящей из 50 деталей. По
результатам выборки построить эмпирическую
функцию распределения:

x_i	-2	1	3	5	8
n_i	8	5	11	16	4	6

Решение:

Объем
выборки равен n=8+5+11+16+4+6=50.
Тогда вариационный ряд относительных
частот имеет вид:

x_i	-2	1	3	5	8
n_in	0.16	0.10	0.22	0.32	0.08	0.12

В соответствии с
формулой (1.5) построим эмпирическую
функцию распределения:

Рис.
1

Если
задан интервальный вариационный ряд,
то для составления эмпирической функции
находят середины интервалов x_i+h/2
и по ним получают эмпирическую функцию
аналогично точечному вариационному
ряду. Т.о., вся часть выборки, попавшая
в интервал (х_i, x_i+h],
как бы “концентрируется” в середине
этого интервала – в точке x_i+h/2.

Нормальное распределение: теоретические основы

Гистограмма в excel

Примерами случайных величин, распределённых по нормальному закону, являются рост человека,
масса вылавливаемой рыбы одного вида. Нормальность распределения означает следующее: существуют значения
роста человека, массы рыбы одного вида, которые на интуитивном уровне воспринимаются как «нормальные»
(а по сути — усреднённые), и они-то в достаточно большой выборке встречаются гораздо чаще, чем
отличающиеся в бОльшую или меньшую сторону.

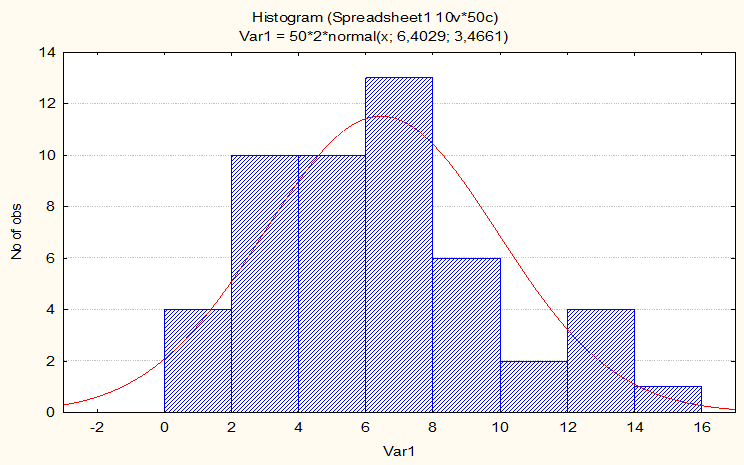
Нормальное распределение вероятностей непрерывной случайной величины (иногда —
распределение Гаусса) можно назвать колоколообразным из-за того, что симметричная относительно среднего
функция плотности этого распределения очень похожа на разрез колокола (красная кривая на рисунке выше).

Вероятность встретить в выборке те или иные значение равна
площади фигуры под кривой и в случае нормального распределения мы видим, что под верхом «колокола»,
которому соответствуют значения, стремящиеся к среднему, площадь, а значит, вероятность, больше, чем под
краями. Таким образом, получаем то же, что уже сказано: вероятность встретить человека «нормального» роста,
поймать рыбу «нормальной» массы выше, чем для значений, отличающихся в бОльшую или меньшую сторону.
В очень многих случаях практики ошибки измерения распределяются по закону, близкому к нормальному.

Остановимся ещё раз на рисунке в начале урока, на котором представлена функция плотности нормального распределения.
График этой функции получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. На ней
столбцы гистограммы представляют собой интервалы значений выборки, распределение которых близко (или, как принято говорить в
статистике, незначимо отличаются от) к собственно графику функции плотности нормального распределения, который
представляет собой кривую красного цвета. На графике видно, что эта кривая действительно колоколообразная.

Нормальное распределение во многом ценно благодаря тому, что зная только математическое
ожидание непрерывной случайной величины и стандартное отклонение, можно вычислить любую вероятность, связанную
с этой величиной.

Нормальное распределение имеет ещё и то преимущество, что один из наиболее простых
в использовании статистических критериев, используемых для проверки статистических гипотез — критерий
Стьюдента — может быть использован только в том случае, когда данные выборки подчиняются нормальному
закону распределения.

Функцию плотности нормального распределения непрерывной случайной величины
можно найти по формуле:

где x — значение изменяющейся величины, —
среднее значение, —
стандартное отклонение, e=2,71828… — основание натурального логарифма, =3,1416…

Свойства функции плотности нормального распределения

для всех значений аргумента функция плотности положительна;
если аргумент стремится к бесконечности, то функция плотности стреится к нулю;
функция плотности симметрична относительно среднего значения: ;
наибольшее значение функции плотности — у среднего значения: ;
кривая функции плотности выпукла в интервале и вогнута на остальной части;
мода и медиана нормального распределения совпадает со средним значением;
при нормальном распределении коэффициенты ассиметрии и эксцесса равны нулю (подробнее рассмотрим это свойство
в следующем параграфе о приближенном методе проверки нормальности распределения).

Изменения среднего значения перемещают кривую функции плотности нормального распределения
в направлении оси Ox. Если
возрастает, кривая перемещается вправо, если
уменьшается, то влево.

Если меняется стандартное отклонение, то меняется высота вершины кривой. При увеличении
стандартного отклонения вершина кривой находится выше, при уменьшении — ниже.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

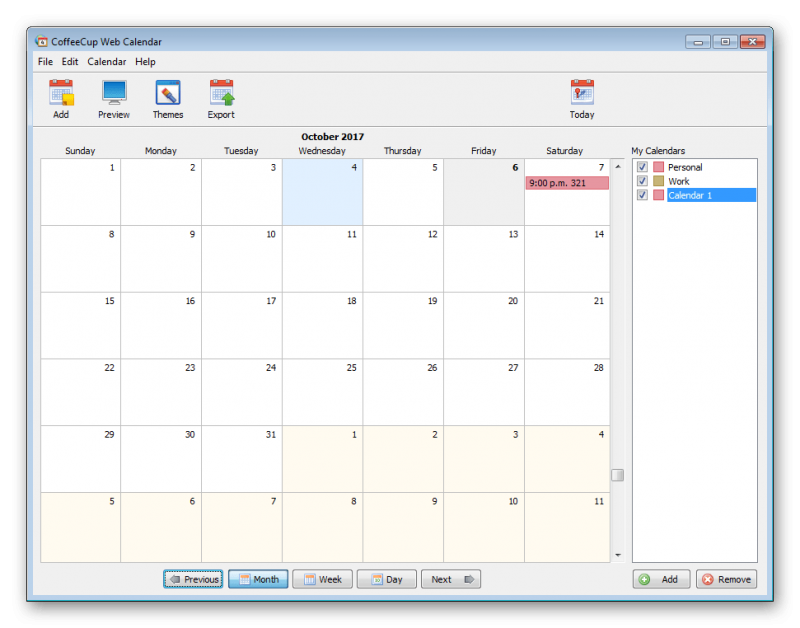
Построение гистограмм распределения в Excel

Суббота, 21 Ноября 2015 г. 22:58 + в цитатник

В связи с написанием диплома тема подсчёта статистики для меня крайне актуальна, посему делюсь найденной крайне полезной стаейкой по построению гистограмм распределения. Точнее частью этой статьи с наипростейшим алгоритмом постороения этих гистограмм Excel. Лично я строю этим способом гистограммы распределения значений показателей психологических тестов, ну а там уж каждому по потребностям, распределение чего надо посмотреть.

В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: естественно, в первую очередь я скажу, что металлургии, а также в экономике, биологии, политике, социологии и. много где еще. Статья эта будет, как несложно догадаться по ее названию, про использование некоторых средств статистического анализа, а именно — гистограммам. Ну, поехали.

Статистический анализ в Excel можно осуществлять двумя способами: • С помощью функций • С помощью средств надстройки «Пакет анализа». Ее, как правило, еще необходимо установить.

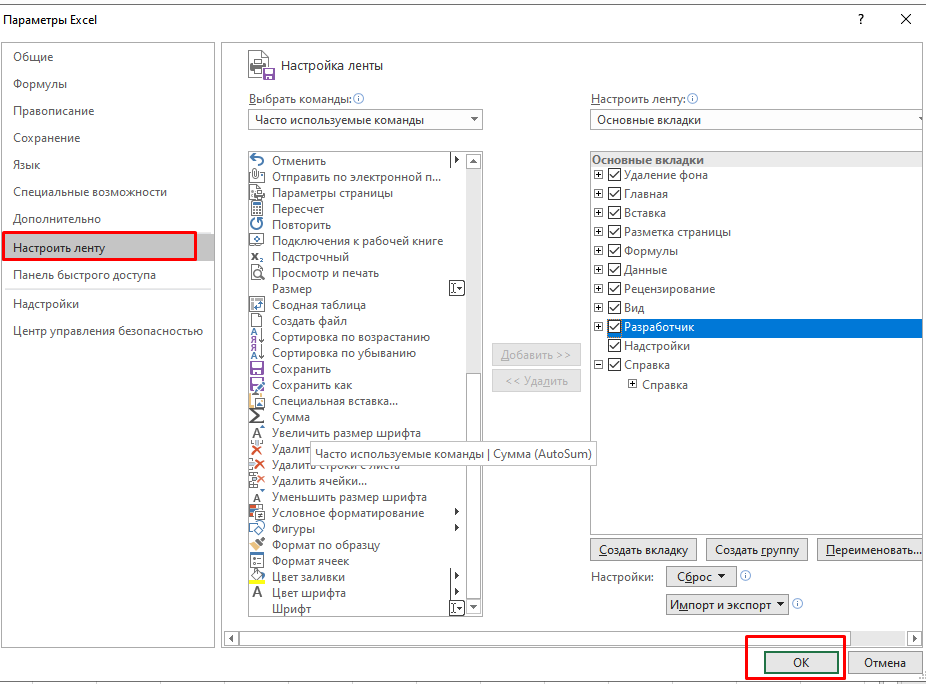
Чтобы установить пакет анализа в Excel, выберите вкладку «Файл» (а в Excel 2007 это круглая цветная кнопка слева сверху), далее — «Параметры», затем выберите раздел «Надстройки». Нажмите «Перейти» и поставьте галочку напротив «Пакет анализа».

А теперь — к построению гистограмм распределения по частоте и их анализу.

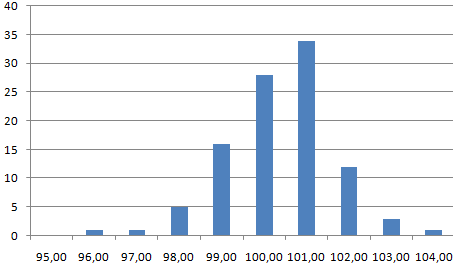
Речь пойдет именно о частотных гистограммах, где каждый столбец соответствует частоте появления* значения в пределах границ интервалов. Например, мы хотим посмотреть, как у нас выглядит распределение значения предела текучести стали S355J2 в прокате толщиной 20 мм за несколько месяцев. В общем, хотим посмотреть, похоже ли наше распределение на нормальное (а оно должно быть таким).

*Примечание: для металловедческих целей типа оценки размера зерна или оценки объемной доли частиц этот вид гистограмм не пойдет, т.к. там высота столбика соответствует не частоте появления частиц определенного размера, а доле объема (а в плоскости шлифа — площади), которую эти частицы занимают.

График нормального распределения выглядит следующим образом:

График функции Гаусса

Мы знаем, что реально такой график может быть получен только при бесконечно большом количестве измерений. Реально же для конечного числа измерений строят гистограмму, которая внешне похожа на график нормального распределения и при увеличении количества измерений приближается к графику нормального распределения (распределения Гаусса).

Построение гистограмм с помощью программ типа Excel является очень быстрым способом проверки стабильности работы оборудования и добросовестности коллектива: если получим «кривую» гистограмму, значит, либо прибор не исправен или мы данные неверно собрали, либо кто-то где-то преднамеренно мухлюет или же просто неверно использует оборудование.

А теперь — построение гистограмм!

Способ 1-ый. Халявный.

Идем во вкладку «Анализ данных» и выбираем «Гистограмма».
Выбираем входной интервал.
Здесь же предлагается задать интервал карманов, т.е. те диапазоны, в пределах которых будут лежать наши значения. Чем больше значений в интервале — тем выше столбик гистограммы. Если мы оставим поле «Интервалы карманов» пустым, то программа вычислит границы интервалов за нас.
Если хотим сразу же вывести график,то ставим галочку напротив «Вывод графика».
Нажимаем «ОК».
Вот, вроде бы, и все: гистограмма готова. Теперь нужно сделать так, чтобы по вертикальной оси отображалась не абсолютная частота, а относительная.
Под появившейся таблицей со столбцами «Карман» и «Частота» под столбцом «Частота» введем формулу «=СУММ» и сложим все абсолютные частоты.
К появившейся таблице со столбцами «Карман» и «Частота» добавим еще один столбец и назовем его «Относительная частота».
Во всех ячейках нового столбца введем формулу, которая будет рассчитывать относительную частоту: 100 умножить на абсолютную частоту (ячейка из столбца «частота») и разделить на сумму, которую мы вычислил в п. 7.

На какие вопросы отвечает гистограмма распределения?

Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.

В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.

«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»

Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:

Значение

Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному

Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.

Распределения

С практической точки зрения, мы можем думать о распределении как о функции, которая описывает связь между наблюдениями в пространстве выборки.

Например, нас может интересовать возраст людей: отдельные возрасты представляют наблюдения в данной области, а возрасты от 0 до 125 — размер пространства выборки. Распределение — это математическая функция, которая описывает взаимосвязь наблюдений разных высот.

— Страница 6,Статистика на простом английскомТретье издание, 2010.

Многие данные соответствуют хорошо известным и понятным математическим функциям, таким как распределение Гаусса. Функция может соответствовать данным с модификацией параметров функции, таких как среднее значение и стандартное отклонение в случае гауссиана.

Как только функция распределения известна, ее можно использовать в качестве краткого описания для описания и вычисления связанных величин, таких как вероятности наблюдений, и построения графика отношений между наблюдениями в домене.