Мастер-класс «использование кругов эйлера для развития логического мышления дошкольников»

Архив записей

Архив записейВыберите месяц Сентябрь 2020  (1) Август 2020  (2) Июль 2020  (2) Июнь 2020  (2) Декабрь 2019  (3) Ноябрь 2019  (4) Октябрь 2019  (3) Сентябрь 2019  (2) Май 2019  (1) Октябрь 2018  (1) Июнь 2018  (1) Апрель 2018  (1) Январь 2018  (1) Ноябрь 2017  (1) Октябрь 2017  (1) Сентябрь 2017  (2) Август 2017  (4) Июль 2017  (5) Июнь 2017  (4) Май 2017  (5) Апрель 2017  (2) Март 2017  (1) Февраль 2017  (1) Январь 2017  (3) Декабрь 2016  (1) Ноябрь 2016  (2) Октябрь 2016  (3) Сентябрь 2016  (4) Август 2016  (6) Июль 2016  (9) Июнь 2016  (4) Май 2016  (5) Апрель 2016  (6) Март 2016  (5) Февраль 2016  (8) Январь 2016  (8) Декабрь 2015  (9) Ноябрь 2015  (4) Июль 2015  (1) Март 2015  (1) Февраль 2015  (1) Январь 2015  (1) Июль 2014  (1) Июль 2013  (1) Март 2013  (2) Декабрь 2012  (1) Ноябрь 2012  (1) Сентябрь 2012  (3) Август 2012  (4) Июль 2012  (4) Июнь 2012  (4) Май 2012  (4) Апрель 2012  (5) Март 2012  (7) Февраль 2012  (8) Январь 2012  (7) Декабрь 2011  (5) Ноябрь 2011  (1)

Для чего нужны круги Эйлера

Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.

Есть несколько групп кругов Эйлера:

• равнозначные круги (рисунок 1 на схеме);
• пересекающиеся круги (рисунок 2 на схеме);
• подчиненные круги (рисунок 3 на схеме);
• соподчиненные круги (рисунок 4 на схеме);
• противоречащие круги (рисунок 5 на схеме);
• противоположные круги (рисунок 6 на схеме).

Посмотрите схему:

Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:

Круги, описывающие объединения понятий и демонстрирующие вложенность одного в другое. Посмотрите пример:

Круги, описывающие пересечения разных множеств, имеющих некоторые общие признаки. Посмотрите пример:

Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.

Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).

Решение логической содержательной задачи с помощью диаграмм Эйлера-Венна

Пример 2

Задача.

За зимние каникулы из $36$ учеников класса $2$ не были ни в кино, ни в театре, ни в цирке. В кино сходило $25$ человек, в театр — $11$, в цирк — $17$ человек; и в кино, и в театре — $6$; и в кино и в цирк — $10$; и в театр и в цирк — $4$.

Сколько человек побывало и в кино, и в театре, и в цирке?

Решение:

Обозначим количество ребят, побывавших и в кино, и в театре, и в цирке — $x$.

Построим диаграмму и узнаем количество ребят в каждой области:

Рисунок 9.

Не были ни в театре, ни в кино, ни в цирке — $2$ чел.

Значит, $36 — 2 = 34$ чел. побывали на мероприятиях.

В кино и театр сходило $6$ чел., значит, только в кино и театр ($6 — x)$ чел.

В кино и цирк сходило $10$ чел., значит, только в кино и цирк ($10 — x$) чел.

В театр и цирк сходило $4$ чел., значит, только в театре и цирк ($4 — x$) чел.

В кино сходило $25$ чел., значит, из них только в кино сходило $25 — (10 — x) — (6 — x) — x = (9+x)$.

Аналогично, только в театр сходило ($1+x$) чел.

Только в цирк сходило ($3+x$) чел.

Итак, сходили в театр, кино и цирк:

$(9+x)+(1+x)+(3+x)+(10-x)+(6-x)+(4-x)+x = 34$;

$33+x = 34$;

$x = 1$.

Т.е. только один человек сходил и в театр, и в кино, и в цирк.

Ответ: $1$.

Типичный пример кругов Эйлера

Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером

Обратите внимание на нижеследующий рисунок:. На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек

Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек

На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.

Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.

По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).

Пример решения задачи с помощью кругов Эйлера

58 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32 – трамвай, 44 – автобус. 21 человек из них используют метро и трамвай, 31 – метро и автобус, 22 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу?

Тут нужно понимать, что если сказано, что «42 человека используют метро», то это вовсе не означает, что кроме метро они не используют никаких других видов транспорта. Кто-нибудь из них может быть и использует. Может быть ещё какой-то один вид транспорта, трамвай или автобус. А может и сразу оба! Вопрос задачи как раз и состоит в том, чтобы посчитать людей, которые используют все три вида транспорта.

С первого взгляда даже непонятно, с чего начинать решение. Но если немного поразмыслить, становится ясно, что действовать нужно по следующему алгоритму. Будем стараться расписать всех людей (58 человек) через известные из условия данные. Нам известно, что автобус используют 44 человека. Прибавим к этому количество людей, которые используют метро. Их всего 42 человек. С помощью кругов Эйлера эту операцию можно изобразить наглядно в следующем виде:

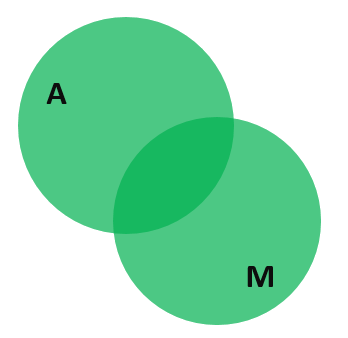
То есть пока что мы имеем дело с выражением 58 = 44 + 42… Знак «…» означает, что выражение ещё не закончено. Проблема в том, что мы посчитали людей на пересечении этих кругов дважды. Соответствующая область на диаграмме выделена тёмно-зелёным цветом. Поэтому один раз их нужно вычесть. Это люди, которые пользуются автобусом и метро. Их, как известно, 31. То есть наше «неоконченное» выражение принимает вид: 58 = 44 + 42 — 31… И на диаграмме при этом пропадает тёмно-зелёный цвет:

Пока всё хорошо. Прибавляем теперь людей, которые ездят на трамвае. Таких людей 32. Выражение принимает вид: 58 = 44 + 42 — 31 + 32… Диаграмма с кругами Эйлера, в свою очередь, становится следующей:

Проблема в том, что опять мы хватанули лишку. Люди, которых мы вновь посчитали дважды, отмечены на диаграмме тёмно-зелёным цветом. Эта область находится на пересечении множества, которое мы получили на предыдущем этапе, и множества людей, пользующихся трамваем.

Нужно вычесть людей, которых мы посчитали дважды. Но как это сделать? Единственное, что мы можем сделать, — это разом вычесть людей, которые передвигаются на трамвае и автобусе (их 22 человека), а также на трамвае и метро (таких людей 21). После этого наше неоконченное выражение для общего количества людей примет вид: 58 = 44 + 42 — 31 + 32 — 22 — 21…, а диаграмма с кругами Эйлера окажется с дыркой в центре, потому что центральную часть мы вычли дважды:

К счастью в незакрашенной области как раз и находятся те люди, число которых нам нужно посчитать. Действительно, эти бедняги используют ежедневно все три вида транспорта для того, чтобы добраться до работы, ведь они находятся на пересечении всех трёх множеств. Обозначим количество этих бедолаг за . Тогда диаграмма примет следующий вид:

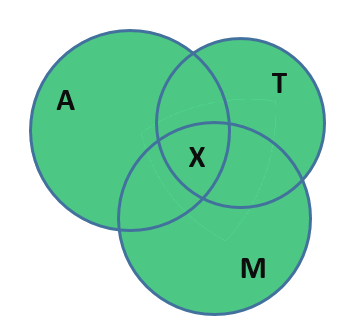
А уравнение станет следующим:

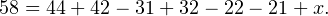
Расчёты дают . Это и есть ответ к задаче. Столько людей используют все три вида транспорта каждый день, чтобы добраться на работу.

Вот такое вот простое решение. Фактически, в одно уравнение. Просто удивительно, не правда ли?! А теперь представьте, как пришлось бы решать эту задачу без использования кругов Эйлера. Это было бы настоящее мучение. Так что в очередной раз убеждаемся, что любые методы визуализации чрезвычайно полезны при решении задач по математике. Используйте их, это поможет вам в решении сложных задач как на олимпиадах, так и на вступительных экзаменах по математике в лицеи и вузы.

Чтобы проверить, хорошо ли вы поняли решение данной задачи, ответьте на следующие вопросы:

1. Сколько человек используют только один вид транспорта для того, чтобы добраться до работы?
2. Сколько человек используют для этого ровно два вида транспорта?

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

• конечное, например, множество стран;
• бесконечное — множество звёзд во вселенной;
• пустое — множество острых углов в прямоугольнике.

В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:

• дополнение ¯A в калькуляторе имеет вид A’;
• пересечение A∩B представлено как A intersection B;
• объединение А⋃B обозначено A union B;
• симметрическая разность A∆B — symmetric difference of A and B;
• Относительное дополнение AB — AB.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

Дополнение множества

Дополнением к множеству A является множество \(\overline A\), которое состоит из элементов, не входящих в А. 

\(\overline A\;=\;\left\{x\;\vert\;x\;\not\in\;A\right\}\)

При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:

\(\overline A\;=\;U\;\backslash\;A\)

Таким образом выглядит дополнение \(\overline A\) графически:

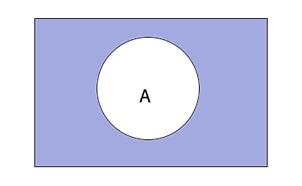
Отношения между множествами

Также следует различать понятия элементов и множества, объем которых отображают круги Эйлера. Понятие множества заимствовано из математической науки и имеет достаточно широкое значение. Примеры в логике и математике отображают его как некую совокупность объектов. Сами же объекты являются элементами данного множества. «Множество есть многое, мыслимое как единое» (Георг Кантор, основатель теории множеств).

Обозначение множеств осуществляется заглавными буквами: А, В, С, D… и т. д., элементов множеств – строчными: а, b, с, d…и др. Примерами множества могут быть студенты, находящиеся в одной аудитории, книги, стоящие на определенной полке (или, например, все книги в какой-либо определенной библиотеке), страницы в ежедневнике, ягоды на лесной поляне и т. д.

В свою очередь, если определенное множество не содержит ни одного элемента, то его называют пустым и обозначают знаком Ø. Например, множество точек пересечения параллельных прямых, множество решений уравнения х2 = -5.

Отношения между понятиями

Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.

Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

• равнозначные (тождественные);
• перекрещивающиеся;
• подчиняющие и подчинённые.

У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).

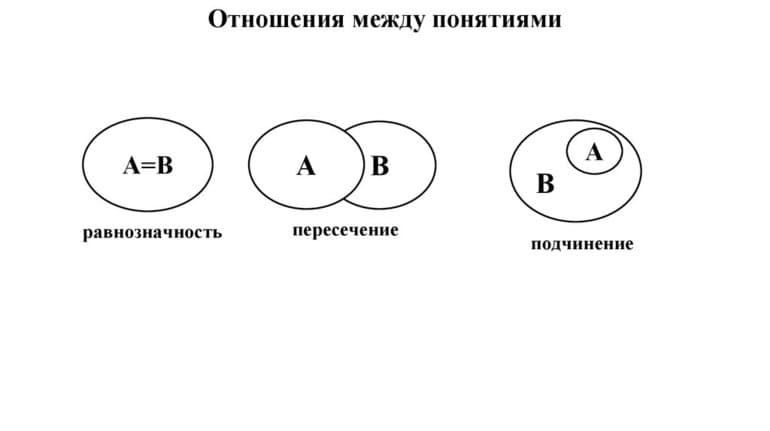
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.

Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».

Несовместимыми называют понятия, не имеющие общих элементов:

• соподчинённые;
• противоположные;
• противоречащие.

Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.

Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).

Объяснение заданий 17 ЕГЭ по информатике

17-я тема — «Логические выражения и запросы для поисковых систем» — характеризуется, как задания повышенного уровня сложности, время выполнения – примерно 2 минуты, максимальный балл — 1

Логические выражения и запросы для поисковых систем

• Таблицы истинности и порядок выполнения операций
• Поисковые запросы:
• операция «И» в поисковом запросе всегда ограничивает поиск (уменьшает количество страниц в выдаче), т. е., в ответ на запрос яблоко И груша поисковый сервер выдаст меньше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствуют оба этих слова;
• операция «ИЛИ» в поисковом запросе всегда расширяет поиск (увеличивает количество страниц в выдаче), т. е., в ответ на запрос яблоко ИЛИ груша поисковик выдаст больше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствует хотя бы одно из этих слов (или сразу оба слова);
• если в запросе присутствует фраза, заключенная в кавычки, то поисковик будет искать страницы с точно такой же фразой, а не просто отдельные слова из этой фразы; взятие словосочетания в кавычки ограничивает поиск, то есть, в ответ на запрос «яблоко груша» поисковик выдаст меньше страниц, чем на запрос яблоко груша, потому что поиск будет осуществляться только среди тех страниц, на которых эти слова стоят одно за другим.

Круги Эйлера

Большинство задач, связанных с поисковыми запросами, проще решать, используя круги Эйлера.

Пример использования кругов Эйлера:

Пример:
Известно количество сайтов, которых находит поисковый сервер по следующим запросам :

Ключевое слово	Количество сайтов, для которых данное слово является ключевым
Глинка & Лист	320
Бах & Лист	280
(Глинка | Бах) & Лист	430

Сколько сайтов будет найдено по запросу

Глинка & Бах & Лист

Задача с тремя кругами Эйлера

В классе 35 человек. Известно, что музыкой занимается 13 человек, танцами – 15 человек, плаванием – 20 человек, музыкой и танцами – 4 человека, музыкой и плаванием – 6 человек, плаванием и танцами – 7 человек, музыкой, плаванием и танцами – 1 человек. Есть ли в классе ученики, которые не увлекаются никакими из перечисленных занятий? Если да, то сколько их?

Итак, как же нам решить такую задачу? Те, кто с такими задачами сталкивался, знают, что их очень удобно решать с помощью так называемых кругов Эйлера.

Нам известно, что музыкой занимается 13 человек. Давайте изобразим этих людей с помощью круга, имея в виду, что все эти люди как бы находятся внутри этого круга. Чтобы это подчеркнуть, иногда даже ставят точки внутри этих кругов. Каждая точка символизирует человека. Но мы этого делать не будем. Лучше потом подпишем числами. Итак получаем вот такой круг:

Танцами занимается 15 человек. Это ещё один круг Эйлера. Причём! Он находится не где-то совершенно отдельно от первого, а в обязательном порядке пересекается с первым! Почему? Потому что мы знаем, что есть люди, которые занимаются и музыкой, и танцами. И на нашей диаграмме они должны быть расположены на пересечении этих кругов. Вот так:

Отлично! Теперь переходим к тем, кто занимается плаванием. Их ровно 20. То есть это ещё один «круг людей», который пересекается одновременно с первым кругом, потому что есть люди, занимающиеся музыкой и плаванием, и со вторым, так как есть люди, которые и плавают, и танцуют. То есть получается вот такая комбинация, содержащая 3 круга Эйлера:

Но как же решать задачу? Мы с вами ещё не использовали последнее условие. У нас есть такой уникально одарённый человек, который занимается одновременно и музыкой, и плаванием, и танцами. На нашей диаграмме он находится в том месте, где пересекаются все три круга. То есть в центре. И теперь давайте числами отмечать, сколько людей у нас находится в каждой из получившихся областей. Итак, в центральной части диаграммы у нас находится один человек:

Но тогда! Поскольку мы знаем, что музыкой и танцами занимается 4 человека, а в центральной области находится 1 человек, то в соседней правой области, как легко сообразить, находится человека:

Вычисляем теперь аналогично, сколько человек находится во всех областях на диаграмме, которые соседствуют с центральной. Поскольку музыкой и плаванием занимается 6 человек, то в области левее центральной находится ровно человек. Кроме того, если плаванием и танцами занимается 7 человек, то в области ниже центральной находится человек:

Очень хорошо! Но это ещё не всё. У нас остались белые пятна на диаграмме. Давайте их устраним. Как это сделать? Теперь вспоминаем, что музыкой увлекается 13 человек. Значит, в самой верхней части верхнего круга находится человека:

Аналогично, поскольку танцуют у нас 15 человек, то в самой правой части правого круга находится ровно человек. Ну и поскольку пловцов у нас 20, то в самой левой части левого круга находится ровно ребят. Итак, мы узнали, сколько и где у нас находится людей:

Ну а теперь… Чтобы узнать, сколько человек занимается хотя бы одном каким-то видом увлечений из перечисленных (музыкой, плаванием или танцами), нужно просто сложить все эти числа. Их сумма равна . Но всего в классе 35 человек. Это означает, что есть ровно человека, которые не увлекаются ни одним из перечисленных занятий. И это наш ответ.

Вот такая задача. Эта задача, кстати, была на вступительном экзамене в лицей №1580 в 2018 году. Её решали шестиклассники, которые поступали, соответственно, в 7 класс этого лицея. Я являюсь репетитором по математике и физике и готовлю школьников к вступительным экзаменам в различные школы Москвы, в том числе в лицей 1580. Если вам требуется такая подготовка, обращайтесь ко мне. Мой контакты вы найдёте на этой странице.

Ход занятия:

1. «Необычное приветствие» Звучит музыка дети входят в зал. Психолог предлагает детям встать в круг: «Ребята. Наше занятие мы начнем с необычного приветствия. Давайте поздороваемся друг с другом глазками. А теперь носиками, и подарим друг другу улыбку.Психолог: Сегодня мы с вами отправляемся в путешествие в очень удивительную и сказочную страну под названием «Вундеркиндию» но путь к ней будет нелегкий, по пути к ней нас ждут интересные испытания, увлекательные и творческие задания. А поможет нам в пути карта схема на которой изображен весь путь к далекой стране.

2.Город Близнецов: Ребят встречают два близнеца и говорят «Здравствуйте ребята, вы попали в город Близнецов. Где живут близнецы и близняшки все они на первый раз одинаковы. но это не так. Вот вам первое испытание найти все отличия между близняшками.

З. На полу нарисованы пропасть «Беспамятства». А через нее сделан мостик. У пропасти стоит хранитель «Здравствуйте ребята. Я хранитель и стою здесь для, того, чтобы путники не упали в эту пропасть. Но просто так я вас пропустить не могу. Только у тех у кого хорошая память и яркое воображение пройдет через эту пропасть, закройте глаза. Я скажу вам слово, а вы запомните какие образы у вас появились в голове.

Игра ассоциации:

Путешествие-

Дружба-

Веселье-

Ум-

Терпение-

Удача-

2. Страна «Сообразилия».Ребят встречает взрослый в костюме ученого: «Добро пожаловать в нашу страну умных и любознательных людей. Местные жители очень любят головоломки и вам предлагают необычное задание».

Задание с головоломкой Танграм, необходимо восстановить фотографию гуся, лисы.

Я- веселая лиса Мне вцепилась в хвост оса Я бедняжка так вертелась Что на части разлетелась 1 Помогите, помогите Из кусков меня сложите!

Золотой веселый гусь Ничего я не боюсь 1 Но вчера упал я с кочки Развалился на кусочки!

Помогите, помогите

Из кусков меня сложите!

Другим ребятам предлагается собрать фигуры по образцу квадрата Воскобовича

3. Дети попадают в волшебный лес. Неожиданно появляются гномики.

Песня с гномиками. (танцевальные движения под музыку)

Гномики подводят детей к дереву. Посреди леса стоит волшебное дерево на нем весит пакет с загадками.

Загадки: Стрекоза сидит не на цветке и не на листке. Кузнечик сидит не на грибке и не на цветке. Божья коровка сидит не на листке и не на грибке. Кто на чем сидит?

Белка, заяц и лиса жили в разных домиках. Белка жила не в красном и не синем домике. Заяц жил не не в красном и не в оранжевом домике. Догадайся, в каких домиках жили звери?

4. Игра головоломка — «Раздели зверят».

5. Сразу за волшебным лесом находится болото Лени. В нем сидят два ребенка, играя роль учеников лентяев. Они неопрятно одеты, не расчесаны.Они кричат и просят о помощи: «Помогите ребята, помогите нам выбраться из болота лени».

Задание «Загадочные круги».

И вот пришли мы в страну Вундеркиндию.Навстречу им выходит Знайка и говорит: «Молодцы ребята, что прошли все испытания и пришли в нашу страну, где живут умные и сообразительные жители и они для вас приготовили интересные задания».

Игра «А если что»:

Если командир в мундире, то мундир. на командире.

Если сапог на ноге, то нога. в сапоге Если карман на пиджаке, то пиджак. с карманом Если картина над столом, то стол. под картиной Если масло в каше, значит каша. с маслом Если Оля старше Коли, значит Коля. младше Оли.

Если стол выше стула, то стул. ниже стола.

Если река шире ручья, то ручей. уже реки.

Если велосипед едет медленнее мотоцикла, то мотоцикл едет. быстрее.

Если на небе тучи, значит скоро.

Если в воду добавить сахар, то.

Если в комнату принести снег, то.

Знайка: «Молодцы ребята»

И затем Знайка вручает памятные сувениры.

Происхождение термина

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Пока не очень понятно, верно? Посмотрите на этот рисунок:

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Автор метода — ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.

Примеры задач с решением

Задача

Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?

Решение

В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.

\(n(U)\;=\;100\\n(Р)\;=\;28,\;n(Ф)\;=\;42,\;n(К)\;=\;30\\n\;(Р\;\cap\;Ф)\;=\;10,\;n(Р\;\cap\;К)\;=\;8,\;n\;(Ф\;\cap\;К)\;=\;5\\n\;(Р\;\cap\;Ф\;\cap\;К)\;=\;3\)

Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)

В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна

Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено

Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.

\(n(Р\;\cup\;Ф\;\cup\;К)\;=\;13\;+\;7\;+\;30\;+5\;+\;3\;+\;2\:+\;20\;=\;80\)

Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:

\(n(U\;\backslash\;(Р\;\cup\;Ф\;\cup\;К))\;=\;100\;-\;80\;=\;20\)

Ответ: 20 туристов не побывали ни в одном из указанных заведений.

Задача

На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?

Решение

Начнем с определения множеств и введения обозначений. В данном случае, их три:

• множество задач по алгебре («А»);
• множество задач по геометрии («Г»);
• множество задач по тригонометрии («Т»).

Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.

Теперь используя диаграмму, обозначим область, которую необходимо найти:

Определим количество школьников для всех возможных областей.

Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».

Найдем остальные области:

1. Область А = 0, Г = 0, Т = 1: школьников нет.
2. Область А = 0, Г = 1, Т = 0: школьников нет.
3. Область А = 0, Г = 1, Т = 1: 100 школьников.
4. Область А = 1, Г = 0, Т = 0: школьников нет.
5. Область А = 1, Г = 0, Т = 1: 200 школьников.
6. Область А = 1, Г = 1, Т = 0: 300 школьников.
7. Область А = 1, Г = 1, Т = 1: 300 школьников.

Теперь внесем значения всех областей в диаграмму:

Определим x:

\(x\;=\;U\;-\;(A\;\cup\;Г\;\cup\;Т)\;\)

При U — универсум

U = 1000

\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)

x = 1000 — 900 = 100

Метамодель в виде кругов Эйлера

А теперь как раз давайте распределим паттерны нарушения метамодели по категориям. Как я уже сказал, по-видимому некоторые паттерны могут получаться при помощи нескольких процессов моделирования мира и, соответственно, восстанавливать информацию тоже можно разными способами.

Например, кванторы общности. Их можно отнести к обобщениям, и к опущениям. Просто нарушение при сверхобобщении может быть разных видов. У человека действительно был опыт, который он распространил на весь контекст: «Все женщины, с которыми у меня были отношения, меня бросали» (было 3-4 случая) => «Женщины всегда бросают» — это чистое обобщение, он не выкидывает какие-то куски опыта, просто расширяет личный опыт на «всех женщин» (создаёт общее правило) Но чаще при сверхобобщении человек ещё чего-то выкидывает, и оказывается, что из пяти «отношений», два заканчивал он сам, один раз расходились полюбовно, и только в двух случаях его бросали. Здесь сначала опущение, потом обобщение. Вывод при этом может быть точно таким же: «Женщины всегда бросают». И вопросы на исправление нарушения как раз будут относится к двум типам: «Все женщины всегда всех бросают?» — выход за границы, — «Были ли в твоей жизни женщины, которые тебя не бросали?» — восстановление опущения.

Аналогично с неспецифичными существительными и местоимениями. С одной стороны происходит обобщение — соседи сверху => люди, — с другой стороны теряется конкретная информация.

При утраченном перформативе при опускании автора мнения одновременно происходит обобщение: «Известно, что это не правильно».

Номинализации здесь относятся одновременно и к искажениями – потому что потеряна структура, — и к опущениям, потому что при «номинализировании» теряется информация о времени и направлении действия.

Имеется в виду, что у переходных глаголов есть направление действия: «Петя любит Веру», — после «номинализирования» превращается в «У Пети любовь с Верой»

Исправление нарушений метамодели

Для восстановления опущений обычно задаётся два основных вопроса: — Кто что с кем/чем сделал? – для восстанавления потерянных субъекта и/или объекта действия. — Как конкретно? – для уточнения информации. Для группы пересечения обобщения и опущения, можно проверить не выкинута ли какая полезная информация: — Было ли, когда было не так? Для выхода за границы и проверки обобщения можно либо проверить правильность обобщения: — Что действительно все/всегда/везде? Либо выясняем последствия выхода за границы: — Что будет, если ты это сделаешь/не сделаешь? Для восстановления структуры (исправления искажений) мы выясняем, на основе чего человек сделал этот вывод: — А с чего ты это взял? — Каким образом…? Либо просто предлагаем «восстановленный» вариант, как с номинализациями: любовь – любить, разговор – разговаривать.

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».

Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.