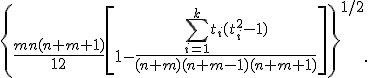Непараметрические методы сравнения двух выборок и их применение в r
Содержание:
Критерии и методы
ПАРНЫЙ t-КРИТЕРИЙ СТЬЮДЕНТА
Парный t-критерий Стьюдента – одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.
Уильям Госсет
1. История разработки t-критерия
t-критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется парный t-критерий Стьюдента?
Парный t-критерий Стьюдента используется для сравнения двух зависимых (парных) выборок. Зависимыми являются измерения, выполненные у одних и тех же пациентов, но в разное время, например, артериальное давление у больных гипертонической болезнью до и после приема антигипертензивного препарата. Нулевая гипотеза гласит об отсутствии различий между сравниваемыми выборками, альтернативная — о наличии статистически значимых различий.
3. В каких случаях можно использовать парный t-критерий Стьюдента?
Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.
Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.
Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.
4. Как рассчитать парный t-критерий Стьюдента?
Парный t-критерий Стьюдента рассчитывается по следующей формуле:
где Мd — средняя арифметическая разностей показателей, измеренных до и после, σd — среднее квадратическое отклонение разностей показателей, n — число исследуемых.
5. Как интерпретировать значение t-критерия Стьюдента?
Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p<0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
- Если рассчитанное значение парного t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного парного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
6. Пример расчета t-критерия Стьюдента
Для оценки эффективности нового гипогликемического средства были проведены измерения уровня глюкозы в крови пациентов, страдающих сахарным диабетом, до и после приема препарата. В результате были получены следующие данные:
| N пациента | Уровень глюкозы в крови, ммоль/л | |
| до приема препарата | после приема препарата | |
| 1 | 9.6 | 5.7 |
| 2 | 8.1 | 4.2 |
| 3 | 8.8 | 6.4 |
| 4 | 7.9 | 5.5 |
| 5 | 9.2 | 5.3 |
| 6 | 8.0 | 4.2 |
| 7 | 8.4 | 5.1 |
| 8 | 10.1 | 5.9 |
| 9 | 7.8 | 7.5 |
| 10 | 8.1 | 5.0 |
Решение:
1. Рассчитаем разность каждой пары значений (d):
| N пациента | Уровень глюкозы в крови, ммоль/л | Разность значений (d) | |
| до приема препарата | после приема препарата | ||
| 1 | 9.6 | 5.7 | 3.9 |
| 2 | 8.1 | 5.4 | 2.7 |
| 3 | 8.8 | 6.4 | 2.4 |
| 4 | 7.9 | 5.5 | 2.4 |
| 5 | 9.2 | 5.3 | 3.9 |
| 6 | 8.0 | 5.2 | 2.8 |
| 7 | 8.4 | 5.1 | 3.3 |
| 8 | 10.1 | 6.9 | 3.2 |
| 9 | 7.8 | 7.5 | 2.3 |
| 10 | 8.1 | 5.0 | 3.1 |
2. Найдем среднюю арифметическую разностей по формуле:
3. Найдем среднее квадратическое отклонение разностей от средней по формуле:
4. Рассчитаем парный t-критерий Стьюдента:
5. Сравним полученное значение t-критерия Стьюдента 8.6 с табличным значением, которое при числе степеней свободы f равном 10 — 1 = 9 и уровне значимости p=0.05 составляет 2.262. Так как полученное значение больше критического, делаем вывод о наличии статистически значимых различий содержания глюкозы в крови до и после приема нового препарата.
Описание критерия
Заданы две выборки 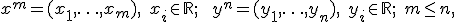 в противном случае следует поменять выборки местами.
в противном случае следует поменять выборки местами.
Дополнительные предположения: обе выборки простые, объединённая выборка независима;
Вычисление статистики критерия:
- Построить общий вариационный ряд объединённой выборки и найти ранги всех элементов обеих выборок в общем вариационном ряду.
- Рассчитать суммы рангов, соответствующих обеим выборкам:
- Если размеры выборок совпадают (), то значение статистики будет равняется одной из сумм рангов или (любой). Если же выборки не равны, то , то есть сумме рангов, соответствующей меньшей выборке. Заметим, что статистика линейно связана со статистикой U-критерия Манна-Уитни.
Критерий (при уровне значимости ):
Против альтернативы :
- если , то нулевая гипотеза отвергается. Здесь есть -квантиль табличного распределения Уилкоксона с параметрами .
Асимптотический критерий:
Критическая область двухвыборочного критерия Уилкоксона (нормальная аппроксимация).
Рассмотрим нормированную и центрированную статистика Уилкоксона:
- ;
асимптотически имеет стандартное нормальное распределение. Нулевая гипотеза (против альтернативы ) отвергается, если , где есть -квантиль стандартного нормального распределения.
Приближение можно использовать, если размер хотя бы одной из выборок превышает 25. Если размеры выборок равны, то данная аппроксимация хорошо работает до .
Случай совпадающих наблюдений:
При наличии связок необходимо учесть их с помощью поправки. Выражение в знаменателе необходимо заменить на следующее:
- Здесь — количество только тех связок, в которые входят ранги как одной, так и другой выборок, — их размеры. Совпадения, целиком состоящие из элементов одной и той же выборки, на величину не влияют. Наблюдения, не совпадающие с другими, рассматриваются как связки размера 1. Для элементов связок вычисляется средний ранг.
Поправка:
В 1976 году Р. Иман предложил следующую аппроксимацию, обеспечивающую значительное снижение относительной ошибки для критических значений, в том числе на малых выборках. Поправка использует полусумму нормальной и стьюдентовской квантилей. Положим . Тогда:
- .
Гипотеза отвергается, если , где обозначают соответственно квантили уровня стандартного нормального распределения и распределения Стьюдента с степенью свободы.
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.

Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.

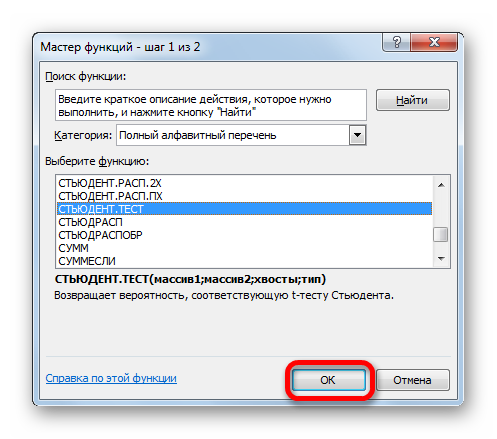
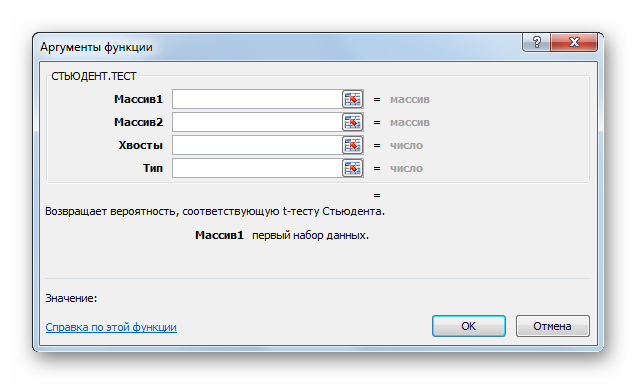
Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».

Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.

Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».

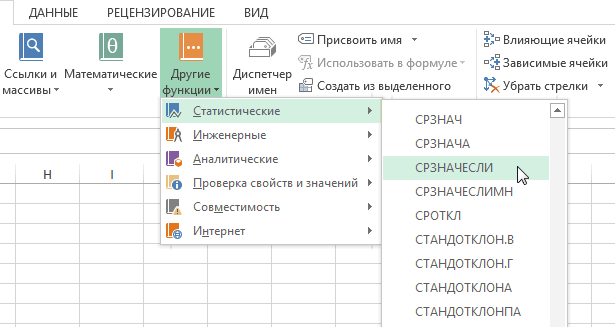
Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».

Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.

После того, как данные введены, жмем кнопку Enter для вывода результата на экран.

Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Назначение Т — критерия Вилкоксона
Критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых.
Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.
Описание Т – критерия Вилкоксона
Этот критерий применим в тех случаях, когда признаки измерены по крайней мере по шкале порядка, и сдвиги между вторым и первым замерами тоже могут быть упорядочены. Для этого они должны варьировать в достаточно широком диапазоне. В принципе, можно применять Т — критерий Вилкоксона и в тех случаях, когда сдвиги принимают только три значения: -1, 0 и +1, но тогда критерий Т вряд ли добавит что-нибудь новое к тем выводам, которые можно было бы получить с помощью критерия знаков. Вот если сдвиги изменяются, скажем, от -30 до +45, тогда имеет смысл их ранжировать и потом суммировать ранги.
Суть метода состоит в том, что мы сопоставляем выраженность сдвигов в том и ином направлениях по абсолютной величине. Для этого мы сначала ранжируем все абсолютные величины сдвигов, а потом суммируем ранги. Если сдвиги в положительную и в отрицательную сторону происходят случайно, то суммы рангов абсолютных значений их будут примерно равны. Если же интенсивность сдвига в одном из направлений перевешивает, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
Первоначально мы исходим из предположения о том, что типичным сдвигом будет сдвиг в более часто встречающемся направлении, а нетипичным, или редким, сдвигом — сдвиг в более редко встречающемся направлении.
Гипотезы Т – критерия Вилкоксона
H: Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении.
H1: Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении.
Ограничения в применении Т – критерия Вилкоксона
1. Минимальное количество испытуемых, прошедших измерения в двух условиях — 5 человек. Максимальное количество испытуемых — 50 человек, что диктуется верхней границей имеющихся таблиц.
2. Нулевые сдвиги из рассмотрения исключаются, и количество наблюдений n уменьшается на количество этих нулевых сдвигов (при условии, если флажок «Учитывать нулевой сдвиг?» не установлен). Можно обойти это ограничение (установив флажок «Учитывать нулевой сдвиг?»), сформулировав гипотезы, включающие отсутствие изменений, например: «Сдвиг в сторону увеличения значений превышает сдвиг в сторону уменьшения значений и тенденцию сохранения их на прежнем уровне».
Автоматический расчет Т — критерия Вилкоксона
Шаг 1
Введите в первую колонку данные первого замера («До»), а во вторую колонку данные второго замера («После»). Данные вводятся по одному числу на строку; без пробелов, пропусков и т.д. Вводятся только цифры. Дробные числа вводятся со знаком «.» (точка). После заполнения колонок нажмите на кнопку «Шаг 2», чтобы произвести расчет Т-критерия Вилкоксона.
Тест Уилкоксона со знаком
В некоторых случаях образцы данных могут быть сопряжены.
Есть много причин, почему это может иметь место, например, образцы связаны илив некотором родеили представляют два измерения одного и того же метода. Более конкретно, каждая выборка является независимой, но происходит из одной популяции.
Примерами парных выборок в машинном обучении могут быть один и тот же алгоритм, оцениваемый на разных наборах данных, или разные алгоритмы, оцениваемые на одних и тех же данных обучения и испытаний.
Образцы не являются независимыми, поэтому U-критерий Манна-Уитни не может быть использован. Вместо этогоЗнак Вилкоксонаиспользуется, также называемый тестом Уилкоксона, названный в честь Фрэнка Уилкоксона. Это эквивалент парного T-критерия Стьюдента, но для ранжированных данных вместо реальных данных с гауссовым распределением.
— страницы 38-39,Непараметрическая статистика для нестатиков: пошаговый подход, 2009.
Предположение по умолчанию для теста, нулевая гипотеза, состоит в том, что два образца имеют одинаковое распределение.
- Не в состоянии отклонить H0: Распределения выборки равны.
- Отклонить H0: Распределения выборки не равны.
Для того чтобы тест был эффективным, требуется не менее 20 наблюдений в каждой выборке данных.
Тест со знаком ранга Уилкоксона может быть реализован в Python с использованиемфункция wilcoxon () SciPy, Функция берет две выборки в качестве аргументов и возвращает вычисленную статистику и значение p.
Ниже приведен полный пример, демонстрирующий вычисление критерия Уилкоксона со знаком для задачи теста. Два образца технически не спарены, но мы можем притвориться, что они ради демонстрации вычисления этого теста значимости.
Выполнение примера вычисляет и печатает статистику и печатает результат.
Значение р сильно интерпретируется, что позволяет предположить, что выборки взяты из разных распределений.
U-тест Манна-Уитни
U-критерий Манна-Уитни — это непараметрический критерий статистической значимости для определения того, были ли взяты две независимые выборки из популяции с одинаковым распределением.
Тест был назван по имени Генри Манна и Дональда Уитни, хотя его иногда называют тестом Уилкоксона-Манна-Уитни, также названным по имени Фрэнка Уилкоксона, который также разработал вариант теста.
— страница 58,Непараметрическая статистика для нестатиков: пошаговый подход, 2009.
Предположение по умолчанию или нулевая гипотеза заключается в том, что нет различий между распределениями выборок данных. Отказ от этой гипотезы позволяет предположить, что между образцами, вероятно, существует некоторое различие. Более конкретно, тест определяет, одинаково ли вероятно, что любое случайно выбранное наблюдение из одной выборки будет больше или меньше, чем выборка из другого распределения. Если нарушено, это предлагает отличающиеся распределения.
- Не в состоянии отклонить H0: Распределения выборки равны.
- Отклонить H0: Распределения выборки не равны.
Для того чтобы тест был эффективным, требуется не менее 20 наблюдений в каждой выборке данных.
Мы можем реализовать U-тест Манна-Уитни в Python, используяmannwhitneyu () функция SciPy, Функции принимают в качестве аргументов два образца данных. Возвращает статистику теста и значение p.
В приведенном ниже примере демонстрируется U-критерий Манна-Уитни для набора тестовых данных.
При выполнении примера вычисляется тест для наборов данных и выводится статистика и значение p.
Значение р сильно говорит о том, что выборочные распределения отличаются, как и ожидалось.
Непараметрические тесты статистической значимости
Непараметрическая статистикаэто те методы, которые не предполагают конкретного распределения данных.
Часто они относятся к статистическим методам, которые не предполагают гауссово распределение. Они были разработаны для использования с порядковыми или интервальными данными, но на практике их также можно использовать для ранжирования реальных наблюдений в выборке данных, а не на самих значениях наблюдений.
Общий вопрос о двух или более наборах данных заключается в том, отличаются ли они. В частности, является ли статистически значимым различие между их центральной тенденцией (например, среднее значение или медиана).
На этот вопрос можно ответить для выборок данных, которые не имеют гауссова распределения, с помощью непараметрических критериев статистической значимости. Нулевой гипотезой этих тестов часто является предположение, что обе выборки были взяты из популяции с одинаковым распределением и, следовательно, с одинаковыми параметрами популяции, такими как среднее значение или медиана.
Если после расчета критерия значимости для двух или более выборок нулевая гипотеза отклоняется, это указывает на наличие свидетельств, позволяющих предположить, что выборки были взяты из разных групп населения, и, в свою очередь, различие между выборочными оценками параметров совокупности, таких как средние или медианы может быть значительным.
Эти тесты часто используются на выборках оценок моделей, чтобы подтвердить, что разница в навыках между моделями машинного обучения значительна.
В целом, каждый тест вычисляет статистику теста, которая должна интерпретироваться с некоторой подготовкой в статистике и более глубокими знаниями самого статистического теста. Тесты также возвращают значение p, которое можно использовать для интерпретации результата теста. Значение p можно рассматривать как вероятность наблюдения двух выборок данных с учетом базового предположения (нулевая гипотеза), что две выборки были взяты из совокупности с одинаковым распределением.
Значение p можно интерпретировать в контексте выбранного уровня значимости, называемого альфа. Общее значение для альфа составляет 5% или 0,05. Если значение p ниже уровня значимости, то тест говорит, что имеется достаточно доказательств, чтобы отвергнуть нулевую гипотезу, и что выборки, вероятно, были взяты из популяций с различным распределением.
- p & lt; = альфа: отклонить H0, другое распределение.
- p & gt; альфа: не удается отклонить H0, то же распределение.
Kruskal-Wallis H Test
При работе с тестами значимости, такими как тесты Манн-Уитни U и Уилкоксона, сравнения выборок данных должны выполняться попарно
Это может быть неэффективно, если у вас много выборок данных, и вас интересует только, имеют ли два или более выборок различное распределение.
Тест Крускала-Уоллиса является непараметрической версией одностороннего дисперсионного анализа или ANOVA для краткости. Он назван в честь разработчиков метода Уильяма Крускала и Уилсона Уоллиса. Этот тест можно использовать для определения того, имеют ли более двух независимых выборок различное распределение. Его можно рассматривать как обобщение U-критерия Манна-Уитни.
Предположение по умолчанию или нулевая гипотеза состоит в том, что все выборки данных были взяты из одного и того же распределения. Именно то, что медианы населения всех групп равны. Отказ от нулевой гипотезы указывает на то, что имеется достаточно доказательств, чтобы предположить, что один или несколько образцов доминируют над другим образцом, но тест не указывает, какие образцы или в каком количестве.
— страница 100,Непараметрическая статистика для нестатиков: пошаговый подход, 2009.
- Не в состоянии отклонить H0: Все примеры распределений одинаковы.
- Отклонить H0: Одно или несколько примеров распределений не равны.
Каждая выборка данных должна быть независимой, иметь 5 или более наблюдений, а выборки данных могут отличаться по размеру.
Мы можем обновить тестовую задачу, чтобы иметь 3 выборки данных вместо 2, два из которых имеют одинаковое среднее значение выборки. Учитывая, что один образец отличается, мы ожидаем, что тест обнаружит разницу и отвергнет нулевую гипотезу.
H-тест Крускала-Уоллиса может быть реализован в Python с использованиемфункция kruskal () SciPy, Он принимает две или более выборки данных в качестве аргументов и возвращает статистику теста и значение p в качестве результата.
Полный пример приведен ниже.
Выполнение примера вычисляет тест и печатает результаты.
Значение p интерпретируется, правильно отвергая нулевую гипотезу о том, что все выборки имеют одинаковое распределение.
Критерий Уилкоксона
Начнем знакомство с непараметрических тестов для зависимых выборок. Прежде всего стоит отметить, что выборки называются зависимыми, когда испытуемые одной и той же группы были протестированы в разные моменты времени с меняющимися (1) или неменяющимися (2) условиями эксперимента. В первом случае проверяется эффект какого либо действия в сравнении с контрольным измерением («до и после»), во втором — повторяемость результатов эксперимента («контроль-повтор»).
Тест Уилкоксона (от английского «Wilcoxon signed-rank test») является широко используемым и эффективным методом выявления различий между медианами двух зависимых выборок с распределением данных отличным от нормального. Он идеально подходит для сравнения маленьких выборок, где количество испытуемых/исследований больше 5, но меньше 50. Как и для всех критериев, рассмотренных в этой статье, данные могут быть как количественными, так и порядковыми. Метод был разработан в 1945 году американским статистиком и химиком Фрэнком Уилкоксоном (фото справа).
Чтобы запустить тест Уилкоксона в среде R следует загрузить данные выборок и ввести следующую команду:
Как и в t-тесте, в непараметрических статистических тестах внутри скобок можно добавить дополнительные параметры, такие как alternative, conf.int, conf.level. Чтобы посмотреть все аргументы функции, поставьте перед ней знак вопроса, в нашем случае: ?wilcox.test
Критерии и методы
U-КРИТЕРИЙ МАННА-УИТНИ
Фрэнк Уилкоксон
U-критерий Манна-Уитни – непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
1. История разработки U-критерия
Данный метод выявления различий между выборками был предложен в 1945 году американским химиком и статистиком Фрэнком Уилкоксоном.В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H.B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.
 Хенри Манн
Хенри Манн
2. Для чего используется U-критерий Манна-Уитни?
U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.
3. В каких случаях можно использовать U-критерий Манна-Уитни?
U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.
U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти.
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.
Аналогом U-критерия Манна-Уитни для сравнения трех и более групп является Критерий Краскела-Уоллиса.
4. Как рассчитать U-критерий Манна-Уитни?
Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд, путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.
Например, две единицы, занимающие в едином ранжированном ряду 2 и 3 место (ранг), имеют одинаковые значения. Следовательно, каждой из них присваивается ранг равный (3 + 2) / 2 = 2,5.
В составленном едином ранжированном ряду общее количество рангов получится равным:
где n1 — количество элементов в первой выборке, а n2 — количество элементов во второй выборке.
Далее вновь разделяем единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок, запоминая при этом значения рангов для каждой единицы. Подсчитываем отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определяем большую из двух ранговых сумм (Tx) соответствующую выборке с nx элементами.
Наконец, находим значение U-критерия Манна-Уитни по формуле:
5. Как интерпретировать значение U-критерия Манна-Уитни?
Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) с критическим значением U при заданной численности сопоставляемых выборок:
- Если полученное значение U меньше табличного или равно ему, то признается статистическая значимость различий между уровнями признака в рассматриваемых выборках (принимается альтернативная гипотеза). Достоверность различий тем выше, чем меньше значение U.
- Если же полученное значение U больше табличного, принимается нулевая гипотеза.