Логические выражения

Как этот закон работает в контексте истории?

С точки зрения диалектического отрицания переход к социализму из отношений частной собственности, заменившей первобытно-общинную собственность, означал больше, чем «кажущееся возвращение к старому», то есть повторение некоторых существенных элементов старого на другом, значительно более развитом фундаменте. Он также означал переход к новому циклу с существенно разными внутренними противоречиями и законами движения.

Последовательность циклов, составляющих цепочку развития, может быть представлена ​​как спираль. Развитие, которое словно повторяется, этапы, которые уже были пройдены. Мы словно повторяем их, но по-другому, на более высоком уровне, развитие происходит, если можно так выразиться, вверх, а не просто по прямой.

В таком представлении каждый цикл имеет один оборот, один поворот по спирали развития, а сама спираль — цепь циклов. Хотя спираль — это всего лишь изображение, представляющее связь между двумя или более пунктами в процессе развития, она фиксирует общее направление развития, которое происходит в соответствии с законом отрицания отрицания.

Возвращение к тому, что уже прошло, не является полным возвратом: развитие не повторяет уже пройденные пути, но ищет новые, которые соответствуют измененным внешним и внутренним условиям. Чем сложнее процесс развития, тем более относительным является повторение определенных свойств или характеристик, встречающихся на предыдущих этапах. Спираль характеризует не только форму, но и темп развития. С каждым новым поворотом или заворотом спирали позади остается еще более значительный путь. Таким образом, можно сказать, что процесс развития связан с ускорением темпа и постоянным изменением внутреннего временного масштаба развивающейся системы. Эта закономерность встречается в развитии научных знаний, а также в развитии общества и природы.

Операции со сравнениями

Сравнения по одному и тому же модулю обладают многими свойствами обычных равенств. Например, их можно складывать, вычитать и перемножать: если числа a1,a2,…,an{\displaystyle a_{1},a_{2},\ldots ,a_{n}} и b1,b2,…,bn{\displaystyle b_{1},b_{2},\ldots ,b_{n}} попарно сравнимы по модулю m{\displaystyle m}, то их суммы a1+a2+…+an{\displaystyle a_{1}+a_{2}+\ldots +a_{n}} и b1+b2+…+bn{\displaystyle b_{1}+b_{2}+\ldots +b_{n}}, а также произведения a1⋅a2⋅…⋅an{\displaystyle a_{1}\cdot a_{2}\cdot …\cdot a_{n}} и b1⋅b2⋅…⋅bn{\displaystyle b_{1}\cdot b_{2}\cdot …\cdot b_{n}} тоже сравнимы по модулю m{\displaystyle m}:

(a1+a2+…+an)≡(b1+b2+…+bn)(modm);{\displaystyle (a_{1}+a_{2}+\ldots +a_{n})\equiv (b_{1}+b_{2}+\ldots +b_{n}){\pmod {m}};}

(a1⋅a2⋅…⋅an)≡(b1⋅b2⋅…⋅bn)(modm).{\displaystyle (a_{1}\cdot a_{2}\cdot \ldots \cdot a_{n})\equiv (b_{1}\cdot b_{2}\cdot \ldots \cdot b_{n}){\pmod {m}}.}

При этом нельзя выполнять эти операции со сравнениями, если их модули не совпадают.

К обеим частям сравнения можно прибавить одно и то же число c{\displaystyle c}:

(a+c)≡(b+c)(modm).{\displaystyle (a+c)\equiv (b+c){\pmod {m}}.}

Также можно перенести число из одной части сравнения в другую со сменой знака:

a≡(b+c)(modm);{\displaystyle a\equiv (b+c){\pmod {m}};}

(a−c)≡b(modm).{\displaystyle (a-c)\equiv b{\pmod {m}}.}

Если числа a{\displaystyle a} и b{\displaystyle b} сравнимы по модулю m{\displaystyle m}, то их степени ak{\displaystyle a^{k}} и bk{\displaystyle b^{k}} тоже сравнимы по модулю m{\displaystyle m} при любом натуральном k{\displaystyle k}:

ak≡bk(modm).{\displaystyle a^{k}\equiv b^{k}{\pmod {m}}.}

K любой из частей сравнения можно прибавить целое число, кратное модулю, то есть, если числа a{\displaystyle a} и b{\displaystyle b} сравнимы по модулю некоторого числа m{\displaystyle m}, то и a+t1{\displaystyle a+t_{1}} сравнимо с b+t2{\displaystyle b+t_{2}} по модулю m{\displaystyle m}, где t1{\displaystyle t_{1}} и t2{\displaystyle t_{2}} — произвольные целые числа, кратные m{\displaystyle m}:

(a+t1)≡(b+t2)(modm).{\displaystyle (a+t_{1})\equiv (b+t_{2}){\pmod {m}}.}

Также обе части сравнения и модуль можно умножить на одно и то же число, то есть, если числа a{\displaystyle a} и b{\displaystyle b} сравнимы по модулю некоторого целого числа m{\displaystyle m}, то и числа aq{\displaystyle aq} и bq{\displaystyle bq} сравнимы по модулю числа mq{\displaystyle mq}, где q{\displaystyle q} — целое:

aq≡bq(modmq).{\displaystyle aq\equiv bq{\pmod {mq}}.}

Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: 14≡20(mod6){\displaystyle 14\equiv 20{\pmod {6}}}, однако, сократив в 2 раза, мы получаем ошибочное сравнение: 7≡10(mod6){\displaystyle 7\equiv 10{\pmod {6}}}. Правила сокращения для сравнений следующие.

Можно делить обе части сравнения на число, но только взаимно простое с модулем: если

ad≡bd(modm){\displaystyle {ad}\equiv {bd}{\pmod {m}}} и НОД(d,m)=1,{\displaystyle {(d,m)=1},} то

a≡b(modm){\displaystyle a\equiv b{\pmod {m}}}.

Если, число d{\displaystyle d} не взаимно просто с модулем, как было в примере, указанном выше, то сокращать на d{\displaystyle d} нельзя.

Можно одновременно разделить обе части сравнения и модуль на их общий делитель:

если ac≡bc(modmc){\displaystyle {ac}\equiv {bc}{\pmod {mc}}}, то a≡b(modm){\displaystyle a\equiv b{\pmod {m}}}.

Пример

Применение сравнений позволяет легко получать разнообразные признаки делимости. Например, выведем признак делимости натурального числа N на 7. Запишем N{\displaystyle N} в виде 10a+b{\displaystyle 10a+b} (то есть отделим цифру единиц). Условие, что N{\displaystyle N} делится нацело на 7, можно записать в виде: 10a+b≡(mod7).{\displaystyle 10a+b\equiv 0{\pmod {7}}.} Умножим это сравнение на −2{\displaystyle -2:}

−20a−2b≡(mod7).{\displaystyle -20a-2b\equiv 0{\pmod {7}}.}

Или, прибавив слева число 21a,{\displaystyle 21a,} кратное модулю:

a−2b≡(mod7).{\displaystyle a-2b\equiv 0{\pmod {7}}.}

Отсюда вытекает следующий признак делимости на 7: надо вычесть из числа десятков удвоенное число единиц, затем повторять эту операцию до тех пор, пока не получится двузначное или однозначное число; если оно делится на 7, то и исходное число делится. Например, пусть N=22624.{\displaystyle N=22624.} Алгоритм проверки:

N1=2262−2⋅4=2254; N2=225−2⋅4=217;N3=21−2⋅7=7{\displaystyle N_{1}=2262-2\cdot 4=2254;\ N_{2}=225-2\cdot 4=217;N_{3}=21-2\cdot 7=7}

Вывод: 22624 делится на 7.

Основные свойства пропорций

• Обращение пропорции. Если  ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то  ba=dc{\displaystyle \ {\frac {b}{a}}={\frac {d}{c}}}
• Перемножение крайних членов пропорции со средними (крест-накрест). Если  ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то  ad=bc{\displaystyle \ ad=bc}
• Перестановка средних и крайних членов. Если  ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то

 ac=bd{\displaystyle \ {\frac {a}{c}}={\frac {b}{d}}}    (перестановка средних членов пропорции),

 db=ca{\displaystyle \ {\frac {d}{b}}={\frac {c}{a}}}    (перестановка крайних членов пропорции).

Увеличение и уменьшение пропорции. Если  ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то

 a+bb=c+dd{\displaystyle \ {\dfrac {a+b}{b}}={\dfrac {c+d}{d}}}    (увеличение пропорции),

 a−bb=c−dd{\displaystyle \ {\dfrac {a-b}{b}}={\dfrac {c-d}{d}}}    (уменьшение пропорции).

Составление пропорции сложением и вычитанием. Если  ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то

 a+cb+d=ab=cd{\displaystyle \ {\dfrac {a+c}{b+d}}={\frac {a}{b}}={\frac {c}{d}}}    (составление пропорции сложением),

 a−cb−d=ab=cd{\displaystyle \ {\dfrac {a-c}{b-d}}={\frac {a}{b}}={\frac {c}{d}}}    (составление пропорции вычитанием).

Доказательство (составление пропорции сложением и вычитанием)

Докажем для сложения. Выразим c{\displaystyle c} через остальные члены пропорции: c=adb{\displaystyle c={\frac {ad}{b}}}. Тогда:

a+cb+d=a+adbb+d=(ab+ad)bb+d=a(b+d)b(b+d)=ab.{\displaystyle {\frac {a+c}{b+d}}={\frac {a+ad/b}{b+d}}={\frac {(ab+ad)/b}{b+d}}={\frac {a(b+d)}{b(b+d)}}={\frac {a}{b}}.}

Для вычитания доказательство аналогично. ■

Вычисление тройного интеграла путём уменьшения кратности

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов
меньшей кратности.

Рассмотрим трёхмерную область . Снизу и сверху (то есть по высоте)
эта область ограничена поверхностями и
.
С боковых сторон (то есть по ширине) область ограничена поверхностями и
. И, наконец,
по глубине (если Вы смотрите на область в направлении оси Ox) — поверхностями
и

Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область
была правильной. Она правильна тогда, когда прямая, параллельная оси
Oz, пересекает границу области не более чем в двух точках. Правильными
трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже —
прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.

Чтобы наглядно представить отличие правильности от
неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На
рисунке ниже — пример неправильной области — однополостный гиперболоид,
поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.

Мы будем рассматривать только правильные области.

Итак, область — правильная. Тогда для любой функции
, непрерывной в области
, справедлива формула

Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению
внутреннего определённого интеграла по переменной z (при постоянных x и y) и
внешнего двойного интеграла по двумерной области .

Переходя от двойного интеграла к повторному,
получаем следующую формулу для вычисления тройного интеграла:

Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три
определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому
внешнему (по переменной x). Для удобства восприятия последовательности вычислений три
«вложенных» интеграла можно записать так:

.

Из этой записи уже однозначно видно, что:

• сначала нужно интегрировать функцию
  по переменной z, а в качестве пределов интегрирования взять уравнения и

  поверхностей ограничивающих область снизу и сверху;

• получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов
  интегрирования взять уравнения и
  поверхностей,
  ограничивающих область с боковых сторон;
• получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов
  интегрирования взять уравнения и
  поверхностей, ограничивающих область по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

—

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:

.

Вычислим второй интеграл — по переменной y:

.

Теперь вычисляем самый внешний интеграл — по переменной x:

.

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

,

где — параллелепипед, ограниченный плоскостями
, ,
, ,
, .

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы
уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:

.

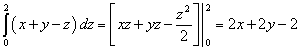Вычисляем интеграл «в серединке» — по переменной y. Получаем;

.

Теперь вычисляем самый внешний интеграл — по переменной x:

Ответ: данный тройной интеграл равен -2.

Пример 3. Вычислить тройной интеграл

,

где — пирамида, ограниченная плоскостью

и координатными плоскостями
, ,
. Область
проецируется на плоскость xOy в треугольник , как показано
на рисунке ниже.

Решение.
Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел
интегрирования задан однозначно: . Чтобы получить верхний
предел, выразим z из .
Получаем . Для интеграла
по переменной y нижний предел интегрирования задан однозначно: .
Для получения верхнего предела выразим y из ,
считая при этом, что (так как линия расположена в плоскости xOy).
Получаем: .

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:

.

Вычисляем средний интеграл — по переменной y. Получаем:

Наконец, вычисляем самый внешний интеграл — по переменной x:

Ответ: данный тройной интеграл равен 1/8.

Решение

AFAIK, традиционным обозначением отрицания было , однако оно было неудобным в двух основных ситуациях:

1. Когда текст содержит большое количество вложенных отрицаний, текст пересыщается скобочками и становится непонятным. В этом случае удобно использовать надчёркивание, потому что это визуально понятно и не требует скобочек. Дело вкуса: мне, например, не лень обрамлять отрицание скобочками, зато каждую импликацию с двух сторон выделять — явно перебор.

2. Когда текст набирается на компьютере/печатной машинке. В этом случае проще использовать те символы, которые есть на клавиатуре, а именно !, — и

. По этой же причине вместо пишут && и || или словами (к слову, &≡et). Как и любую другую основанную на лени практику, я расцениваю её отрицательно. Впрочем, некогда из подобной практики возникла -нотация.

Законы алгебры логики

Исключение констант	\( 1 + A = 1 \)\( 0 ⋅ A = 0 \)\( 0 + A = A \)\( 1 ⋅ A = A \)
Идемпотентность	\( A + A = A \)\( A ⋅ A = A \)
Закон исключения третьего	\( A + \overline{A} = 1 \)
Закон непротиворечивости	\( A ⋅ \overline{A} = 0 \)
Закон отрицания	\( \overline{\overline{A}} = A \)
Закон коммутативности	\( A + B = B + A \)\( A ⋅ B = B ⋅ A \)
Закон ассоциативности	\( A + B + C = A + (B + C)\)\( A ⋅ B ⋅ C = A ⋅ (B ⋅ C)\)
Закон дистрибутивности	\( A ⋅ (B + C) = A ⋅ B + A ⋅ C \)\( A + (B ⋅ C) = (A + B) ⋅ (A + C) \)
Правило де Моргана	\( \overline{(A + B)} = \overline{A} ⋅ \overline{B}\)\( \overline{(A ⋅ B)} = \overline{A} + \overline{B}\)
Закон поглощения	\( A + A ⋅ B = A\)\( A ⋅ (A + B) = A\)
Закон склеивания	\( A ⋅ B + \overline{A} ⋅ B = B \)\( (A + B) ⋅ (\overline{A} + B) = B \)

Законы алгебры можно доказать составив таблицу истинности.

Умножитель на базе индексного метода

Однако существует метод, который требует одной (или для удобства двух) таблиц размерности . Метод основан на замене умножения сложением. И может быть схематично проиллюстрирован следующим рисунком (рис. 2):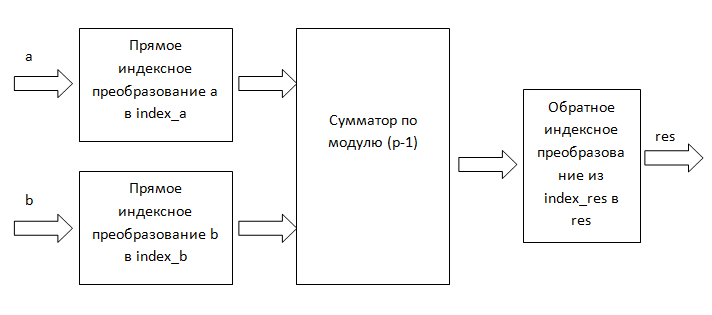Рисунок 2. Индексное умножение.

Поясним, почему это возможно. Индексное представление числа основывается на понятии первообразного корня по простому модулю . Первообразным корнем w является целое число, возведение которого в степень дает неповторяющиеся вычеты по модулю . Первообразный корень всегда существует для любого простого (доказано Гауссом в 1801 году). В этом случае каждому целому числу из промежутка можно поставить в соответствие число такое что: i. И таким образом получить следующее соответствие: .

Рассмотрим пример для модуля . Первообразный корень для этого значения модуля равен 2. Как несложно убедиться возведение в степень 0, 1, … 9 дает неповторяющиеся результаты:

• (2) 11 = 1 11 = 1
• (21) 11 = 2 11 = 2
• (22) 11 = 4 11 = 4
• (23) 11 = 8 11 = 8
• (24) 11 = 16 11 = 5
• (25) 11 = 32 11 = 10
• (26) 11 = 64 11 = 9
• (27) 11 = 128 11 = 7
• (28) 11 = 256 11 = 3
• (29) 11 = 512 11 = 6

Для получения таблицы преобразования между обычным и индексным представлением необходимо отсортировать полученные пары значений в порядке возрастания. Таким образом, таблица прямого преобразования для модуля = 11 будет выглядеть следующим образом:

q	1	2	3	4	5	6	7	8	9	10
i	1	8	2	4	9	7	3	6	5

А таблица обратного преобразования для модуля = 11 будет выглядеть так:

i	1	2	3	4	5	6	7	8	9
q	1	2	4	8	5	10	9	7	3	6

Найдем значение выражения (3*5) 11. Числа 3 и 5 имеют соответствующие индексы 8 и 4 (см. таблицу 1). Просуммировав эти индексы по модулю (11-1) = 10 получим результат (8+4) 10 = 12 10 = 2. Из таблицы 2 находим, что обратное преобразование для индекса 2 дает конечный результат, равный 4.

Структурную схему индексного умножителя по модулю m=11 для рассмотренного примера можно посмотреть на следующем рисунке (рис 3):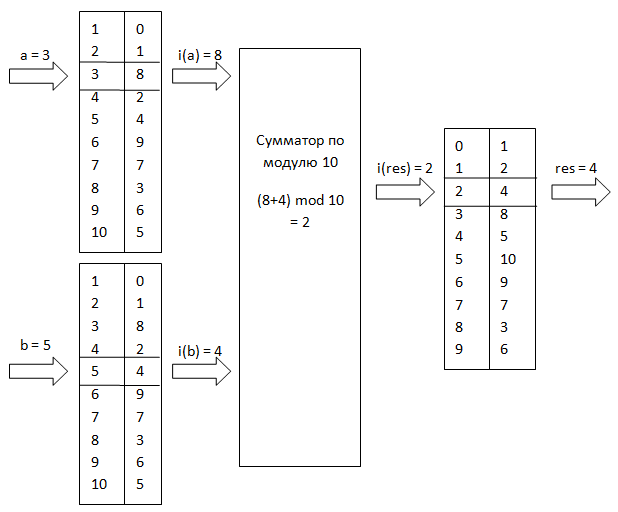Рисунок 3. Схема индексного умножителя для p = 11.

2.1Высказывания

Примеры высказываний

Как бы определение 1. Высказывание — это утверждение с чётко определенным смыслом, которое может
быть истинным или ложным.

Как обычно, проще привести несколько примеров.

Пример.

• «2+2=5» — пример высказывания. Оно ложно.
• «3>2» — ещё один пример высказывания. Оно истинно.
• «5 — простое число» — ещё одно истинное высказывание.
• «Множество простых чисел конечно» — это ложное высказывание.
• «Если целое число простое и оно больше двух, оно нечётно» —
  истинное высказывание.
• «Каждое чётное число, большее двух, можно представить в виде суммы
  двух простых чисел» — это высказывание, истинность которого в
  настоящий момент неизвестна (это так называемая бинарная проблема
  Гольдбаха).
• «n — чётное число» — это не высказывание, потому что непонятно,
  чему равно n (здесь, конечно, под n подразумевается не
  собственно буква, а переменная, которая может принимать разные
  значения), и поэтому это утверждение не является ни ложным, ни
  истинным. С такого типа утверждениями (они называются предикатами)
  мы познакомимся чуть позже.

Вместо «истинно» или «ложно» используются и другие синонимичные выражения:
верно (неверно), корректно (некорректно) и т.д.

Операции с высказываниями

AB

Определение 1. Высказывание «верно по крайней мере одно из двух высказываний A или B (или
оба)», называется дизъюнкцией высказываний A и B. Оно
обозначается A∨B. Другой термин для дизъюнкции — логическое
«ИЛИ».

Определение 2. Высказывание «верны оба высказывания A и B» называется
конъюнкцией высказываний A и B. Оно обозначается A∧B.
Другой термин для конъюнкции — логическое «И».

Определение 3. Высказывание «высказывание A неверно» называется отрицанием A.
Обозначается ¬A. Другой термин — логическое «НЕ».

Если про каждое из высказываний A и B известно, является оно истинным или
ложным, легко установить истинность их конъюнкции, дизъюнкции и отрицания.
Например, если A истинно, то ¬A ложно. Если A и B оба истинны, то
A∧B истинно, иначе оно ложно. И так далее. Эту информацию удобно
записывать в виде табличек, которые называются таблицами истинности.

Таблица истинности для отрицания выглядит так:

A¬AИЛЛИ

ABA∨BA∧BИИИИИЛИЛЛИИЛЛЛЛЛ

Раскрытие скобок с отрицанием

AB¬(A∨B)AB
¬(A∨B)=(¬A)∧(¬B)

¬(A∧B)AB
¬(A∧B)=(¬A)∨(¬B)

∨∧

Эти правила преобразования формул в алгебре логики называются законами де
Моргана.

Замечание 1. Законы де Моргана мгновенно обобщаются на случай большего количества
высказываний. Например, ¬(A∧B∧C)=(¬A)∨(¬B)∨(¬C).

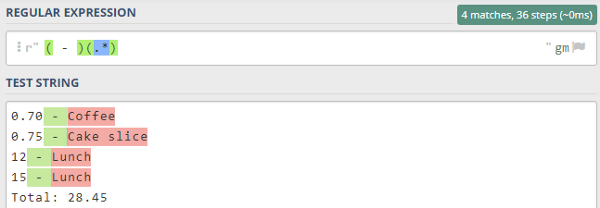
Скобочные группы ― ()

a(bc)       создаём группу со значением bc -> тестa(?:bc)*    оперетор ?: отключает группу -> тестa(?<foo>bc) так, мы можем присвоить имя группе -> тест

Этот оператор очень полезен, когда нужно извлечь информацию из строк или данных, используя ваш любимый язык программирования. Любые множественные совпадения, по нескольким группам, будут представлены в виде классического массива: доступ к их значениям можно получить с помощью индекса из результатов сопоставления.

Если присвоить группам имена (используя ), то можно получить их значения, используя результат сопоставления, как словарь, где ключами будут имена каждой группы.

Кратко о законе отрицания отрицания

Сформулируем теперь определение отрицания. Отрицание — это процесс, который, сохраняя сущность существующего, отменяет форму и существование того, что было. Сформулировав это абстрактное определение отрицания, мы должны углубить наше понимание, изучив конкретные или практические примеры. Философия — наука сложная. Третий закон диалектики, который подразумевает отрицание отрицания, выражает понятие развития.

Вместо замкнутого круга, где процессы постоянно повторяются, этот закон указывает на то, что движение через последовательные противоречия фактически приводит к развитию, от простого к сложному, от низшего к высшему. Процессы не идентичны, несмотря на то что создается впечатление, словно они одинаковы. Отрицание отрицания вовсе не предполагает возврата к первоначальной идее, а скорее, имеет в виду повторение ранних форм на качественно более высоком уровне.

Вставка символов с помощью комбинации клавиш

Способ пригодится, если нужные символы будут встречаться в документе часто. Чтобы каждый раз не тратить время на ввод знака через меню «Символы», проще запомнить или записать в ежедневнике сочетание клавиш для нужных символов.

Заходим в раздел «Символы», в качестве примера возьмем знак «Бесконечность». Находим код выбранного знака 221E и сочетание клавиш Alt+X.

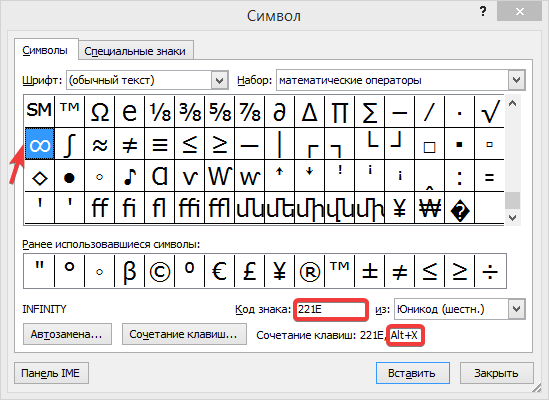
Это означает, что добавить в документ знак бесконечности можно так: установить курсор в нужном месте, набрать код символа и комбинацию Alt+X.

Аналогично поступаем с другими знаками. Например, нам требуется обозначение математического корня в лабораторной работе. найдем его в таблице. Код символа 221A, комбинация клавиш для исполнения команды Alt+X.

Метод введения символов с помощью сочетания клавиш требует использовать цифровую клавиатуру Num Lock. Перед работой убедитесь, что она включена.

Работать с дополнительными символами не сложно. Тем, кто регулярно вводит их в документ, проще освоить второй способ — ввод через комбинацию клавиш. На первых порах процесскажется хлопотным, но запомнив частые комбинации, вы будете делать это на автоматиз ме и существенно облегчите себе работу.

2.2Предикаты и кванторы

Примеры предикатов

nnпредикатами

Как бы определение 2. Грубо говоря, предикат — это такое утверждение, которое зависит от
одной или нескольких переменных, и становится высказыванием, если задать
значения этих переменных.

Пример 1. Рассмотрим предикат «n — чётное число». Его можно обозначить
какой-нибудь буквой, аналогично обозначению функций — например,
E(n). При подстановке конкретного n предикат становится
высказыванием, которое является истинным или ложным. Например,
E(2) истинно, а E(17) — ложно. Подобно функциям, у
предикатов есть «область определения» — множество значений, которые
могут принимать переменные. Например, давайте считать, что областью
определения для E(n) является множество натуральных чисел, n∈N (но можно было бы определить аналогичный предикат и для множества
всех целых чисел).

Пример 2. Определим предикат D(k,n) — «n делится на k». Этот
предикат зависит от двух переменных. Будем считать, что n∈N и k∈N. Например, D(2,3) — ложь, а D(2,4) — истина.

Пример 3. Ещё нам понадобится предикат S(x,y)=x2=y, определенный для
вещественных x и y. Он провреяет, что x2 равняется y.

Одни предикаты можно определять через другие. Например, если бы у нас был
готовый предикат D, проверяющий делимость, и нам нужно было изготовить из него
предикат E, проверяющий число на чётность, его легко можно было бы задать
таким образом:

E(n)=D(2,n).

Квантор всеобщности

T(n)=D(1,n)n1nT(n)
∀nT(n).

∀allквантором
всеобщности
∀n∈NT(n).

Вопрос 1. Рассмотрим утверждение ∀n∈NE(n), где E(n) —
предикат, проверяющий, что n чётное число. Что вы можете сказать про
построенное таким образом утверждение?

  Оно истинно.

Вы уверены? В этом утверждении сказано: «для любого натурального
n верно, что n чётно». Иными словами, это утверждение можно
переписать так: «все натуральные числа — чётны».

  Оно ложно.

Да, потому что бывают нечётные числа. Например, E(3) — ложно.

  Невозможно определить его истинность, зависит от значения n.

Нет! В этом утверждении сказано: «для любого натурального n
верно, что n чётно». Иными словами, это утверждение можно
переписать так: «все натуральные числа — чётны». Это утверждение
попросту неверно.

Пусть P(x) — какой-то предикат. Рассмотрим утверждение ∀xP(x). Если P(x) при всех значениях x является истинным, значит, это
утверждение истинно. В противном случае, ложно. Поэтому получившееся
утверждение не является предикатом, оно является просто высказыванием,
которое может быть истинным или ложным. Заметим, что хотя переменная x
фигурирует в этом утверждении, мы не можем подставлять вместо неё какие-либо
конкретные значения. Нельзя записать ∀2P(2), это не имеет
смысла, поскольку после квантора обязательно должна идти переменная, а не
какое-то конкретное число. Переменная x в этом случае называется
связанной: она существует как бы только внутри утверждения, но
«извне» мы не можем её менять.

Квантор существования

Совершенными числами

Рассмотрим предикат R(n), проверяющий, является ли натуральное число n
совершенным. (Иными словами, R(n) соответствует утверждению «n совершенное
число».)

Если взять какое-то конкретное n, очень легко проверить, является ли оно
совершенным. Например, число 10 имеет три собственных делителя, 5, 2 и
1, но 5+2+1=8≠10 — значит, оно не совершенное. Но существуют ли вообще
совершенные числа? Иными словами, верно ли утверждение: «существует такое n,
что R(n) имеет значение „истина”»?

Для формулирования таких утверждений также есть специальное короткое
обозначение:

∃nR(n)

∃n∈NR(n).

∃existsквантором существования

Аналогично квантору всеобщности (см. ), квантор
существования «связывает» соответствующую переменную. Утверждение ∃nR(n), хотя в нём фигурирует переменная n, не является предикатом,
зависящим от n. Это просто высказывание, которое является истинным (если
совершенные числа существуют), или ложным (если их нет).

Кстати, совершенные числа существуют. Например, число 6 совершенно. Это
доказывает, что утверждение ∃nR(n) является истинным.

Кванторы и отрицание

P(x)xP(x)x

Рассмотрим высказывание ∀xP(x) («все крокодилы красные»). Чтобы
его опровергнуть (то есть доказать его отрицание), достаточно предъявить
какого-нибудь крокодила, который бы не был красным. Иными словами, верно
равенство:

¬(∀xP(x))=(∃x¬P(x))(2.1)

∃xP(x)
¬(∃xP(x))=(∀x¬P(x))(2.2)

Замечание 3. Рассмотрим какой-нибудь предикат P(x), определенный на множестве {1,2,3}. Тогда утверждение ∀xP(x) эквивалентно такому: P(1)∧P(2)∧P(3). Его отрицание легко переписать по законам де
Моргана: ¬(P(1)∧P(2)∧P(3))=(¬P(1))∨(¬P(2))∨(¬P(3)). Которое в свою очередь эквивалентно ∃x¬P(x).

Равенство и неравенство

Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.

Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн формате. Как найти знаки на клавиатуре? Ответ на картинке:

Источник статьи: http://skysmart.ru/articles/mathematic/znaki-bolshe-menshe-ili-ravno

Тройной интеграл в сферических координатах

Если область интегрирования в тройном интеграле представляет собой шар или часть шара,
то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M
характеризуют три величины (ρ, φ, θ), где ρ — расстояние от точки
M до начала координат , φ — угол между вектором ON и положительным
направлением оси Ox (N — проекция точки M на плоскость xOy),
θ — угол между вектором OM и положительным направлением оси Oz.

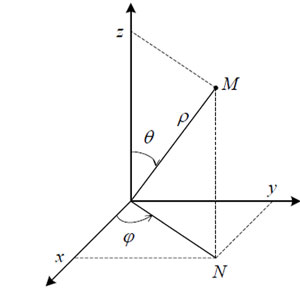
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями

,

,

.

Элемент объёма в сферических координатах выражается следующим образом:

.

Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к
сферическим координатам осуществляется по формуле:

Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же,
как при вычислениях в прямоугольных декартовых и цилиндрических координатах — перейти к повторным
интегралам (последовательности трёх определённых интегралов):

Пример 9. Вычислить тройной интеграл

переходом к сферическим координатам, где —
область, ограниченная неравенствами и
.

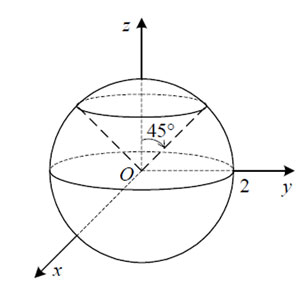
Решение. Снизу область интегрирования ограничена конической поверхностью
, а сверху — сферой
. Так как область
интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную
функцию:

Учитывая, что ,
получаем

Расставим пределы интегрирования и перепишем последний полученный интеграл в виде
трёх повторных интегралов. По рисунку видно, что
,
,
. Поэтому

Итак, тройной интеграл вычислен. Так как все три интеграла — независисмые друг от друга,
мы смогли интегрировать каждый отдельно и результаты перемножить.

Связь с естественным языком

В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:

1. «результат истинен (равен 1), если A не равно B (A≠B)»;
2. «если A не равно B (A≠B), то истина (1)».

Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}.

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

1. A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
2. A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).

Операция ⊕{\displaystyle \oplus }исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ».
Операция ∨{\displaystyle \lor }включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ».
Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

Где искать символы?

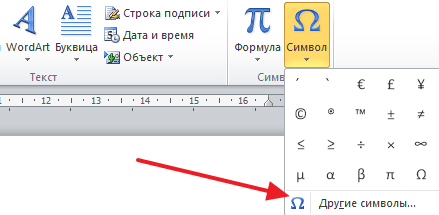
Чтобы в Word открылась панель специальных символов, запустите программу, кликните «Вставка», перейдите к блоку «Символ». Откроется панель со специальными знаками, которые, по мнению разработчиков, чаще всего пользуются спросом.

Если нужные символы отсутствуют, кликните «Другие символы». Откроются все доступные знаки.

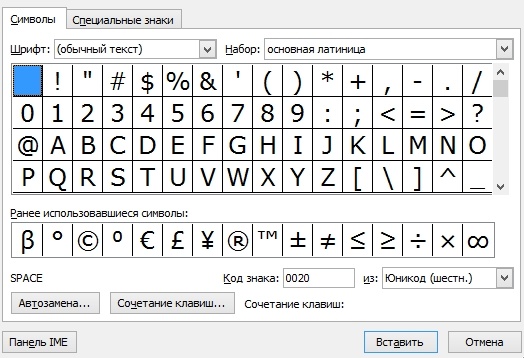
В открывшемся окне мы увидим много разных символов, сгруппированных по назначению и стилю. Чтобы не путаться и быстро отыскать нужный знак, найдите дополнительный параметр поиска в разделе «Набор». Помимо основной латиницы, можно выбрать математические или фонетические знаки, денежные единицы, геометрические фигуры и др.

Логические выражения

Определение

Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».

Их можно разделить на два типа:

• выражения, использующие операции сравнения и принимающие логические значения. Например, выражение a < b, где a = 12, а b = 9, равно значению «ложь»;
• логические выражения, которые связаны с логическими величинами и операциями. Например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина.

В логические выражения могут входить функции, алгебраические операции, операции сравнения и логические операции. Для таких случаев существует алгоритм выполнения действий. За исключением тех случаев, когда в логическом выражении присутствуют скобки, влияющие на порядок выполнения операций.

• вычисляется существующие функциональные зависимости;
• вычисляются алгебраические операции в обычном порядке;
• вычисляются операции сравнения в любом порядке;
• вычисляются логические операции начиная с операции отрицания. Следом вычисляется операция логического умножения, логического сложения, в последнюю очередь выполняются операции импликации и эквивалентности.

История

Первое известное определение равных пропорций было дано как равенство последовательных вычитаний, современным языком это можно выразить как равенство цепных дробей для отношений величин.
Позже Евдокс Книдский упростил определение, равенство пропорций ab=cd{\displaystyle a:b=c:d} им определялось как одновременное выполнение одной из трёх пар соотношений

• m⋅a>n⋅b{\displaystyle m\cdot a>n\cdot b} и m⋅c>n⋅d{\displaystyle m\cdot c>n\cdot d},
• m⋅a=n⋅b{\displaystyle m\cdot a=n\cdot b} и m⋅c=n⋅d{\displaystyle m\cdot c=n\cdot d},
• m⋅a<n⋅b{\displaystyle m\cdot a<n\cdot b} и m⋅c<n⋅d{\displaystyle m\cdot c<n\cdot d}

для любой пары натуральных чисел m{\displaystyle m} и n{\displaystyle n}.
Это определение даётся в «Началах» Евклида.

С появлением вещественных чисел отпала необходимость в специальной теории пропорций, древние математики не рассматривали пропорции длины как числа.
Определение Евдокса, данное в несколько более абстрактном виде, использовалось далее при определении вещественных чисел Дедекиндом через сечения.

Риска над буквой (Макрон) в Microsoft Office Word

Как поставить над буквой риску? Вроде мелочи, но не каждый знает, как это сделать. Где используется такая риска? Например, в химических или математических формулах. Рассмотрим, как поставить значок электрона, например 4е̄.

Примеры показаны на Microsoft Office 2016, но должны также работать и на других версиях.

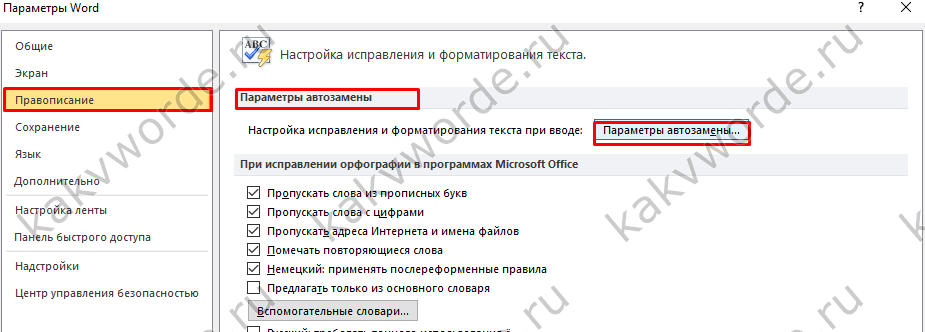
Первый способ — более длинный. Переходим в «Вставка → Уравнение». Появится область под названием «Место для уравнения». Если область не активна — щелкните на нее левой клавишей мыши. Должен открыться «Конструктор» с различными формулами.

Нам нужны «Диакритические знаки» (см. скриншот ниже)

Выбираем знак с риской, нажав на него. Остается на место пустого символа написать нужную букву или цифру — в нашем случае букву е.

Второй способ. Ставим курсор после символа, над которым нужно написать данный знак. Идем в «Вставка → Символ → Другие символы → объединенные диакр. знаки» и ищем нужный знак. Можно значительно быстрее: напротив «Код знака» вводим цифры 0304 (чтобы быстро найти нужный) и нажимаем «Вставить».

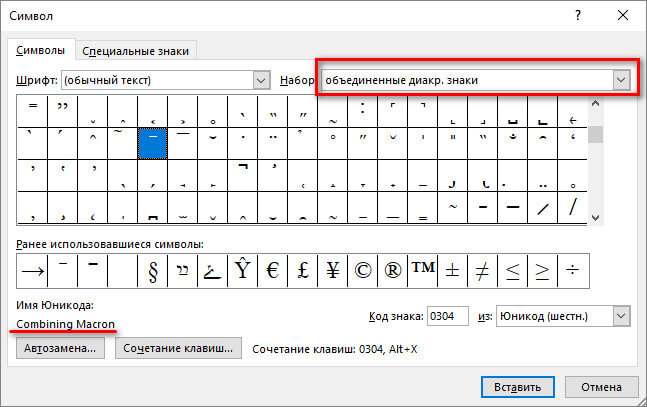
Если вы часто пользуетесь данным знаком, то можно настроить сочетание «горячих» клавиш для быстрой вставки. Для этого нажимаем «Сочетание клавиш» и в поле «Новое сочетание клавиш» пишем, например, ctrl + m, тогда нажимаем «Назначить», а потом «Закрыть». Теперь при нажатии клавиши ctrl и не отпуская ее m будет вставлен символ.

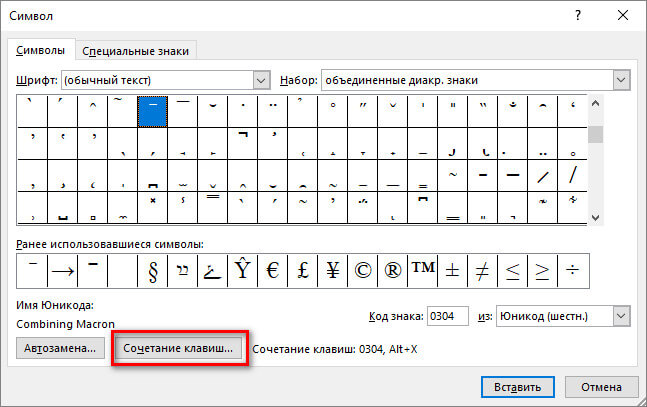
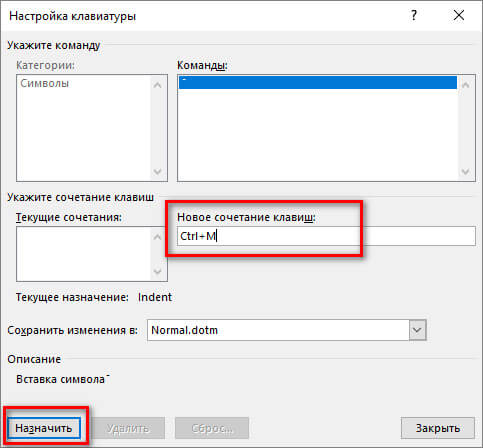
Третий способ. Последний способ самый быстрый. Для этого пишем нужную букву, ставим курсор за ней, и держа клавишу alt на дополнительной цифровой клавиатуре (клавиша num lock должна быть включена) набираем 772. Готово. Если набрать вместо 772 — 773, то риска будет немного выходить за символ.

Как отформатировать диск в Ubuntu