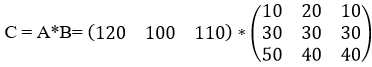Матрицы. основы
Содержание:
- 7.3. Статистика
- Создание векторов и матриц
- Обработка изображений в NumPy
- 1.2. Заполнение данными
- Транспонирование
- 3.10. Прочие математические функции
- Основные логические функции, используемые в Эксель
- 1.1. Автозаполнение массивов
- Арифметические операции над массивами NumPy
- 3.8. Арифметические операции
- Копии и представления
- Другие решения
- Двумерные массивы
- Создание матрицы
- Заполнение матрицы произвольными значениями
- Вывод матрицы на экран
- Сортировка, поиск, подсчет¶
- 7.1.1. Значения -inf, inf и nan
- 3.4. Суммы, разности, произведения
- Произведение матриц
- Дискретное преобразование Фурье (numpy.fft)¶
- Создание, вывод и ввод матрицы в Питоне
7.3. Статистика
Над данными в массивах можно производить определенные вычисления, однако, не менее часто требуется эти данные как-то анализировать. Зачастую, в этом случае мы обращаемся к статистике, некоторые функции которой тоже имеются в NumPy. Данные функции могут применять как ко всем элементам массива, так и к элементам, расположенным вдоль определенной оси.
Элементарные статистические функции:
Средние значения элементов массива и их отклонения:
Корреляционные коэфициенты и ковариационные матрицы величин:
Так же NumPy предоставляет функции для вычисления гистограмм наборов данных различной размерности и некоторые другие статистичские функции.
Создание векторов и матриц
Вектора и матрицы – это основные объекты, которыми приходится оперировать в машинном обучении. Numpy предоставляет довольно много удобных функций, которые строят эти объекты.
Перед тем как их использовать не забудьте импортировать Numpy в проект.
>>>import numpy as np
np.arange()
Функция arange() аналогична по своему назначению функции range() из стандартной библиотеки Python. Ее основное отличие заключается в том, что arange() позволяет строить вектор с указанием шага в виде десятичной дроби.
Синтаксис использования функции следующий:
arange(stop)
arange(start, stop)
arange(start, stop, step)
В первом варианте будет создан вектор из целых чисел от 0 до stop.
>>> np.arange(10) array()
Второй вариант позволяет задавать интервал, в этом случае вектор также будет содержать целые числа.
>>> np.arange(5, 12) array()
Третий вариант позволяет определить интервал чисел и шаг, который может быть десятичным числом
>>> np.arange(1, 5, 0.5) array()
np.matrix()
Matrix является удобным инструментом для задания матрицы. При этом можно использовать Matlab стиль, либо передать в качестве аргумента список Python (или массив Numpy).
Вариант со списком Python.
>>> a = , ] >>> np.matrix(a) matrix(, ])
Вариант с массивом Numpy.
>>> b = np.array(, ]) >>> np.matrix(b) matrix(, ])
Вариант в Matlab стиле.
>>> np.matrix('')
matrix(,
])
np.zeros(), np.eye()
В арсенале Numpy есть функции для создания специальных матриц: нулевых и единичных. Нулевой называется матрица, состоящая полностью из нулей. Для ее создания удобно использовать функцию zeros(), в качестве аргумента в нее передается кортеж из двух элементов, первый из них – это количество строк, второй – столбцов.
>>> np.zeros((3, 4)) array(, , ])
Функция eye() создает единичную матрицу – квадратную матрицу, у которой элементы главной диагонали равны единицы, все остальные – нулю.
>>> np.eye(3) array(, , ])
Обработка изображений в NumPy
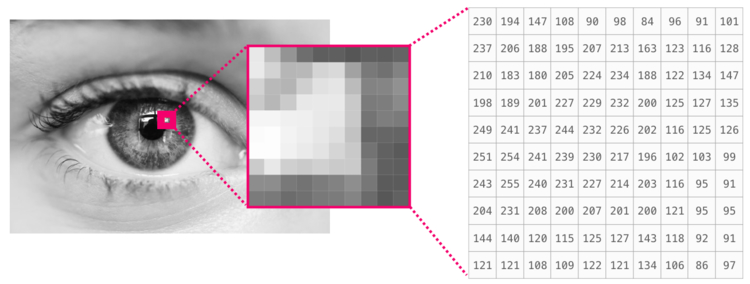
Изображение является матрицей пикселей по размеру (высота х ширина).
Если изображение черно-белое, то есть представленное в полутонах, каждый пиксель может быть представлен как единственное число. Обычно между 0 (черный) и 255 (белый). Хотите обрезать квадрат размером пикселей в верхнем левом углу картинки? Просто попросите в NumPy .
Вот как выглядит фрагмент изображения:
Если изображение цветное, каждый пиксель представлен тремя числами. Здесь за основу берется цветовая модель RGB — красный (R), зеленый (G) и синий (B).
В данном случае нам понадобится третья размерность, так как каждая клетка вмещает только одно число. Таким образом, цветная картинка будет представлена массивом с размерностями: (высота х ширина х 3).

1.2. Заполнение данными
- Создает массив NumPy.
- Преобразует последовательность в массив NumPy.
- Преобразует последовательность в массив NumPy, пропуская подклассы ndarray.
- Возвращает непрерывный массив в памяти с организацией порядка элементов в С-стиле.
- Интерпретирует входные данные как матрицу.
- Возвращает копию массива.
- Преобразует буфер в одномерный массив.
- Создает массив из текстового или двоичного файла.
- Создает массив с выполнением указанной функции над каждым элементом.
- Создает одномерный массив из итерируемого объекта.
- Создает одномерный массив из строки.
- Создает массив из данных в текстовом файле.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
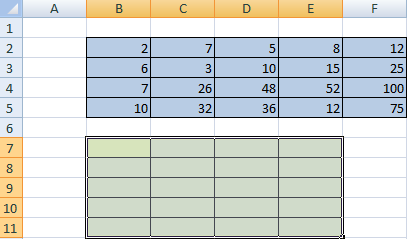
1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
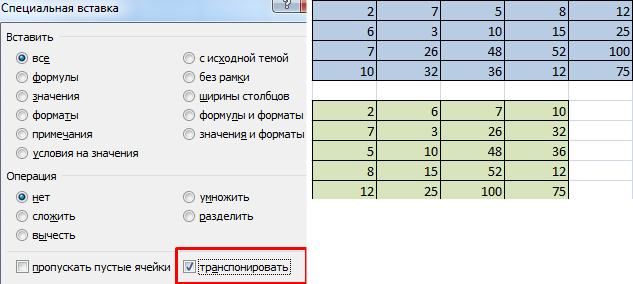
2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
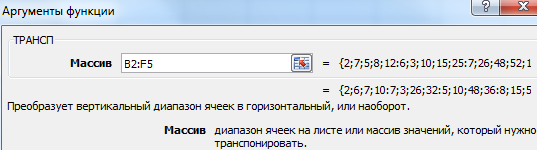
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
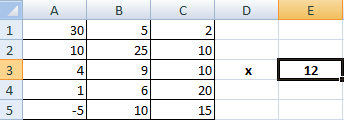
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
3.10. Прочие математические функции
- Дискретная линейная свертка.
- Ограничение значений массивов указанным интервалом допустимых значений.
- Квадратный корень элементов массива.
- Кубический корень элементов массива.
- Квадрат элементов массива.
- Абсолютное значение (модуль) элементов массива.
- Возвращает абсолютное значение (модуль) элементов массива в виде чисел с плавающей точкой.
- Элементарный указатель на знак числа.
- Ступенчатая функция Хевисайда.
- Наибольшие значения после поэлементного сравнения значений массивов.
- Наименьшие значения после поэлементного сравнения значений массивов.
- Наибольшие значения после поэлементного сравнения значений массивов в виде чисел с плавающей точкой.
- Наименьшие значения после поэлементного сравнения значений массивов в виде чисел с плавающей точкой.
- Заменяет nan на 0, бесконечность и минус-бесконечность заменяются на наибольшее и наименьшее доступное число с плавающей точкой соответственно.
- Переводит комплексные числа в вещественные если мнимая часть комплексного числа меньше машинной эпсилон.
- Одномерная линейная интерполяция.
Основные логические функции, используемые в Эксель
1.1. Автозаполнение массивов
- Возвращает новый массив заданной формы и типа без инициированных записей.
- Возвращает новый массив с формой и типом данных указанного массива без инициированных записей.
- Возвращает новый массив в котором диагональные элементы равны единице, а все остальные равны нулю.
- Возвращает новый квадратный массив с единицами по главной диагонали.
- Возвращает новый массив заданной формы и типа, заполненный единицами.
- Возвращает новый массив с формой и типом данных указанного массива, заполненный единицами.
- Возвращает новый массив заданной формы и типа, заполненный нулями.
- Возвращает новый массив с формой и типом данных указанного массива, заполненный нулями.
- Возвращает новый массив заданной формы и типа все элементы которого равны указанному значению.
- Возвращает новый массив с формой и типом данных указанного массива, все элементы которого равны указанному значению.
Арифметические операции над массивами NumPy
Создадим два массива NumPy и продемонстрируем выгоду их использования.
Массивы будут называться и :

При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать :

Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.
Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:

Довольно часто требуется выполнить какую-то арифметическую операцию между массивом и простым числом. Ее также можно назвать операцией между вектором и скалярной величиной. К примеру, предположим, в массиве указано расстояние в милях, и его нужно перевести в километры. Для этого нужно выполнить операцию :

Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.
3.8. Арифметические операции
- Поэлементно вычисляет наименьшее общее кратное массивов x1 и x2.
- Поэлементно вычисляет наибольший общий делитель массивов x1 и x2.
- Поэлементная сумма значений массивов.
- Вычисляет обратное значение () каждого элемента массива.
- Эквивалентно простому копированию () элементов массива, но только для массивов поддерживающих математические операции. Формально соответствует математической записи .
- Отрицательное значение элементов массива.
- Поэлементное умножение значений массива x1 на значения массива x2.
- Поэлементное деление значений массива x1 на значения массива x2.
- Поэлементное возведение значений массива x1 в степень равную значениям из массива x2.
- Поэлементная разность значений массива x1 и x2.
- Поэлементное истинное деление значений массива x1 на значения массива x2.
- Поэлементное целочисленное деление значений массива x1 на значения массива x2.
- Поэлементное возведение значений массива x1 в степень равную значениям из массива x2, адаптированное для чисел с плавающей точкой.
- Поэлементный остаток от деления значений массива x1 на значения массива x2.
- Поэлементно вычисляет остаток от деления значений массива x1 на значения массива x2.
- Дробная и целая часть элементов массива.
- Элементарный остаток от деления значений массива x1 на значения массива x2.
- Результат истинного деления и остаток от деления значений массива x1 на значения массива x2.
Копии и представления
При работе с массивами, их данные иногда необходимо копировать в другой массив, а иногда нет. Это часто является источником путаницы. Возможно 3 случая:
Вообще никаких копий
Простое присваивание не создает ни копии массива, ни копии его данных:
>>> a = np.arange(12) >>> b = a # Нового объекта создано не было >>> b is a # a и b это два имени для одного и того же объекта ndarray True >>> b.shape = (3,4) # изменит форму a >>> a.shape (3, 4)
Python передает изменяемые объекты как ссылки, поэтому вызовы функций также не создают копий.
Представление или поверхностная копия
Разные объекты массивов могут использовать одни и те же данные. Метод view() создает новый объект массива, являющийся представлением тех же данных.
>>> c = a.view()
>>> c is a
False
>>> c.base is a # c это представление данных, принадлежащих a
True
>>> c.flags.owndata
False
>>>
>>> c.shape = (2,6) # форма а не поменяется
>>> a.shape
(3, 4)
>>> c,4 = 1234 # данные а изменятся
>>> a
array(,
,
])
Срез массива это представление:
>>> s = a = 10
>>> a
array(,
,
])
Глубокая копия
Метод copy() создаст настоящую копию массива и его данных:
>>> d = a.copy() # создается новый объект массива с новыми данными
>>> d is a
False
>>> d.base is a # d не имеет ничего общего с а
False
>>> d, = 9999
>>> a
array(,
,
])
Другие решения
Это будет зависеть от вашего приложения, но в целом самый быстрый способ транспонировать матрицу — это инвертировать ваши координаты, когда вы просматриваете, тогда вам не нужно фактически перемещать какие-либо данные.
37
1
Рассматривайте каждую строку как столбец, а каждый столбец — как строку .. используйте j, i вместо i, j
1
транспонирование без каких-либо накладных расходов (класс не завершен):
можно использовать так:
конечно, я не беспокоился об управлении памятью здесь, что является важной, но другой темой. 1
1
Я думаю, что самый быстрый способ не должен брать больше, чем O (n ^ 2), и таким образом вы можете использовать только O (1) пробел:
способ сделать это — поменяться парами, потому что когда вы перемещаете матрицу, то вы делаете следующее: M = M , поэтому сохраняйте M в temp, тогда M = M , и последний шаг: M = темп. это может быть сделано за один проход, поэтому это должно занять O (n ^ 2)
-1
мой ответ транспонирован из матрицы 3х3
-5
Двумерные массивы
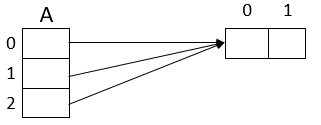
Выше везде элементами массива были числа. Но на самом деле элементами массива может быть что угодно, в том числе другие массивы. Пример:
a = b = c = z =
Что здесь происходит? Создаются три обычных массива , и , а потом создается массив , элементами которого являются как раз массивы , и .
Что теперь получается? Например, — это элемент №1 массива , т.е. . Но — это тоже массив, поэтому я могу написать — это то же самое, что , т.е. (не забывайте, что нумерация элементов массива идет с нуля). Аналогично, и т.д.
То же самое можно было записать проще:
z = , , ]
Получилось то, что называется двумерным массивом. Его можно себе еще представить в виде любой из этих двух табличек:
Первую табличку надо читать так: если у вас написано , то надо взять строку № и столбец №. Например, — это элемент на 1 строке и 2 столбце, т.е. -3. Вторую табличку надо читать так: если у вас написано , то надо взять столбец № и строку №. Например, — это элемент на 2 столбце и 1 строке, т.е. -3. Т.е. в первой табличке строка — это первый индекс массива, а столбец — второй индекс, а во второй табличке наоборот. (Обычно принято как раз обозначать первый индекс и — второй.)
Когда вы думаете про таблички, важно то, что питон на самом деле не знает ничего про строки и столбцы. Для питона есть только первый индекс и второй индекс, а уж строка это или столбец — вы решаете сами, питону все равно
Т.е. и — это разные вещи, и питон их понимает по-разному, а будет 1 номером строки или столбца — это ваше дело, питон ничего не знает про строки и столбцы. Вы можете как хотите это решить, т.е. можете пользоваться первой картинкой, а можете и второй — но главное не запутайтесь и в каждой конкретной программе делайте всегда всё согласованно. А можете и вообще не думать про строки и столбцы, а просто думайте про первый и второй индекс.
Обратите, кстати, внимание на то, что в нашем примере (массив, являющийся вторым элементом массива ) короче остальных массивов (и поэтому на картинках отсутствует элемент в правом нижнем углу). Это общее правило питона: питон не требует, чтобы внутренние массивы были одинаковой длины
Вы вполне можете внутренние массивы делать разной длины, например:
x = , , , [], ]
здесь нулевой массив имеет длину 4, первый длину 2, второй длину 3, третий длину 0 (т.е. не содержит ни одного элемента), а четвертый длину 1. Такое бывает надо, но не так часто, в простых задачах у вас будут все подмассивы одной длины.
(На самом деле даже элементы одного массива не обязаны быть одного типа. Можно даже делать так: , здесь нулевой элемент массива — сам является массивом, а еще два элемента — просто числа. Но это совсем редко бывает надо.)
Создание матрицы
Вариант 1: Строгое задание элементов матрицы
arr = , ]
arr = , ]
Вариант 2. Создание в памяти матрицы заданного размера, заполненной некоторыми начальными значениями (например, нулями)
НЕВЕРНЫЙ способ (так делать точно не надо)
row = * M
A = * N
ДЕЛАЕМ ПРАВИЛЬНО!
Чтобы создать правильно матрицу, необходимо заставить компилятор создать все строки в памяти как разные объекты.
Для этого необходимо сначала создать пустой список, а затем в цикле добавлять к нему новые строки с помощью метода
N = 3 M = 2 A = [] for i in range(N): A.append(*M)
сделать то же самое можно с помощью генератора
N = 3 M = 2 A = *M for i in range(N) ]
Заполнение матрицы произвольными значениями
После создания матрицы можно заполнить ее произвольными значениями. Так как каждый элемент имеет два индекса, то необходимо использовать вложенные циклы
for i in range(N):
for j in range(M):
A = ...
Вывод матрицы на экран
Вариант 1. Простейший способ
Вывод матрицы в одну строку
print(A)
Вариант 2.
Для обработки и вывода списка, как правило, используется два вложенных цикла. Первый цикл по номеру строки, второй цикл — по элементам внутри строки.
Для того, чтобы вывести матрицу на экран построчно, разделяя числа пробелами внутри одной строки, необходимо написать такой фрагмент:
for i in range(len(A)): # len(A) - возвращает количество строк в матрице А
for j in range(len(A)): # len(A) - возвращает количество элементов в строке i
print(A, end = ' ')
print() # делаем переход на новую строку после вывода на экран строки
То же самое, но циклы не по индексу, а по значениям списка (цикл for умеет делать перебор всех элементов в списке (массиве), строке):
for row in A: # делаем перебор всех строк матрицы A
for elem in row: # перебираем все элементы в строке row
print(elem, end = ' ')
print()
Для вывода одной строки можно воспользоваться методом :
for row in A:
print(' '.join(list(map(str, row))))
Сортировка, поиск, подсчет¶
| Команда | Описание |
|---|---|
| sort(a) | отсортированная копия массива |
| lexsort(keys) | Perform an indirect sort using a sequence of keys. |
| argsort(a) | аргументы, которые упорядочивают массив |
| array.sort() | сортирует массив на месте (метод массива) |
| msort(a) | копия массива отсортированная по первой оси |
| sort_complex(a) | сортировка комплексного массива по действительной части, потом по мнимой |
| argmax(a) | индексы максимальных значений вдоль оси |
| nanargmax(a) | индексы максимальных значений вдоль оси (игнорируются NaN). |
| argmin(a) | индексы минимальных значений вдоль оси |
| nanargmin(a) | индексы минимальных значений вдоль оси (игнорируются NaN). |
| argwhere(a) | массив индексов ненулевых элементов. данные сгруппированы по элементам(,….) |
| nonzero(a) | массивы индексов ненулевых элементов. сгруппированы по размерностям (индексы X, индексы Y, т.д.) |
| flatnonzero(a) | индексы ненулевых элементов в плоской версии массива |
| where(condition, ) | возвращает массив составленный из элементов x (если выполнено условие) и y (в противном случае). Если задано только condition, то выдает его «не нули». |
| searchsorted(a, v) | индексы мест, в которые нужно вставить элементы вектора для сохранения упорядоченности массива |
| extract(condition, a) | возвращает элементы (одномерный массив), по маске (condition) |
| count_nonzero(a) | число ненулевых элементов в массиве |
7.1.1. Значения -inf, inf и nan
Возможно вы обратили внимание на то, что когда мы вычисляли натуральный логарифм массива, среди значений которого был ноль, не появилось абсолютно никакой ошибки, а сам логарифм стал равен значению (минус бесконечность). Убедимся в этом еще раз:. Более того, в NumPy мы даже можем делить на ноль:
Более того, в NumPy мы даже можем делить на ноль:
NumPy предупредил нас о том, что встретил деление на ноль, но тем не менее выдал ответ (плюс бесконечность). Дело в том, что с математической точки зрения все абсолютно верно — если вы что-то делите на бесконечно малое значение то в результате получете значение, которое окажется бесконечно большим. Если результатом математической операции является плюс или минус бесконечность, то логичнее выдать значение или чем выдавать ошибку.
В NumPy есть еще одно специальное значение — . Данное значение выдается тогда, когда результат вычислений не удается определить:
Заметьте, что NumPy нас просто предупредил о том, что ему попалось недопустимое значение, но ошибки не возникло. Дело в том, что в реальных вычислениях значения , или встречается очень часто, поэтому появление этого значения проще обрабатывать специальными методами (функции и ), чем постоянно лицезреть сообщения об ошибках.
Новичкам, довольно трудно привыкнуть, к тому что в недрах компьютера вся арифметика на самом деле является двоичной и с этим связано очень много казусов. Во первых не совсем понятно, когда ждать появления значений и :
Число 1.633123935319537e+16 появилось потому что в NumPy выполняются арифметические, а не символьные вычисления, т. е. число π хранится в памяти компьютера не как знание о том, что это математическая константа с бесконечным количеством десятичных знаков после запятой, а как обычное число с десятичной точкой (десятичная дробь) равная числу π с очень маленькой, но все же, погрешностью:
NumPy отличает предельные случаи, когда вычисления выполнить невозможно, например, деление на ноль. В таких случаях появляются значения , и . Если из-за самых незначительных погрешностей вычисления все же возможны, то NumPy их обязательно выполнит. В этих случаях вместо значений или у вас будут появляться самые маленькие или самые большие числа, которые возможно представить на вашем компьютере.
Тем не менее и на этом сюрпризы не заканчиваются. Если число 1.633123935319537e+16 является самым больши, которое может появиться при вычислениях, оно вполне ожидаемо должно появиться в самых разных ситуациях. Например:
То, есть какая-то, длинная арифметика все же доступна — очень хорошая новость, для лбителей криптографии и теории чисел. Но иногда:
В заключение могу лишь сказать, что все предельные случаи требуют кардинальных решений. Некоторые решения имеются в самом NumPy, некоторые предоставляют другие пакеты. Если вам необходимы точные решения, то лучше обратиться к системам компьютерной алгебры и символьных вычислений, например пакету SymPy — маленький, но мощьный пакет Python для символьных вычислений. Если вы решили отправиться в самые дебри теории чисел, алгебры и криптографии, то лучшим решением окажется программа GAP. Программа GAP не является программой Python, но имеет Python интерфейс в замечательной программе Sage, которая определенно заслуживает вашего внмания.
3.4. Суммы, разности, произведения
- Произведение элементов массива по заданной оси.
- Сумма элементов массива по заданной оси.
- Произведение элементов массива по заданной оси в котором элементы NaN учитываются как 1.
- Сумма элементов массива по заданной оси в котором элементы NaN учитываются как 0.
- Возвращает накопление произведения элементов по заданной оси, т.е. массив в котором каждый элемент является произведением предшествующих ему элементов по заданной оси в исходном массиве.
- Возвращает накопление суммы элементов по заданной оси, т.е. массив в котором каждый элемент является суммой предшествующих ему элементов по заданной оси в исходном массиве.
- Возвращает накопление произведения элементов по заданной оси, т.е. массив в котором каждый элемент является произведением предшествующих ему элементов по заданной оси в исходном массиве. Элементы NaN в исходном массиве при произведении учитываются как 1.
- Возвращает накопление суммы элементов по заданной оси, т.е. массив в котором каждый элемент является суммой предшествующих ему элементов по заданной оси в исходном массиве. Элементы NaN в исходном массиве при суммировании учитываются как 0.
- Возвращает n-ю разность вдоль указанной оси.
- Разность между последовательными элементами массива.
- Дискретный градиент (конечные разности вдоль осей) массива .
- Векторное произведение двух векторов.
- Интегрирование массива вдоль указанной оси методом трапеций.
Произведение матриц
Выбор оператора для поэлементного применения — это странный аспект работы с . В большинстве инструментов для анализа данных оператор обозначает произведение матриц. Он применяется к обоим массивам. В NumPy же подобное произведение обозначается функцией . Эта операция не поэлементная.
Каждый элемент результирующей матрицы — сумма произведений каждого элемента соответствующей строки в первой матрице с соответствующим элементом из колонки второй. Рисунок ниже показывает процесс произведения матриц (для двух элементов).

Еще один вариант записи произведения матриц — использование одной из двух матриц в качестве объекта функции .
Но поскольку произведение матриц — это не коммутативная операция, порядок операндов имеет значение. В данном случае A*B не равняется B*A.
Дискретное преобразование Фурье (numpy.fft)¶
| Прямое преобразование | Обратное преобразование | Описание |
|---|---|---|
| fft(a) | ifft(a) | одномерное дискретное преобразование Фурье |
| fft2(a) | ifft2(a) | двумерное дискретное преобразование Фурье |
| fftn(a) | ifftn(a) | многомерное дискретное преобразование Фурье |
| rfft(a) | irfft(a) | одномерное дискретное преобразование Фурье (действительные числа) |
| rfft2(a) | irfft2(a) | двумерное дискретное преобразование Фурье (действительные числа) |
| rfftn(a) | irfftn(a) | многомерное дискретное преобразование Фурье (действительные числа) |
| hfft(a) | ihfft(a) | преобразование Фурье сигнала с Эрмитовым спектром |
| fftfreq(n) | частоты дискретного преобразования Фурье | |
| fftshift(a) | ifftshift(a) | преобразование Фурье со сдвигом нулевой компоненты в центр спектра |
Создание, вывод и ввод матрицы в Питоне
- Таким образом, получается структура из вложенных списков, количество которых определяет количество строк матрицы, а число элементов внутри каждого вложенного списка указывает на количество столбцов в исходной матрице.
Рассмотрим пример матрицы размера 4 х 3:
matrix = -1, , 1,
-1, , 1,
, 1, -1,
1, 1, -1
|
Данный оператор можно записать в одну строку:
matrix = -1, , 1, -1, , 1, , 1, -1, 1, 1, -1 |
Вывод матрицы можно осуществить одним оператором, но такой простой способ не позволяет выполнять какой-то предварительной обработки элементов:
print(matrix) |
Результат:
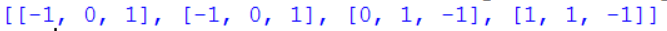
Для вывода матрицы в виде таблицы можно использовать специально заготовленную для этого процедуру:
- способ:
1 2 3 4 5 |
def printMatrix ( matrix ):
for i in range ( len(matrix) ):
for j in range ( len(matrixi) ):
print ( "{:4d}".format(matrixij), end = "" )
print ()
|
В примере i – это номер строки, а j – номер столбца;len(matrix) – число строк в матрице.
способ:
1 2 3 4 5 |
def printMatrix ( matrix ):
for row in matrix:
for x in row:
print ( "{:4d}".format(x), end = "" )
print ()
|
Внешний цикл проходит по строкам матрицы (row), а внутренний цикл проходит по элементам каждой строки (x).
Для инициализации элементов матрицы случайными числами используется алгоритм:
1 2 3 4 5 6 |
import random
for i in range(N):
for j in range(M):
matrixij = random.randint ( 30, 60 )
print ( "{:4d}".format(matrixij), end = "" )
print()
|