Построение сетевого графика онлайн программа. как выглядит график
Содержание:
Методы оптимизации сетевого графика
Сетевой график проектной реализации связан с содержанием уникальной задачи, параметрами времени и пространства, в которых выполняется проект. Данной деятельности присущи все традиционные функции управления без исключения. С этой точки зрения процесс можно разделить на этапы, в которых весомую долю занимает планирование. Далее вашему вниманию представляется упрощенная блок-схема функциональных этапов управления проектом.
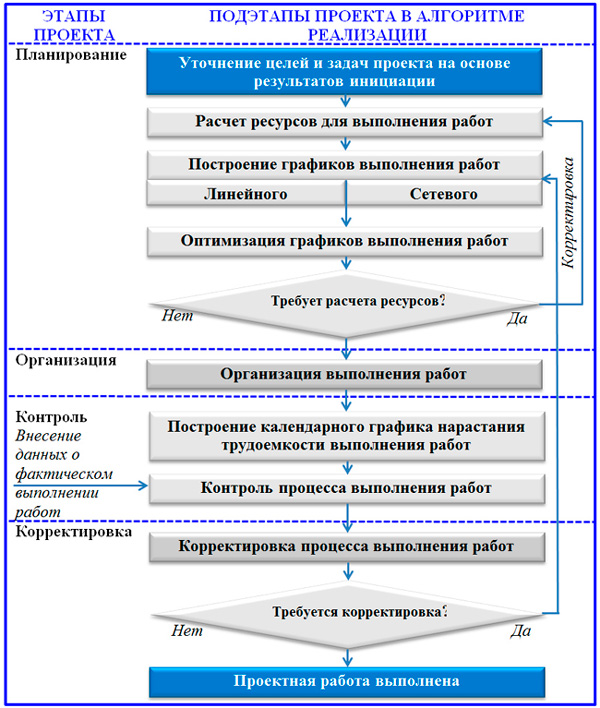Функционально-процессная блок-схема управления проектом
На текущий момент нас интересует оптимизация сетевого графика как подэтап процесса планирования проектной задачи. Это связано с тем, что после сбора информации о работах и ограничениях разработка визуальной модели в форме сетевой диаграммы подразумевает дальнейшее ее улучшение с использованием методов расчета расписания. Основных методов два: метод критического пути (сокращенно МКП) и анализ расписания по методу PERT.
При использовании МКП производится последовательный расчет наиболее ранних и самых поздних сроков работ по проекту. Далее устанавливается размер полного резерва, при этом критическими работами считаются действия, имеющие нулевой полный резерв. Наконец, рассчитываются временные резервы для выполнения операций, и в качестве самого длинного пути сети выбирается критический путь. Критических путей может быть несколько. Оптимизация сетевого графика методом критического пути применяется для следующих моделей диаграммы:
- для моделей с дискретным и непрерывным временем;
- для моделей с простым отношением предшествования;
- в сетях с обобщенными связями.
Метод оценки и анализа программ (PERT) служит вторым методом, по которому проводится оптимизация сетевого графика. Его основные отличия от МКП основаны на допущении, что длительность работ носит случайный характер, и для целей оценки и анализа сроков следует учитывать неопределенность временного параметра работ проекта. Также делается допущение о независимости всех случайных величин продолжительности критического пути. Для этих целей на основе метода математической статистики и теории вероятности используется β-распределение и оценка параметров распределения с трех экспертных позиций: оптимистичной, пессимистичной и наиболее вероятной.
Корректировка сетевого графика и сокращение общей продолжительности проекта входят в состав ключевых задач проект-менеджера. МКП дает возможность рассчитать оптимальные сроки выполнения проекта, но не позволяет найти инструменты для более действенного сокращения его продолжительности. В этом отношении метод критического пути не обладает достаточной гибкостью. Метод PERT также не лишен недостатков. Во-первых, он нацеливает в основном на оптимистический вариант оценки, во-вторых, PERT в меньшей степени применим к небольшим проектным задачам.
Для эффективной корректировки лучше всего подходят такие современные методы, как метод критической цепи и методы сжатия
Им мы намерены уделить внимание в отдельной статье. Все названные модели и методы являются предметной зоной компетенций PM, владея которыми, менеджеру проще демонстрировать свою эффективность, достигая результата проекта в условиях временных и ресурсных ограничений
Корректировка сетевой модели
Корректировка сетевой модели может проводиться и в первом случае, если имеется возможность для повышения эффективности реализации запланированных операций.
В сетевом планировании выделяют три способа корректировки модели:
- изменение сроков выполнения критических операций за счет привлечения дополнительных ресурсов, в качестве которых могут выступать денежные средства, материалы или человеческие ресурсы;
- изменение сроков выполнения критических операций за счет привлечения исполнителей, занятых на других операциях, при сохранении изначальных параметров ресурсов;
- изменение сроков выполнения операций за счет совмещения их выполнения.
В первом случае корректировка сетевой модели осуществляется без изменения сетевой диаграммы. Данный подход чаще всего практикуется в тех случаях, когда для выполнения операций остаются свободные ресурсы, не задействованные в других операциях.
Во втором случае сетевая диаграмма также остается неизменной. Данный подход используется в тех случаях, когда возможно увеличить срок выполнения операций, не принадлежащих к критическому пути.
Третий случай применяется при невозможности использования дополнительных ресурсов и подразумевает повторное построение сетевой диаграммы.
После проведения корректировки осуществляется построение альтернативной сетевой модели.
Следует отметить, что в корректировке сетевой модели заключается фундаментальное назначение сетевого планирования. Благодаря построению сетевых моделей уже на ранней стадии планирования могут быть выявлены условия, свидетельствующие о том, что в заданные директивные сроки проект невозможно будет выполнить. Поэтому для получения приемлемых с точки зрения целей проекта сроков возможно осуществление коррекции расписания операций по принципу изменения продолжительности критических операций. Таким образом, если проект или заданный план действий не укладывается в директивные сроки, то предпринимается попытка сократить сроки выполнения критических операций за счет изменения их зависимости от первоначально заданных параметров их выполнения.
Литература
- Черняк В.З., Довдиенко И.В. Методы принятия управленческих решений. – М.: Академия, 2013.
- Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г., Полковников А.В. Управление проектами. – М.: Омега-Л, 2012.
- Новыш Б.В., Шешолко В.К., Шаститко Д.В. Экономико-математические методы принятия решений. – М.: Инфра-М, 2013.
- Урубков А.Р., Федотов И.В. Методы и модели оптимизации управленческих решений. – М.: изд-во АНХ, 2011.
- Сухачев К.А., Колосова Е.С. Практика применения технологий календарно-сетевого планирования. // Нефтегазовая вертикаль. – 2010. – №11 (240), июнь 2010. – С. 28-30.
Расчет графика: прямой анализ
Оценка временных затрат на выполнение одной операции производится на основании нормативных трудозатрат. Благодаря прямому или обратному методу расчета, можно довольно быстро сориентироваться в порядке выполнения работ и выявить критические шаги.
Прямой анализ позволяет определить ранние сроки начала всех операций. Обратный — дает представление о поздних сроках. Кроме того, с помощью обеих методик анализа можно не только установить критический путь, но и выявить временные интервалы, на которые можно задержать выполнение отдельных работ без срыва общих сроков реализации проекта.
Прямой анализ рассматривает проект от начала до конца (если говорить о составленном графике, то движение по нему происходит слева направо). Во время движения по всем цепочкам операций происходит наращение времени выполнения всего комплекса работ. Прямой расчет сетевого графика предполагает, что каждая последующая операция начинается в тот момент, когда заканчиваются все предшествующие ей. При этом необходимо помнить, что следующая работа стартует в тот момент, когда закончится самая длительная из непосредственно предшествующих. На каждом шаге прямого анализа добавляется время выполнения расчетной операции. Так мы получаем значения раннего начала (ES) и раннего окончания работ (EF).
Но нужно быть внимательным: раннее окончание предшествующей операции становится ранним началом последующей только в том случае, если она не является слиянием. В этом случае стартом станет раннее окончание самой затяжной из предыдущих работ.
Графики
Графики разные по строительству скачать :
Примеры графиков производства работ:
1 График производства земляных работ, пример скачать jpg, скачать rar
2 График производства работ по строительству школы, пример скачать doc
3 График производства работ по объекту: Центральный тепловой пункт ЦТП, пример скачать xls, скачать zip
4 График производства работ на комплекс работ по устройству наружного освещения, кабельной сети и декоративной подсветки, пример скачать xls, скачать zip
5 График производства работ на реконструкцию, пример скачать xls, скачать zip
Примеры календарных графиков:
1 Календарный график производства работ, календарный график движения рабочей силы, машин и механизмов на прокладку полиэтиленовых труб, бланк (в формате Компас V15.1) скачать frw
2 Календарный график выполнения работ по объекту, пример скачать xls.
3 Календарный график, пример скачать zip, скачать pdf.
4 Календарный план производства работ на тепловые сети, пример скачать zip, скачать doc.
5 Календарный план производства работ на установку опор ВОЛС, пример скачать zip, скачать doc.
6 Месячно-суточный график выполнения работ, пример скачать xls, скачать zip
Примеры прочих графиков:
1 График подготовки и сдачи исполнительной технической документации ИТД, пример скачать xls, скачать zip
2 График потребности в рабочих кадрах и основных строительных машинах, пример скачать xls, скачать zip
3 График поступления на объект строительных конструкций, изделий и материалов, пример скачать xls, скачать zip
4 График поставок материалов и оборудования, пример скачать doc, скачать zip
5 График движения рабочей силы, пример скачать xls, скачать zip
5а График движения персонала на строительстве, пример скачать xls, скачать zip
6 График выполнения СМР, пример скачать pdf, скачать zip
7 График кирпичной кладки, пример скачать xls, скачать zip
8 Плановый график расстановки специалистов подрядной организации, пример скачать xls, скачать zip
9 Фактический график расстановки специалистов подрядной организации, пример скачать xls, скачать zip
10 График (табель) учёта фактически отработанных дней специалистов подрядной организации, пример скачать xls+приложение, скачать zip
Вернуться к разделу: «Акты, схемы протокола и прочее».
Смотрите состав исполнительной в разделе: «Состав исполнительной»
Скачивайте акты, протокола и другое в разделе: «Акты и прочее»
Скачивайте полезные книги, ГОСТы, СнИПы в разделе: «ГОСТы и книги
Масштабный сетевой график
- Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
- Построить масштабный сетевой график.
- Оценить вероятность выполнения всего комплекса работ за 30 дней.
- Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.
| Код работы ( i,j) | Продолжительность | |
| tmin (i,j) | tmax (i,j) | |
| 1,2 | 5 | 10 |
| 1,4 | 2 | 7 |
| 1,5 | 1 | 6 |
| 2,3 | 2 | 4,5 |
| 2,8 | 9 | 19 |
| 3,4 | 1 | 3,5 |
| 3,6 | 9 | 19 |
| 4,7 | 4 | 6,5 |
| 5,7 | 2 | 7 |
| 6,8 | 7 | 12 |
| 7,8 | 5 | 7,5 |
Решение находим с помощью сервиса Сетевая модель
. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная tmax(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение tож(i,j) оценивается по формуле
tож(i,j)=(3 tmin(i,j)+2 tmax (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(tmax(i,j)-tmin(i,j))2Рассчитаем ожидаемое значение и показатель дисперсии.
tож(1,2)=(3*5+2*10)/5=7
tож(1,4)=(3*2+2*7)/5=4
tож(1,5)=(3*1+2*6)/5=3
tож(2,3)=(3*2+2*4,5)/5=3
tож(2,8)=(3*9+2*19)/5=13
tож(3,4)=(3*1+2*3,5)/5=2
tож(3,6)=(3*9+2*19)/5=13
tож(4,7)=(3*4+2*6,5)/5=5
tож(5,7)=(3*2+2*7)/5=4
tож(6,8)=(3*7+2*12)/5=9
tож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25
Полученные данные занесем в таблицу.
Таблица – Сетевая модель.
| Работа ( i,j) | Продолжительность | Ожидаемая продолжительность tож(i,j) | Дисперсия S2(i,j) | |
| tmin (i,j) | tmax (i,j) | |||
| 1,2 | 5 | 10 | 7 | 1 |
| 1,4 | 2 | 7 | 4 | 1 |
| 1,5 | 1 | 6 | 3 | 1 |
| 2,3 | 2 | 4,5 | 3 | 0,25 |
| 2,8 | 9 | 19 | 13 | 4 |
| 3,4 | 1 | 3,5 | 2 | 6,25 |
| 3,6 | 9 | 19 | 13 | 4 |
| 4,7 | 4 | 6,5 | 5 | 0,25 |
| 5,7 | 2 | 7 | 4 | 1 |
| 6,8 | 7 | 12 | 9 | 1 |
| 7,8 | 5 | 7,5 | 6 | 0,25 |
| КПР | Код работы (i,j) | Продолжительность работы t(i, j) | Ранние сроки | Поздние сроки | Резервы времени | |||
| tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | Rп | Rc | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1,2 | 7 | 7 | 7 | |||||
| 1,4 | 4 | 4 | 17 | 21 | 17 | 8 | ||
| 1,5 | 3 | 3 | 19 | 22 | 19 | |||
| 1 | 2,3 | 3 | 7 | 10 | 7 | 10 | ||
| 1 | 2,8 | 13 | 7 | 20 | 19 | 32 | 12 | 12 |
| 1 | 3,4 | 2 | 10 | 12 | 19 | 21 | 9 | |
| 1 | 3,6 | 13 | 10 | 23 | 10 | 23 | ||
| 2 | 4,7 | 5 | 12 | 17 | 21 | 26 | 9 | |
| 1 | 5,7 | 4 | 3 | 7 | 22 | 26 | 19 | 10 |
| 1 | 6,8 | 9 | 23 | 32 | 23 | 32 | ||
| 2 | 7,8 | 6 | 17 | 23 | 26 | 32 | 9 | 9 |
кр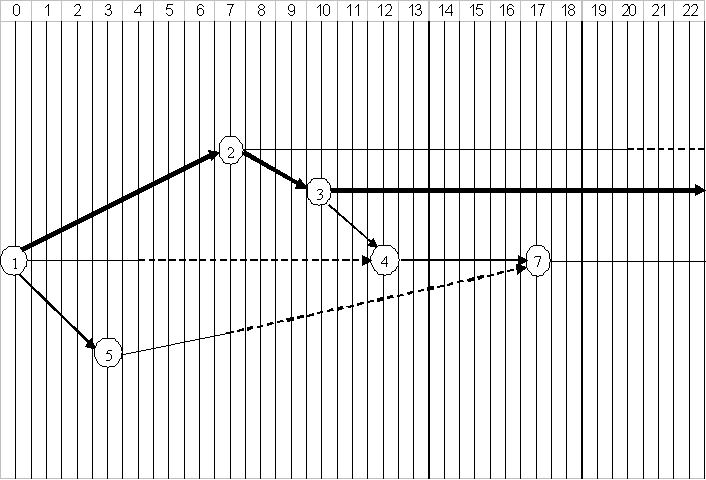
P(tкр
где Z=(Т-Ткр)/SкрZ- нормативное отклонение случайной величины, Sкр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.
| Z | F(Z) | Z | F(Z) | Z | F(Z) |
| 0.0000 | 1.0 | 0.6827 | 2.0 | 0.9643 | |
| 0.1 | 0.0797 | 1.1 | 0.7287 | 2.1 | 0.9722 |
| 0.2 | 0.1585 | 1.2 | 0.7699 | 2.2 | 0.9786 |
| 0.3 | 0.2358 | 1.3 | 0.8064 | 2.3 | 0.9836 |
| 0.4 | 0.3108 | 1.4 | 0.8385 | 2.4 | 0.9876 |
| 0.5 | 0.3829 | 1.5 | 0.8664 | 2.5 | 0.9907 |
| 0.6 | 0.4515 | 1.6 | 0.8904 | 2.6 | 0.9931 |
| 0.7 | 0.5161 | 1.7 | 0.9104 | 2.7 | 0.9949 |
| 0.8 | 0.5763 | 1.8 | 0.9281 | 2.8 | 0.9963 |
| 0.9 | 0.6319 | 1.9 | 0.9545 | 2.9 | 0.9973 |
Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S2(Lкр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(Lкр)=2,5
p(tкр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:
Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.
Последовательность действий по моделированию
Шаг первый
Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.
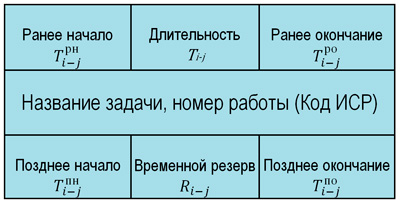Схема изображения работы на сетевом графике
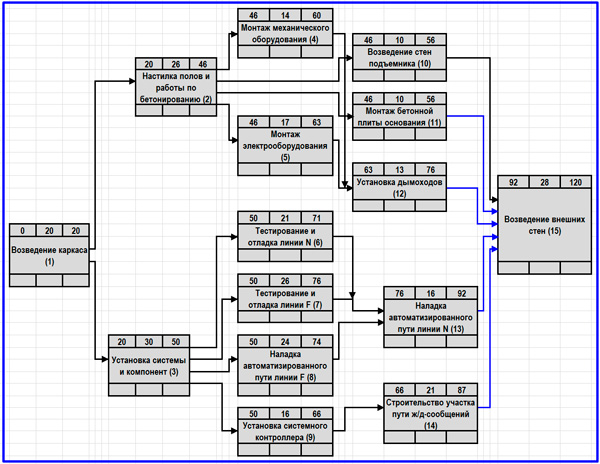Результат первого этапа построения сетевого графика
В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность. Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом.
Шаг второй
Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят. Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее.
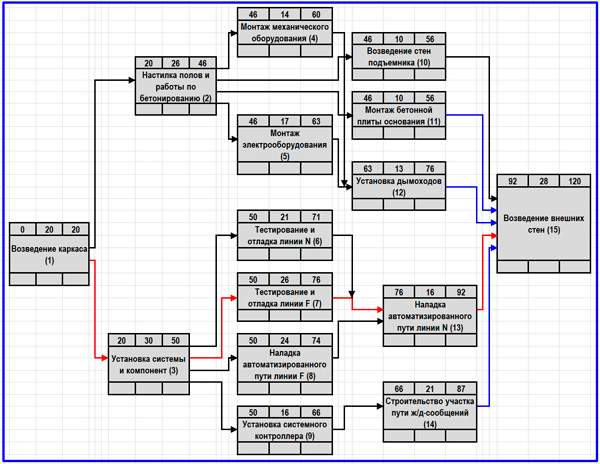Схема сетевого графика с выделенным критическим путем
Шаг третий
Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.
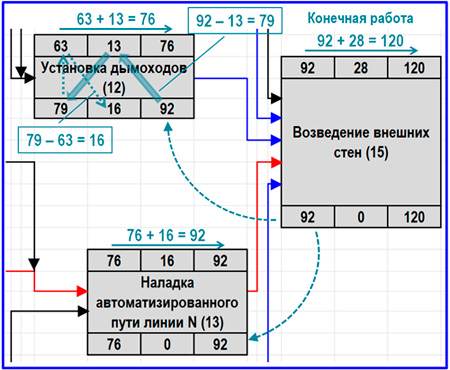Схема расчета поздних начал и окончаний вне критического пути
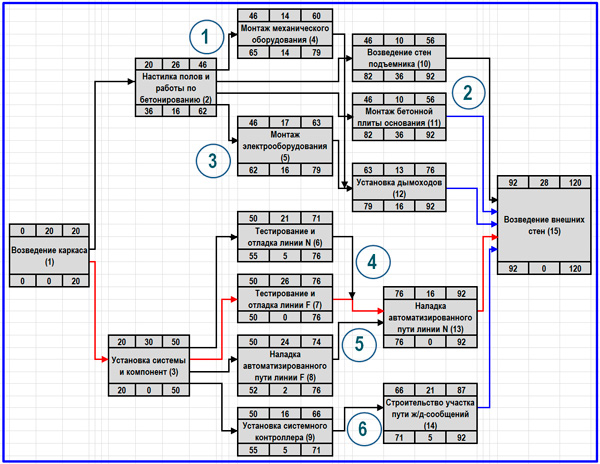Итоговый вид сетевого графика
Шаг четвертый
Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности
Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика
- R пути под номером 1 = 120 – 101 = 19;
- R пути под номером 2 = 120 – 84 = 36;
- R пути под номером 3 = 120 – 104 = 16;
- R пути под номером 4 = 120 – 115 = 5;
- R пути под номером 5 = 120 – 118 = 2;
- R пути под номером 6 = 120 – 115 = 5.
Построение сетевого графика
В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.
В таблицу сведем следующие данные по каждой операции:
- номер операции;
- предшествующие операции;
- количество исполнителей;
- продолжительность операции в днях.
В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.
|
Номер операции |
Предыдущие операции |
Кол-во исполнителей, чел. |
Продолжительность, дни |
|---|---|---|---|
|
1. |
— |
10 |
1 |
|
2. |
1 |
2 |
3 |
|
3. |
1 |
3 |
1 |
|
4. |
1 |
2 |
4 |
|
5. |
4 |
1 |
0,5 |
|
6. |
3 |
3 |
2 |
|
7. |
5 |
2 |
0,5 |
|
8. |
2,7,6 |
10 |
0,5 |
|
9. |
9 |
10 |
0,5 |
|
10. |
9 |
1 |
3 |
|
11. |
9 |
2 |
4 |
|
12. |
9 |
2 |
2 |
|
13. |
9 |
2 |
3 |
|
14. |
12 |
2 |
2 |
|
15. |
13 |
3 |
2 |
|
16. |
10,11,14,15 |
10 |
0,5 |
|
17. |
16 |
10 |
0,5 |
|
18. |
17 |
2 |
2 |
|
19. |
18 |
2 |
3 |
|
20. |
17 |
2 |
2 |
|
21. |
17 |
2 |
3 |
|
22. |
21 |
3 |
1 |
|
23. |
20 |
2 |
2 |
|
24. |
19,22,23 |
10 |
0,5 |
|
25. |
24 |
10 |
0,5 |
|
26. |
25 |
5 |
1 |
|
27. |
26 |
5 |
3 |
|
28. |
25 |
3 |
2 |
|
29. |
28 |
3 |
2 |
|
30. |
25 |
2 |
4 |
|
31. |
27,29,30 |
10 |
0,5 |
|
32. |
31 |
10 |
0,5 |
|
33. |
32 |
7 |
1 |
|
34. |
32 |
2 |
1 |
|
35. |
33,34 |
10 |
1 |
На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.
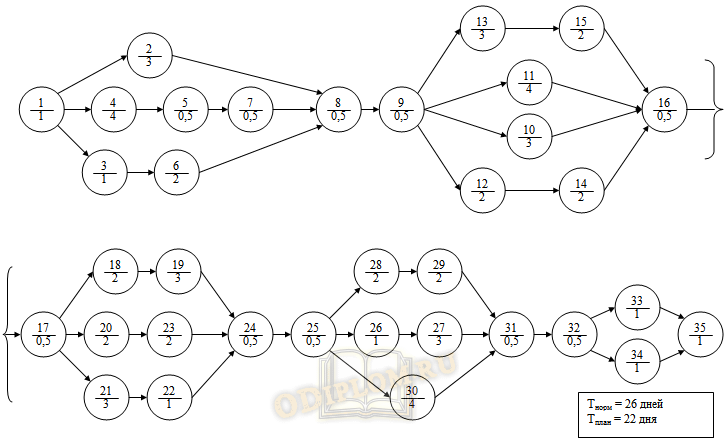
Сетевой график, пример
Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.
В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.
Для соблюдения запланированных сроков произведем корректировку сетевого графика.
В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.
После корректировки осуществим построение альтернативного сетевого графика.
Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:
Q = N * t
Q4 = 2*4 = 8 ч/дн
Q13 = 2*3 = 6 ч/дн
Q18 = 2*2 = 4 ч/дн
В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.
В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.
В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.
В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:
26 – 2 – 1 – 1 = 22 дня.
Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.
Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.
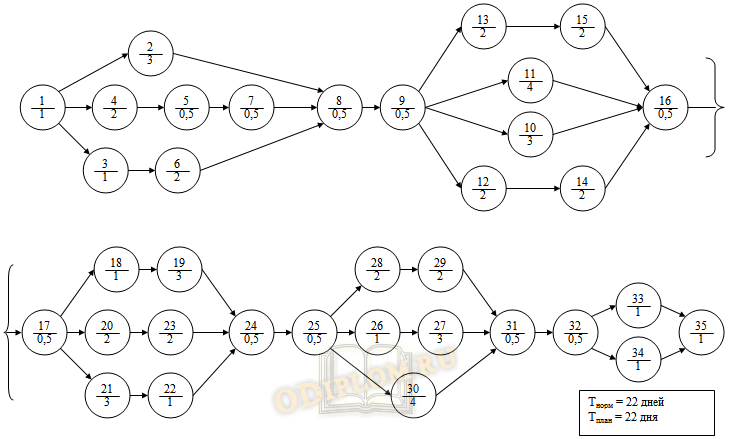
Альтернативный сетевой график
Автоматизация процесса
На сегодняшний день мало кто из проектных менеджеров вручную построения сетевых графиков — это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.
Кратко рассмотрим самые распространенные программы:
-
Microsoft Project 2002
— офисный продукт, в котором очень удобно рисовать схемы. Но проводить расчеты немного неудобно. Для того чтобы совершить даже самое простое действие, нужен немалый багаж знаний. Скачивая программу, позаботьтесь о приобретении инструкции по пользованию к ней. -
SPU v2.2.
Очень распространенный бесплатный софт. Вернее, даже не программа, а файл в архиве, для использования которого не нужна установка. Изначально она была разработана для выпускной работы одного студента, но оказалась настолько полезной, что автор выложил ее в сеть. -
NetGraf
— еще одна разработка отечественного специалиста из Краснодара. Очень легка, проста в использовании, не требует установки и огромного багажа знаний, как с ней управляться. Плюсом является то, что поддерживает импорт информации из других текстовых редакторов. - Часто можно встретить вот такой экземпляр — Borghiz
. О разработчике мало что известно, как и о том, как пользоваться программой. Но по примитивному методу «тыка» ее можно освоить. Главное, что она работает.
Назначение сервиса
параметров сетевой модели
- ранний срок свершения события , поздний срок свершения события, ранний срок начала работы, ранний срок окончания работы, поздний срок начала работы, поздний срок окончания работы;
- резерв времени на свершение события, полный резерв времени, свободный резерв времени;
- продолжительность критического пути;
Пример
. Описание проекта в виде перечня выполняемых операций с указанием их взаимосвязи приведено в таблице. Построить сетевой график, определить критический путь, построить календарный график.
| Работа (i,j) | Количество предшествующих работ | Продолжительность t ij | Ранние сроки: начало t ij Р.Н. | Ранние сроки: окончание t ij Р.О. | Поздние сроки: начало t ij П.Н. | Поздние сроки: окончание t ij П.О. | Резервы времени: полный t ij П | Резервы времени: свободный t ij С.В. | Резервы времени: событий R j |
| (0,1) | 8 | 8 | 8 | ||||||
| (0,2) | 3 | 3 | 1 | 4 | 1 | 1 | |||
| (1,3) | 1 | 1 | 8 | 9 | 8 | 9 | |||
| (2,3) | 1 | 5 | 3 | 8 | 4 | 9 | 1 | 1 | |
| (2,4) | 1 | 2 | 3 | 5 | 13 | 15 | 10 | 10 | |
| (3,4) | 2 | 6 | 9 | 15 | 9 | 15 |
Независимый резерв времени работы
R ij Н — часть полного резерва времени, если все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки.
Использование независимого резерва времени не влияет на величину резервов времени других работ. Независимые резервы стремятся использовать, если окончание предыдущей работы произошло в поздний допустимый срок, а последующие работы хотят выполнить в ранние сроки. Если R ij Н ≥0, то такая возможность имеется. Если R ij Н
Итак, в предыдущей статье мы разобрались, и для чего она, собственно, нужна рядовому пользователю. Напомним основные понятия данного урока:
- — локальная сеть – это система соединенных линиями связи вычислительных устройств, предназначенная для передачи информации конечному числу абонентов;
- — существует три основных вида топологии локальных сетей, на основе которых строятся более сложные структуры локальной связи;
- — по способу взаимодействия компьютеров локальные сети бывают одноранговыми (когда все подключенные к сети ПК равноправны) и с выделенным сервером.
В данной статье мы рассмотрим, как создать локальную сеть с одинаковым правом доступа всех ее пользователей.
К достоинствам такой сети относятся простота конструкции (настройка домашней сети вполне «по зубам» новичку) и экономическая доступность оборудования, но спектр функциональных возможностей такой сети весьма ограничен.
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
