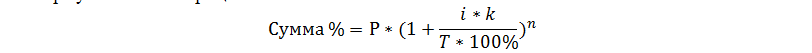Процент

Насколько число меньше другого в процентах

К примеру: обычная стоимость порошка – 500 рублей. По акции, цену снизили до 480 рублей. Насколько цена по акции, меньше первоначальной в процентах? Вначале находят процентную составляющую акционной цены от базовой, а затем находиться их разница. Составляем пропорцию:

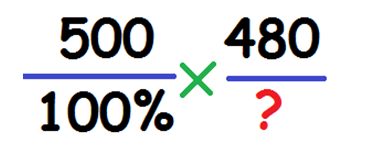
Вычисляем по формуле: (480*100)/500=96. 100%-96%=4%. Цена по акции меньше первоначальной на 4%.

Насколько число больше другого в процентах. Пример: клавиатура стоила 300 рублей, а после повышения курса доллара, цена выросла до 390 рублей. Насколько изменилась цена на клавиатуру в процентах? Вначале находиться общая процентная ставка новой цены, относительно первоначальной, затем вычисляется их разница. Составляем пропорцию:

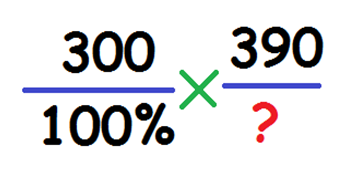
Вычисляем по формуле: (390*100)/300=130. 130%-100%=30%. Цена выросла на 30%.

Неизвестное число больше известного на определенный процент. Пример: товар в магазине, дороже товара на складе на 15%.  Цена сахара на складе – 50 рублей и приравнивается к 100%. Магазинная цена  – 100%+15%=115%. Вычисляем по формуле: (115*50)/100=57,5

Неизвестное число меньше известного на заданный процент. Пример: оптом на 5% дешевле. Цена за розницу – 60 рублей и равна 100 процентам, за опт – 100%-5%=95%. Составляем пропорцию:

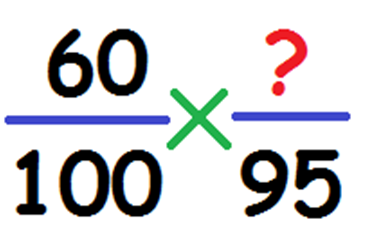
Вычисляем по формуле: (60*95)/100=57

Процент между двумя числами. Ситуация, когда известно число, составляющее 100% и число, составляющее некую долю от первоначального. Пример: ожидалась партия в 60 коробок, а завезли 53. На сколько процентов выполнился план. Составляем пропорцию:

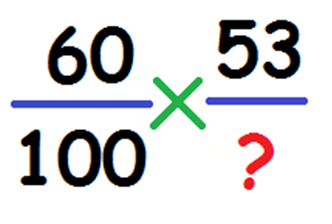
Вычисляем по формуле: (53*100)/60=88,3

Самая сложная «задача» — не запутаться в составлении пропорции.

Формулы для определения необходимой доли от суммы

Есть несколько способов найти требуемый процент от любого числа.

Первый способ состоит в делении нужной суммы на 100, после чего полученный результат умножается на % который необходимо определить.

Формула расчёта в данном случае выглядит так:

A / 100 * B =

В данной формуле A – это базовое число, из которого нужно извлечь долю.

B – процент, который необходимо высчитать в числовом выражении.

Например, в каком-либо магазине вам отдают товар, цена которого 500 рублей, за 70% его стоимости. Используя приведённую выше формулу, высчитываем, сколько нам необходимо заплатить в конечном итоге (или сколько будет 70% от 500 рублей):

500 / 100 * 70 = 350 рублей

Таким образом, мы сможем приобрести нужный товар за 350 рублей.

Второй способ состоит в умножении базового числа A на коофициент 0,B

Где А – это базовое число, а B – количество процентов, которые необходимо определить.

Формула имеет следующую форму:

A * 0,B =

В случае упомянутого выше примера с 70% стоимости от 500 высчитываем стоимость товара:

500 * 0,70 = 350

Третий способ состоит в умножении базового числа на количество процентов, после чего полученный результат делим на 100.

Формула выглядит следующим образом:

A * B  / 100 =

В нашем случае это:

500 * 70 / 100 = 350

На калькуляторе нужная доля от числа находится ещё проще:

1. Набираете на калькуляторе базовое число (А).
2. Жмёте на умножить, вводите искомое число процентов.
3. После чего жмёте на кнопку %, а затем на кнопку =. Калькулятор тот час же отобразит требуемый результат.

500*70% = (результат)

Что такое проценты?

Это слово произошло от английского словосочетания Pro Centum

Прочитав это словосочетание, вы наверняка обратили внимание, что там присутствует слово цент. От этого и происходит смысл процентов

Как известно, цент — одна сотая часть от доллара. Поэтому 1% — это и есть одна сотая часть от числа.

Сейчас в процентах измеряются многие финансовые показатели:

1. налоги,
2. доли в бизнесе,
3. доходность от инвестиций,
4. премии и штрафы,
5. инфляция.

И не только финансовые:

1. рождаемость и смертность,
2. статистика удачных и неудачных браков,
3. коэффициент полезного действия.

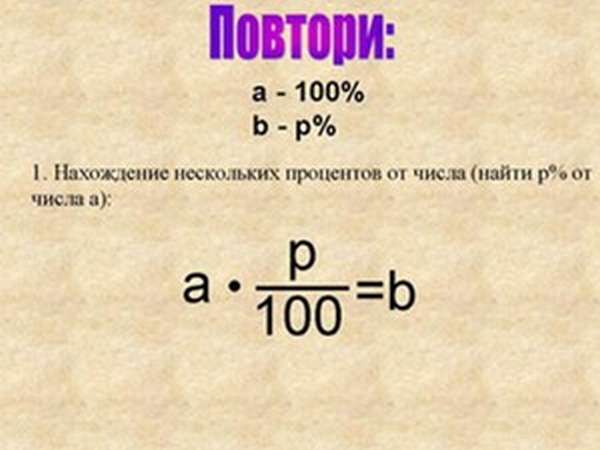Давайте разберёмся более подробно, как посчитать процент от суммы. Мы приведём вам несколько примеров, которые помогут вам все понять.

Пример 1. Водитель таксомоторной службы отработал смену. За день его выручка составила 5 тыс. рублей. Ему необходимо отдать службе такси комиссию с этих заказов — 15%. Чтобы узнать сумму, которую должен заплатить водитель, необходимо 5 тыс. умножить на 15, после чего разделить на 100. Мы получаем результат, равный 750 рублей. Как вы уже догадались, 15% — это 15 частей из ста.

Теперь мы приведём вам обратный пример с тем же водителем такси. Так, за смену он заработал 5 тыс. рублей. Он потратил определённую часть этих денег на обязательные расходы:

1. комиссию службе такси — 750 рублей,
2. мойку автомобиля — 250 рублей,
3. топливо — 1 тыс. рублей.

Итого у водителя остаётся 3 тыс. рублей. Из заработанных 5 тыс. рублей себе он забирает только 3. Теперь наша задача посчитать, какую часть от общей выручки он может смело положить к себе в карман. Для этого нам нужно разделить 3 тыс. на 5 тыс. После чего полученный результат, равный 0,6, умножить на 100%. Получается, водитель забирает себе в карман 60% от общей выручки.

Это интересно: разрядные слагаемые что это?

Пример 2. Четыре акционера открыли бизнес. Спустя год упорной работы он начал приносить доходы. Партнёры решили делить прибыль поровну, то есть каждому достанется по 25% от прибыли. Нам нужно посчитать, сколько денег получит каждый из них.

Допустим, бизнес приносит доход 200 тысяч рублей в месяц. Чтобы посчитать прибыль каждого из акционеров, необходимо умножить 200 тыс. на 25, и разделить на 100. Получаем результат — 50 тыс. рублей.

Пример 3. Конверсия продаж. Менеджер по продажам предлагает услуги своей компании по телефону. За месяц он совершил 800 звонков. Заинтересовались в услугах компании 280 клиентов. Для подсчёта конверсии продаж необходимо 280 разделить на 800, после чего умножить на 100. Результат будет равен 35%.

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Происхождение

В Древнем Риме, задолго до существования десятичной системы счисления, вычисления часто производились с помощью дробей, которые были кратны 1/100. Например, Октавиан Август взимал налог в размере 1/100 на товары, реализовавшиеся на аукционе, это было известно как лат. centesima rerum venalium (сотая доля продаваемых вещей). Подобные расчёты были похожи на вычисление процентов.

При деноминации валюты в средние века вычисления со знаменателем 100 стали более привычными, а с конца XV века до начала XVI века данный метод расчёта стал повсеместно использоваться, судя по содержанию изученных материалов, содержащих арифметические вычисления. Во многих из этих материалов данный метод применялся для расчёта прибыли и убытка, процентных ставок, а также в правиле трёх[неизвестный термин]. В XVII веке данная форма вычислений стала стандартом для представления процентных ставок в сотых долях.

В России понятие процента впервые ввёл Пётр I. Но считается, что подобные вычисления начали применяться в Смутное время, как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек[источник не указан 1412 дней].

Калькулятор и компьютерные программы

Некоторые люди и в школе не совсем уверенно чувствовали себя при необходимости вычислений в столбик, а по прошествии нескольких лет благополучно забыли, как это делается. Им на помощь придет калькулятор. Для нашей операции не потребуется серьезный инженерный калькулятор с множеством функций. Достаточно обычного, который есть в каждом телефоне.

Рассчитать процент на нем несложно. Набираем исходную величину, нажимаем знак «умножить», затем набираем нужное нам количество процентов и нажимаем знак «%». Допустим, есть необходимость высчитать долю оклада, уходящую на налоги. Размер оклада — 30000 рублей, налоги составляют 13%. Берем калькулятор и набираем следующую комбинацию:

30000*13%. Получаем 3900 рублей.

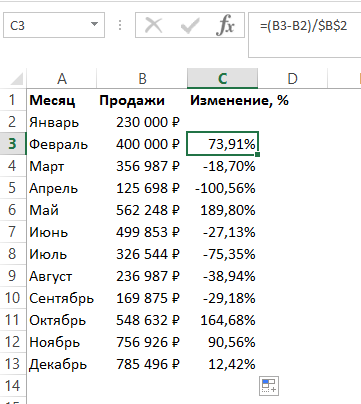
В любой компьютерной программе, например в «Экселе», посчитать проценты не составит труда. Если человек смог освоить такую серьезную программу, с помощью которой можно проводить расчеты любой сложности, то для него будет несложно провести такую элементарную операцию, как расчет процента числа в Excel.

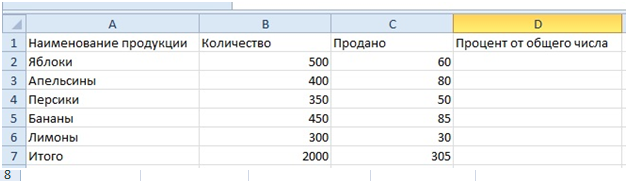
Рассмотрим, как в «Экселе» посчитать процентную долю. В столбец В заносится исходное число, в столбец С — нужное нам количество процентов. В столбец D вносим выражение =C1/B1. После этого нажимается команда «процентный формат». В столбце D появится искомое число. Причем командами «увеличить разрядность» или «уменьшить разрядность» можно довести ответ до нужного нам уровня точности изменением количества знаков после запятой.

Способов, как посчитать процент от числа, много, они разнообразны, и человек с любым уровнем математической подготовки может выбрать для себя наиболее подходящий. Освоив разные методы, вы сможете помочь ребенку при решении задач. Причем не только в математике, но и в других науках. Например, в химии довольно часто приходится находить объемную или массовую долю элемента в веществе или растворе.

Владение вышеописанными навыками поможет вам осознанно подходить к вопросам, связанным с вашим семейным бюджетом. Высчитать процент расходов и сопоставить их с доходами — важнейшая операция для грамотного ведения домашнего хозяйства.

Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой.

Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.

Математическое объяснение

С точки зрения математики и ее основ решение задачи о том, как рассчитать процент от суммы, сводится только к применению простейших правил раскрытия скобок при умножении суммы на единое число и поиска общего знаменателя, который, в общем-то, им и является. Другими словами, представить в формульном выражении это можно так:

a x (b + c) = ab + ac ,

где ab и ac – произведения слагаемых в скобках (b и c) на число (коэффициент) перед скобками a.

Собственно, в пропорции действует тот же метод. Допустим, у нас есть некое число z, представляющее собой 100%, и сумма чисел a и b. Процент, который нужно вычислить, обозначим неизвестным числом y. В таком варианте пропорция принимает вид:

Отсюда простое решение:

((a + b) x 100%)/z = ((a x 100%) + (b x 100%))/z

В скобки действия взяты для того, чтобы подчеркнуть, что операции умножения выполняется в первую очередь, а сложение произведений – во вторую. Такое же действие производится, если изначально сумма чисел составляет 100%.

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

20% = 0,2

500 * 0,2 = 100

Из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

38/0,16 = 38 * 100/16 = 237,5

Значит 237 задачи включили в этот сборник.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: возьмем алгоритм из правила выше:

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 47%

В классе учится 10 девочек — это 47%.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

Формула расчета процента от числа выглядит так:

a = b * ((1 + c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: подставим в формулу данные из условий задачи.

110 * (1 + 12/100) = 110 * 1,12 = 123,2.

Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

Формула расчета выглядит так:

a = b * ((1 — c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?

Как решаем: подставим в формулу данные из условий задачи.

100 * (1 – 25/100) = 75

75 выпускников закончат школу в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а * ((1 + у * х)/ 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?

Как решаем: подставим в формулу данные из условий задачи.

5000 * (1 + 12 * 15/100) = 14000

Родители через год внесут в банк 14000 рублей.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а * ((1 + х)/100)y,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.

Как решаем: просто подставим в формулу данные из условий задачи:

25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.

Способы нахождения процента

Универсальная формула для решения задач на проценты:

A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число.

Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.

Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.

Как считать проценты на калькуляторе: простейшие способы

Учитывая, что сегодня так называемые «счетные машинки» находятся на столе у любого школьника, продавца или бухгалтера, а также на любом телефоне и компьютере, нам не остается ничего другого, как считать проценты на калькуляторе. Мы не зря в начале статьи вспомнили школу и ваш дружный (а может и не дружный) шестой класс. Отбросив эти романтические переживания, перейдем к подсчету процентов.

Как вычислить процент от суммы: 1 способ

Давайте найдем необходимый процент с помощью простого примера. Допустим, вам необходимо найти 25% от суммы в 1000 рублей. Решаем следующий пример:

1000*25:100= 250

Как вычислить процент от суммы: 2 способ

Этот подсчет еще проще:

1000*0,25=250

Как вычислить процент от суммы: 3 способ

Ну и вычисление для совсем ленивых:

1000*25%=250

Вот вы и узнали простые способы, как посчитать проценты на калькуляторе. Мы уверены, что вы о них знали со школьной скамьи, и просто напомнили вам. Теперь вы можете применить эти знания и без проблем вычислить проценты по кредиту или по вкладу, самостоятельно подсчитав сумму процентов.

Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

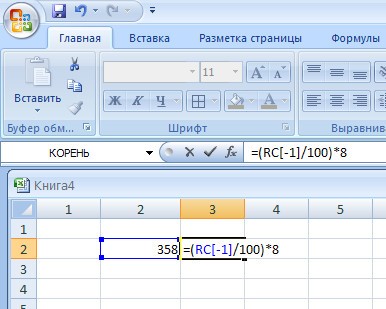
Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

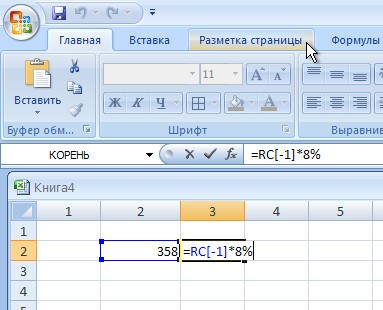
Иногда нам необходимо узнать процентный показатель от суммы.

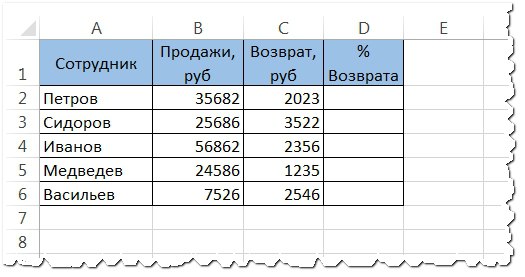
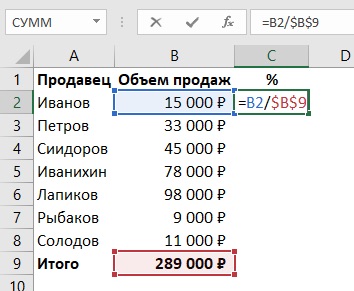
1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.

Видео: как посчитать проценты от суммы?

Быстрое вычисление процентов

Конечно, вычисление процентов при помощи пропорции является фундаментальным. Однако с применением дробных чисел это процедура упрощается до невозможности. Ведь что такое 50% на самом деле? Половина. То есть 1/2 или 0,5 (исходя из начального числа 1). Теперь понятно: чтобы вычислить половину, нужно умножить искомое число или на 1/2, или на 0,5 либо разделить на 2. Такой способ, правда, годится только для чисел, которые делятся без остатка.

В случае возникновения остатка или бесконечных знаков в периоде после запятой типа 0,33333333… лучше использовать дробные выражения наподобие 1/3. Кстати, именно дроби (в некоторых случаях иррациональные) со всей точностью отражают само число, ведь периодические цифры после запятой, сколько ни задавай, все равно целого числа не дадут. А так та же одна треть четко и понятно выражает саму суть.

В тех же рецептах, естественно, треть можно определить, так сказать, на глаз. А вот в химических процессах, особенно связанных с тонкой дозировкой компонентов, скажем, в фармацевтике, такой метод не подойдет. Здесь на глаз полагаться не приходится. Необходимо использовать точные соотношения ингредиентов, даже если один из показателей имеет вид числа с цифрой в периоде или представлен в виде той же иррациональной дроби. Но, как правило, к примеру при взвешивании, такие числа могут ограничиваться после запятой десятитысячными или максимум стотысячными.

Формулы расчета

Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.

Простой процент

Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.

Формула расчета:

S_N = S_П * (1 + % ст * N), где

• S_N – сумма в конце периода N;
• S_П – первоначальная сумма капитала;
• % ст – процентная ставка (доход);
• N – расчетный период.

Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.

В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.

В этом случае формула примет вид:

S_N = S_П * (1 + % ст * Д / 365), где

Д – количество полных дней нахождения денег на депозите.

Например:

1. Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
2. На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
3. На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.

Сложный процент с начислением дохода 1 раз в год

По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:

S_N = S_П * (1 + % ст)N

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.

Сложный процент с начислением дохода чаще, чем 1 раз в год

Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:

S_N = S_N * (1 + % ст / К)N*К, где

К – частота начисления дохода (12, 4 или 2 раза в год).

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.

Считаем процент от суммы вклада

Напомню, что проценты по банковскому вкладу могут быть простыми и сложными.

В первом случае банк начисляет доход на начальную сумму депозита. То есть, каждый месяц/квартал/год вкладчик получает от банка один и тот же «бонус».

Схема со сложными процентами для вкладчика выгоднее. Начисленный за месяц доход «плюсуется» к сумме вклада. И уже в следующем периоде процент будет насчитываться на большую сумму. А в следующем – на еще большую и так далее. На «длинных» сроках (10-20 лет) сложные проценты творят настоящие чудеса!

Конечно, формулы расчета для простых и сложных процентов отличаются друг от друга.

Рассмотрим их на конкретном примере.

Доходность по вкладу с простыми процентами

Сумма % = (вклад*ставка*дней в расчетном периоде)/(дней в году*100)

Пример. Валера открыл вклад на сумму 20 000 рублей под 9% годовых на один год.

Рассчитаем доходность вклада за год, месяц, неделю и один день.

Сумма процентов за год = (20 000*9*365)/(365*100) = 1800 рублей

Понятно, что в нашем примере годовую доходность можно было посчитать гораздо проще: 20 000*0,09. И в результате получить те же самые 1800 рублей. Но раз решили считать по формуле, то и будем считать по ней. Главное – понять логику.

Сумма процентов за месяц (июнь) = (20 000*9*30)/(365*100) = 148 рублей

Сумма процентов за неделю = (20 000*9*7)/(365*100) = 34,5 рублей

Сумма процентов за день = (20 000*9*1)/(365*100) = 5 рублей

Согласитесь, формула простых процентов элементарна. Она позволяет рассчитать доходность по вкладу за любое количество дней.

Доходность по вкладу со сложными процентами

Усложняем пример. Формула расчета сложных процентов уж чуть «мудреней», чем в предыдущем варианте. Калькулятор должен иметь функцию «степень». Как вариант, можно использовать опцию степень в таблице Excel.

• Сумма % = вклад*(1+ ставка за период капитализации)число капитализаций — вклад
• Ставка за период капитализации = (годовая ставка*дни в периоде капитализации)/(число дней в году*100)

Вернемся к нашему примеру. Валера разместил на банковском вкладе те же 20 000 рублей под 9% годовых. Но в этот раз — с ежемесячной капитализацией процентов.

Сначала посчитаем ставку за период капитализации. По условиям вклада проценты начисляются и «плюсуются» к депозиту один раз в месяц. Значит, в периоде капитализации у нас 30 дней.

Таким образом, ставка за период капитализации = (9*30)/(365*100) = 0,0074%

А теперь считаем, сколько наш вклад принесет в виде процентов за разные периоды.

Сумма процентов за год = 20 000*(1+0,0074) 12 – 20 000 = 1 850 рублей

В степень «12» мы возводим, потому что год включает двенадцать периодов капитализации.

Как видите, даже на такой символической сумме и коротком сроке разница в доходности вклада с простыми и сложными процентами составляет 50 рублей.

Сумма процентов за полгода = 20 000*(1+0,0074) 6 – 20 000 = 905 рублей

Сумма процентов за квартал = 20 000*(1+0,0074) 3 – 20 000 = 447 рублей

Сумма процентов за месяц = 20 000*(1+0,0074) 1 – 20 000 = 148 рублей

Вкладчик получит все те же 148 рублей и с простыми, и со сложными процентами. Расхождения в доходности начнутся со второго месяца. И чем длиннее срок депозита – тем существенней будет разница.

Пока мы не отошли далеко от темы сложных процентов, давайте проверим, насколько справедлива одна из рекомендаций финансовых консультантов. Я имею в виду совет выбирать вклады с капитализацией процентов не раз в полгода или квартал, а раз в месяц.

Предположим, наш условный Валера оформил депозит на ту же сумму, срок и под ту же ставку, но с капитализацией процентов раз в полгода.

Для начала нам придется пересчитать ставку за период капитализации. Ведь теперь этот период составляет не 30 дней (месяц), а 182 дня (полгода).

Ставка = (9*182)/(365*100) = 0,0449%

Теперь считаем доходность по вкладу за год.

Сумма процентов за год = 20 000*(1+0,0449) 2 – 20 000 = 1 836 рублей

Вывод: при прочих равных условиях полугодовая капитализация принесет Валере на 14 рублей меньше, чем ежемесячная (1850 – 1836).

Понимаю, что разница совсем невелика. Но ведь и другие исходные данные у нас символические. На крупных суммах и длинных сроках 14 рублей превратятся в тысячи и миллионы.

Сравнение величин в процентах

Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах. Если сравнение по разности вполне однозначно, то есть всегда можно найти, насколько одна величина больше или меньше другой, то для сравнения в процентах нужно указывать, относительно какой величины вычисляется процент. Такое указание, впрочем, необязательно в том случае, когда говорят, что одна величина больше другой на число процентов, превышающее 100. В этом случае остается только одна возможность вычисления процента, а именно деление разности на меньшее из двух чисел с последующим умножением результата на 100.

Что такое процент?

В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.

Процентом называется одна сотая часть чего-либо

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Как найти процентное соотношение чисел

Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.

Для определения такого результата существуют следующая формула:

B / A * 100 =

К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.

Используя приведённую формулу, выполняем несложные арифметические операции:

85 / 500 * 100 = 17%

Таким образом, число 85 составляет 17% от 500.

Проверяем полученное число по формуле первого способа:

500 / 100 * 17 = 85.

Всё сошлось.

Расчет при помощи онлайн-калькулятора

Вычислить процент при помощи обычного онлайн-калькулятора не представляет труда.

Многие из них сделаны по принципу стандартных устройств, а потому вычисления проходят по выше указанной схеме.

Если же на онлайн-калькуляторе нет кнопки «%», вычисления могут проходить двумя способами:

1. Необходимо разделить процент на 100 и умножить на данное число. Пример: выделить 15% от 300. 15/100 = 0,15; 0,15*300 = 45.
2. Разделить число на 100 и умножить на процент: 300/100 = 3; 3*15 = 45.

Если нахождение необходимо для оплаты кредита, ипотеки, ОСАГО или налоговых вычетов, можно воспользоваться специализированными калькуляторами. Их легко найти по поиску.

Они значительно отличаются от простых калькуляторов: например, при расчете стоимости ОСАГО потребуется выбрать тип автомобиля, мощность двигателя, указать стаж, возраст и область и некоторые другие данные. Исходя из этих данных, калькулятор сосчитает примерную среднюю стоимость в рублях полиса.

Стоит отметить: к сожалению, полученная при таких подсчетах сумма лишь примерна – правильные данные будут рассчитаны специалистом при личном обращении.

Как посчитать, сколько это процентов?

Этот вопрос задает каждый покупатель магазина, который намеревается воспользоваться акцией, и каждый сотрудник компании, желающий узнать размер своего вознаграждения за выполнение плана. Ведь проценты присутствуют во многих сферах повседневной жизни.

Возьмем конкретный пример. В магазине наушники стоили 3000 рублей, на них появилась акция в виде скидки 30%. Какая сумма вашей выгоды и сколько надо заплатить за товар?

Расчет простой

• 3000×30/100 = 900, поскольку 30/100 можно еще записать как 0,30, то
• 3000×0,30 = 900 рублей — это сумма скидки (30%) в денежном эквиваленте.

Теперь посчитаем сколько надо заплатить за наушники: 3000-900=2100 руб.

Расчет процентов — это не только задание на уроке в школе, но и актуальный вопрос для многих взрослых. Не у всех есть способность быстро выполнять действия в уме. Хотя рассчитать 10% или 20% от заданной суммы довольно просто, вычисление размера, например процентной ставки по банковским операциям иногда бывает проблематичным.

Что делать в этой ситуации? Вы можете прибегнуть к помощи специалиста, но проще применить свои навыки в использовании современных технологий и использовать онлайн калькулятор расчета процентов.

О легких и простых методах расчета процентов вы узнаете из видео.

Читайте далее:

Калькулятор автокредита: рассчитать процент переплаты

Онлайн конвертер долей, перевод дюжин, процентов, промилле и других единиц

Особенности ипотечного кредита: что нужно знать перед оформлением

Калькулятор сравнения шин, преимущества и недостатки изменения размера

Калькулятор расхода топлива, как рассчитать стоимость поездки

Как рассчитать доходность сделок по акциям, калькулятор расчета

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Как решаем:

76 : 100 = 0,76 — 1% от массы человека

0,76 * 70 = 53,2

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Как решаем:

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

х — 0,4х = 0,6x

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х — 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

х — 0,45x = 0,55х

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Ответ: 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

Как решаем:

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

100 — 8 = 92

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

92 : 4 = 23

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

23 * 5 = 115

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

Как решаем:

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Как решаем:

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.

19 : 0,1 = 190

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.