Обычный или инженерный калькулятор онлайн

Примеры

linur_i 5:2 3 10 2 -11:3 0:-30

Корни системы линейных уравнений равны следующим значениям.

Переменные считаются слева направо

1.4389598942265:-1.941383869546

-0.3591890700749:2.2763331864257

 то есть x1=1.4389598942265 — 1.941383869546 i 

x2=-0.3591890700749+2.2763331864257 i

Рассчитаем комплексную систему линейных уравнений

такого вида

Записываем все элементы в поле ввода. Как видите, данные могут быть не только числовые но и быть произвольным выражением, включающее в себя комплексные числа.

И получаем следующий результат.

Вы ввели следующую систему уравнений

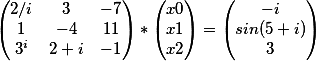Решение системы следующее

Успехов в расчетах !

• Скалярное произведение двух матриц >>

Формы, как записываются

Алгебраическая запись комплексного числа имеет такой вид:

z = a + bi.

Кроме данной формы существует еще несколько способов для записи. Удобным и наглядным геометрическим представлением является:

z = a + bi в виде вектора с координатами (а;b) на декартовой плоскости, либо точкой — концом вектора с аналогичными координатами.

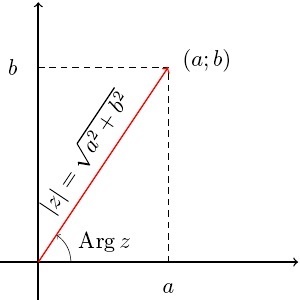
В этом случае пару комплексных чисел представляют в виде суммы соответствующих векторов, которую рассчитывают с помощью правила параллелограмма. Согласно теореме Пифагора, длина вектора с координатами (а;b) определяется, как:

\(\sqrt{a^{2}+b^{2}}\)

Данная величина представляет собой модуль комплексного числа z = a + bi и имеет такое решение:

\(\left|z \right|\)

Вектор и положительное направление оси абсцисс образуют угол, отсчитанный против часовой стрелки. Данный угол называют аргументом комплексного числа z и обозначают, как Arg z. Аргумент имеет неоднозначное определение с точностью до прибавления величины, которая кратна 2π радиан. При повороте на такой угол вокруг начала координат вектор не изменяется.

В том случае, когда вектор длиной r с положительным направлением оси абсцисс составляет угол ϕ, его координаты будут следующими:

\(\left(r*\cos \varphi ;r*\sin \varphi \right)\)

Таким образом, получают тригонометрическую форму записи комплексного числа:

\(z=\left|z \right|*\left(\cos (Arg z)+i\sin (Arg z) \right)\)

Из-за более простого вида вкладок комплексные числа, как правило, представляют в тригонометрической форме.

Существует показательная форма для записи комплексных чисел. Какое-либо комплексное число, не равное нулю, можно представить в показательной форме:

\(z=\left|z \right|*e^{i\varphi }\)

Где \(\left|z \right|\)является модулем комплексного числа,

\(\varphi\) представляет собой аргумент комплексного числа.

Представить комплексное число в показательной форме можно с помощью нескольких действий:

• изобразить чертеж;
• найти модуль;
• рассчитать аргумент.

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i
• деление:
  a + bi
  c + di
  =
  (a + bi)(c — di)
  c2 + d2
  =
  (ac + bd)
  c2 + d2
  +
  (bc — ad)
  c2 + d2
  i

Примеры

Найти сумму чисел и :
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом: + =

Найти разность чисел и :
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом: — =

Найти произведение чисел и :
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом: * =

Найти отношение чисел и :
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом: / =

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

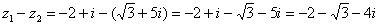
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность: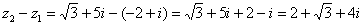
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно: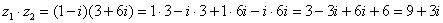

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно: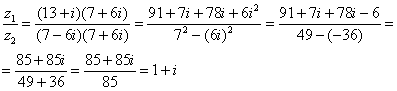

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :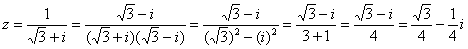

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Изображение комплексных чисел радиус-векторами координатной плоскости

      Рассмотрим плоскость с заданной на ней   Oxy   и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

      Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число   z = x + i y   радиус–вектором с координатами   (x , y).

      Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.

      При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Деление комплексных чисел:

$$\frac{x_1+iy_1}{x_2+iy_2}=\frac{(x_1+iy_1)(x_2-iy_2)}{(x_2+iy_2)(x_2-iy_2)}=\frac{x_1x_2+y_1y_2+i(y_1x_2-x_1y_2)}{x_2^2+y_2^2}=$$ $$\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+\frac{y_1x_2-x_1y_2}{x_2^2+y_2^2}i.$$

Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$

Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$

Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$

Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.

Примеры:

Выполнить действия над комплексными числами, представив результат в алгебраичекой  форме: 

1.421.  $(2+3i)(3-i).$

Решение:

$(2+3i)(3-i)=6-2i+9i-3i^2=6+7i+3=9+7i.$

Ответ: $9+7i.$

1.424. $(2i-i^2)^2+(1-3i)^3.$

Решение.

$(2i-i^2)^2+(1-3i)^3=(2i+1)^2+1-3(3i)^2+3(3i)-(3i)^3=$ $=4i^2+4i+1-27i^2+9i-27i^3=-4+4i+1+27-9i+27i=24+22i.$

Ответ: $24+22i.$

1.425. $\frac{2-i}{1+i}.$

Решение.

$$\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{2-2i-i+i^2}{1-i^2}=\frac{2-3i-1}{1+1}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i.$$

Ответ: $\frac{1}{2}-\frac{3}{2}i.$

 {jumi}

1.428. $\frac{(1+i)(3+i)}{3-i}-\frac{(1-i)(3-i)}{3+i}.$

Решение.

$$\frac{(1+i)(3+i)}{3-i}-\frac{(1-i)(3-i)}{3+i}=\frac{(1+i)(3+i)(3+i)}{(3-i)(3+i)}-$$ $$-\frac{(1-i)(3-i)(3-i)}{(3+i)(3-i)}=\frac{9+15i+7i^2+i^3}{9-i^2}-\frac{9-15i+7i^2-i^3}{9-i^2}=$$ $$=\frac{9+15i-7-i-9+15i+7-i}{10}=\frac{28}{10}i=\frac{14}{5}i.$$

Ответ: $\frac{14}{5}i.$

Найти действительные решения следующего уравнения:

1. 430. $(1+i)x+(-2+5i)y=-4+17i.$

Решение.

$(1+i)x+(-2+5i)y=-4+17i\Rightarrow$

$x+xi-2y+5yi=-4+17i\Rightarrow$

$(x-2y)+(x+5y)i=-4+17i\Rightarrow$

$$\left\{\begin{array}{lcl}x-2y=-4\\x+5y=17\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2y-4\\2y-4+5y=17\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2\\y=3\end{array}\right. .$$

Ответ: $x=2; y=3.$

Домашнее задание.

Выполнить действия над комплексными числами, представив результат в алгебраичекой  форме: 

1.422.  $(1+2i)^2.$

Ответ: $-3+4i.$

1.423. $(1-i)^3-(1+i)^3.$

Ответ: $-4i.$

1.426. $\frac{1}{1+4i}+\frac{1}{4-i}.$

Ответ: $\frac{5}{17}-\frac{3}{17}i.$

1.427. $\left(\frac{1-i}{1+i}\right)^3.$

Ответ: $i.$

 Найти действительные решения следующего уравнения:

1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$

Ответ: $x=1/3; y=1/4.$

Решить следующие системы линейных уравнений:

1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$

           $(4+2i)z_1-(2+3i)z_2=7.$

Ответ: $z_1=1; z_2=i.$

1.433. $(2+i)z_1+(2-i)z_2=6;$

           $(3+2i)z_1+(3-2i)z_2=8.$

Ответ: $z_1=2+i; z_2=2-i.$

Алгоритм решения комплексных уравнений вида z^n-a=0

1. Найти модуль и аргумент числа .2. Записать формулу (1.17) при заданном значении .3. Выписать значения корней уравнения , придавая значения .

Пример 1.24. Решить уравнения: a) ; б) .

Решение

Задача равносильна задаче нахождения всех значений корня из комплексного числа. Решаем в каждом случае по алгоритму.

а) Найдем .1. Определим модуль и аргумент числа .2. При полученных значениях и записываем формулу (1.17):

Заметим, что справа стоит — арифметический корень, его единственное значение равно 1.

3. Придавая последовательно значения от 0 до 5, выписываем решения уравнения:

Геометрически соответствующие точки расположены в вершинах правильного шестиугольника, вписанного в окружность радиуса , одна из точек (соответствует ) . Строим шестиугольник (рис. 1.8,в). Отметим свойства корней этого уравнения с действительными коэффициентами — его комплексные корни являются попарно сопряженными: и — действительные числа.

б) Найдем .1. Определим модуль и аргумент числа .2. По формуле (1.17) имеем

3. Выписываем корни .

Для геометрического представления решения уравнения достаточно изобразить одно значение, например (при ) — это точка окружности , лежащая на луче . После этого строим правильный треугольник, вписанный в окружность (рис. 1.8,б).

Пример 1.25. Найти корень уравнения , для которого .

Решение

Задача равносильна задаче нахождения при условие .

1. Находим модуль и аргумент числа .

2. По формуле (1.17) имеем: .

3. Для нахождения искомого решения нет необходимости выписывать все значения корня. Нужно выбрать значение , при котором выполняется условие (соответствующая точка — точка второй четверти). Удобно при этом использовать чертеж (рис. 1.9).

Условию поставленной задачи удовлетворяет корень (при ): .

(помощь с решением задач, обсуждение вопросов по математике).

Деление комплексных чисел

Как и при любом делении в алгебре, комплексное число нельзя делить на нуль
и на комплексное число .

При делении комплексного числа на действительное число на это число нужно
разделить и действительную, и мнимую компоненты. При делении комплексного числа на
комплексное число нужно делимое и делитель умножить на число, сопряжённое делителю.

Пример 9. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Автор проекта был свидетелем вопроса о том, откуда взялось 5 в знаменателе дроби.
Пояснения вызывают реакцию «А слона-то я и не заметил!». Пояснения следующие: не забываем, что мы
имеем дело с комплексными числами и знаем, что — это
не какая-нибудь переменная, а корень из минус единицы. Таким образом,

.

Пример 10. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Если всё же возникает вопрос, откуда в знаменателе дроби 10, смотрите пояснения в
конце предыдущего примера.

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (, , ), десятичные дроби (, , ), а также числа в экспоненциальной форме (, ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (, , , ) для перемещения по элементам

Аргумент комплексного числа

Полярный угол точки называется аргументом комплексного числа . Обозначение: .

В дальнейшем, если нет специальных оговорок, под будем понимать значение , удовлетворяющее условию . Так, для точки (см. рис. 1.1) .

Формулу для нахождения аргумента комплексного числа , заданного в алгебраической форме, получаем, используя связь декартовых и полярных координат точки (см. рис. 1.3,б). Для точек, не лежащих на мнимой оси, т.е. для , у которых , получаем ; для точек мнимой положительной полуоси, т.е. для , у которых , имеем ; для точек мнимой отрицательной полуоси, т.е. для , у которых , соответственно .

Аргумент числа — величина неопределенная.

Нахождение аргумента при сводится к решению тригонометрического уравнения . При , т.е. когда — число действительное, имеем при и при . При решение уравнения зависит от четверти плоскости . Четверть, в которое расположена точка , определяется по знакам и . В результате получаем:

(1.6)

При решении примеров удобно пользоваться схемой, которая изображена на рис. 1.5.

Пример 1.14. Найти аргументы чисел из примера 1.13.

Решение

Как и в примере 1.13, решим задачу для каждого из трех случаев:

1) числа и — действительные, причем , поэтому (см. рис. 1.4);

2) числа и — чисто мнимые , причем , поэтому (см. рис. 1.4);

3) для числа имеем , поэтому из находим ; так как при этом (точка находится во второй четверти, рис. 1.4), то получаем (рис. 1.5) или .

Пример 1.15. Найти модуль и аргумент числа .

Решение. Находим . Так как , т.е. точка расположена в четвертой четверти, то из равенства получаем (рис. 1.5).

Перевод чисел из одной системы счисления в другую

Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:

1. Перевести число в десятичную систему счисления.Решение: = = = Ответ: =

2. Перевести число в десятичную систему счисления.Решение: = = = Ответ: =

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.

Перевод целой части числа из десятичной системы счисления в другую систему счисления

Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.

3. Перевести число в восьмиричную систему счисления.Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421Проверка: = = = , результат совпал. Значит перевод выполнен правильно.Ответ: =

Рассмотрим перевод правильных десятичных дробей в различные системы счисления.

Перевод дробной части числа из десятичной системы счисления в другую систему счисления

Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.

4. Перевести число в двоичную систему счисления.Решение: (0 — целая часть, которая станет первой цифрой результата), (0 — вторая цифра результата), (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).Ответ: =

Извлечение корня натуральной степени из комплексного числа

      Пусть — произвольное комплексное число, отличное от нуля.

      Корнем   n — ой степени из числа  z , где  называют такое комплексное число   z = r e iφ , которое является решением уравнения

z n = z .

(8)

      Для того, чтобы решить уравнение (8), перепишем его в виде

и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна   2kπ ,   где   k   — произвольное целое число. По этой причине справедливы равенства

следствием которых являются равенства

(9)

      Из формул (9) вытекает, что уравнение (8) имеет   n   различных корней

(10)

где

причем на комплексной плоскости концы радиус-векторов   z_k   при   k = 0 , … , n – 1   располагаются в вершинах правильного   n — угольника, вписанного в окружность радиуса  с центром в начале координат.

      Замечание. В случае   n = 2   уравнение (8) имеет два различных корня   z₁   и   z₂ , отличающихся знаком:

z₂ = – z₁ .

      Пример 1. Найти все корни уравнения

z3 = – 8i .

      Решение. Поскольку

то по формуле (10) получаем:

      Следовательно,

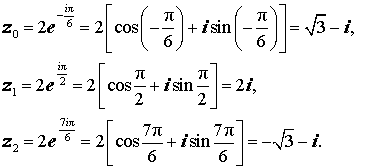
      Пример 2. Решить уравнение

z2 + 2z + 2 = 0 .

      Решение. Поскольку отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:

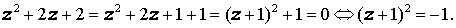
      Так как

то решения уравнения имеют вид

z₁ = – 1 + i ,       z₂ = – 1 – i .

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

      Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

      Действительно, умножение и деление двух произвольных комплексных чисел  и  записанных в экспоненциальной форме, осуществляется по формулам

      Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

      При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

      Возведение комплексного числа   z = r e iφ в натуральную степень осуществляется по формуле

      Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Возведение в степень комплексного числа в тригонометрической форме

Из определения степени и правила умножения чисел, записанных в тригонометрической форме (формула (1.10)), получаем

, где .

Правило возведения в степень. При возведении в степень комплексного числа в эту степень возводится модуль числа, а аргумент умножается на показатель степени:

(1.12)

Записывая число в тригонометрической форме , получаем формулу возведения в степень:

(1.13)

При это равенство принимает вид и называется формула Муавра

(1.14)

Пример 1.21. Найти модуль и аргумент комплексного числа .

Решение. Обозначим . Находим модуль и аргумент числа . Поэтому и . Так как по определению для главного значения аргумента выполняется условие , то .

Пример 1.22. Записать в тригонометрической форме число .

Решение

Обозначим . Находим модули и аргументы чисел и . Для числа имеем: (см. пример 1.21). Для числа последовательно находим: (см. пример 1.19), , или, находя главное значение аргумента: . Таким образом, по формуле (1.10) получаем

и

Записываем число в тригонометрической форме:

Пример 1.23. Используя формулу Муавра, найти выражения для и через тригонометрические функции угла .

Решение

Из формулы (1.14) при имеем . Возведем левую часть в степень, учитывая, что (см. пример 1.8):

Используя условие равенства комплексных чисел, получаем:

Тригонометрическая форма комплексного числа

Каждому комплексному числу геометрически соответствует точка на плоскости . Но положение точки на плоскости, кроме декартовых координат , можно зафиксировать другой парой — ее полярных координат в полярной системе (рис. 1.3,a).

Величина является неотрицательной и для данной точки определяется единственным образом, а угол может принимать бесчисленное множество значений (при этом ): если точке соответствует некоторое значение , то ей также соответствуют значения . Например, если для точки (см. рис. 1.1) выбрать , то ей соответствует любое , в частности при . Если же выбрать , то , а при получаем .

Используя связь декартовых и полярных координат точки (рис. 1.3,б), из алгебраической формы записи комплексного числа получаем тригонометрическую форму:

(1.3)

Алгебраическая форма записи комплексных чисел

      Пусть x и y — произвольные вещественные числа.

      Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

      Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0).

      Комплексные числа, заданные парами (0, y), называют чисто мнимыми числами.

      Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.

      Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число   z, заданное парой вещественных чисел   (x, y), записывается в виде

z = x + i y .

(1)

где использован символ   i , называемый мнимой единицей.

      Число x называют вещественной (реальной) частью комплексного числа   z = x + i y   и обозначают   Re z.

      Число y называют мнимой частью комплексного числа   z = x + i y   и обозначают   Im z.

      Комплексные числа, у которых   Im z = 0 , являются вещественными числами.

      Комплексные числа, у которых     Re z = 0 , являются чисто мнимыми числами.

      Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Извлечение корня из комплексного числа в тригонометрической форме

Рассмотрим задачу извлечения корня из комплексного числа, заданного в показательной или тригонометрической форме , или . Искомое число также запишем в показательной форме: . Используя определение операции извлечения корня и условия (1.8), получаем соотношения

или

(1.15)

Правило извлечения корня. Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент разделить на показатель корня:

(1.16)

Теперь можно записать число в показательной форме:

Если записать это соотношение в тригонометрической форме, то, учитывая периодичность тригонометрических функций, нетрудно убедиться, что выражение принимает только различных значений. Для их записи достаточно в формуле (1.15) взять последовательных значений , например . В результате получаем формулу извлечения корня из комплексного числа в тригонометрической форме, где :

(1.17)

Замечания 1.1

1. Рассмотренная задача извлечения корня степени из комплексного числа равносильна решению уравнения вида , где, очевидно, .

Для решения уравнения нужно найти значений , а для этого необходимо найти и использовать формулу извлечения корня.

2. Исследование формулы (1.17) показывает, что все комплексные числа (значения ) имеют равные модули, т.е. геометрически расположены на окружности радиуса . Аргументы двух последовательных чисел отличаются на , так как , т.е. каждое последующее значение может быть получено из предыдущего поворотом радиуса-вектора точки на .В этом заключается геометрический смысл формулы (1.17), что можно сформулировать следующим образом.

Точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой , причем аргумент одного из значений равен (рис. 1.7).

Линейная алгебра

1. Определитель матрицы.
2. Матричный калькулятор:
3. Методы решения системы уравнений: метод Гаусса, метод Крамера, метод обратной матрицы и другие.
4. Координаты вектора в новом базисе. Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
5. Приведение кривой второго порядка к каноническому виду
6. Собственные числа матрицы
7. Выделение полного квадрата (a•x2 + b•x + c = 0)
8. Метод неопределенных коэффициентов (преобразовать в сумму простейших дробей):
9. Формула дискриминанта. Данный вид калькулятора используется для нахождения дискриминанта и корней функции.
10. Деление многочленов столбиком. Данная процедура, в частности, поможет при нахождении интегралов.
11. Решение пределов.
12. Точки разрыва функции.

Раскрыть скобки и упростить выражение, (x2/3 — 3x + 12)(x + 2)

Комплексная плоскость

Из определения комплексного числа как упорядоченной пары действительных чисел (см. введение) получаем, что задание комплексного числа можно рассматривать как задание точки на плоскости, абсциссой которой является , ординатой , т.е. числу соответствует точка . Между множеством точек плоскости и множеством комплексных чисел (множество ) устанавливается взаимно однозначное соответствие: каждой точке соответствует единственное число , каждому числу соответствует единственная точка с координатами ; плоскость при этом называется комплексной плоскостью (плоскость ). На рис. 1.1 отмечены точки, соответствующие комплексным числам из примера 1.2.

Используя геометрическую интерпретацию комплексных чисел как точек плоскости, убеждаемся в справедливости утверждения, что комплексные числа не сравниваются, т.е. на множестве не определены операции сравнения (не имени места знаки ). Это следует из того, что множество точек плоскости не упорядочено.

Возведение комплексного числа в степень

Возведение комплексного числа в степень — это нахождение произведения сомножителей, каждый из которых равен , т.е. .

Правило возведения в степень. При возведении в степень числа (нахождении и ) используется правило возведения в степень двучлена , в общем случае применяется формула бинома Ньютона:

, где .

Пример 1.8. Найти различные степени числа , то есть .

Решение. Имеем . Замечая закономерность, получаем для следующие значения:

Пример 1.9. Найти мнимую и вещественную части комплексных чисел: .

Решение.

Пример 1.10. Возвести комплексное число в пятую степень.

Решение. Используем формулу бинома Ньютона при

Понятие бесконечности на множестве комплексных чисел

Как и в действительной области, на множестве комплексных чисел вводится понятие бесконечности, бесконечно удаленной точки. Это можно сделать по аналогии с множеством действительных чисел из геометрических соображений.

Рассмотрим числовую прямую и окружность , которая касается прямой в точке ; точку, диаметрально противоположную точке , обозначим (рис. 1.2,б).

Будем соединять прямыми различные точки оси с точкой ; точки пересечения прямых с окружностью будем обозначать . Очевидно, каждой точке соответствует точка . Обратное справедливо для всех точек окружности, за исключением точки . Но по мере удаления по прямой от точки (с увеличением расстояния, равного ), ее образ на окружности приближается к точке . Для последовательности такого вида в анализе принято название бесконечно большая последовательность (величина). Ее предел обозначается и называется бесконечностью или бесконечно удаленной точкой. Поэтому точку можно рассматривать как образ бесконечно удаленной точки на окружности, а бесконечность — как «точку» оси , образом которой на окружности является точка .

По аналогии рассмотрим плоскость (плоскость ) и сферу , касающуюся ее в начале координат, т.е. в точке (рис. 1.2,а). Лучи, соединяющие точки с точкой пересекают сферу в точках . При этом любой точке соответствует единственная точка , и наоборот, любой точке соответствует единственная точка . Очевидно, чем дальше расположена точка от начала координат ( — длина радиуса-вектора точки ), тем ближе ее образ к точке . Чтобы соответствие было полным, вводится «несобственный» элемент (символ ) , бесконечно удаленная точка как точка плоскости, образом которой на является точка .

Плоскость , дополненная элементом , называется расширенной комплексной плоскостью и обозначается .

Построенное взаимно однозначное соответствие точек сферы и множества называется стереографической проекцией, а сфера — сферой Римана.

Умножение комплексных чисел

Умножение комплексных чисел немного сложнее и заставляет задуматься:

А что значит перемножить два комплексных числа?

Самый простой способ понять мнимые числа — это интерпретировать умножение +1, -1 и √-1 (или, как Гаусс говорит прямые, обратные и боковые единицы) как вращение вокруг комплексной плоскости против часовой стрелки.

Умножение на +1

Умножение на +1 можно представить как вращение на 0˚ или 360˚ относительно начала координат, поскольку в любом случае вы вернетесь туда, откуда начали.

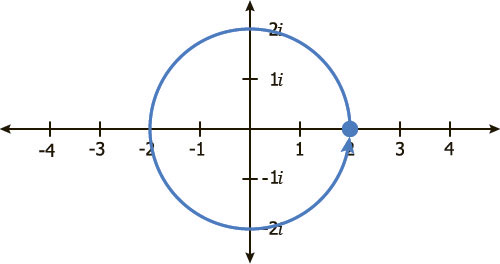Умножение на +1

Умножение на -1

Умножение на -1 можно интерпретировать как вращение на 180˚ против часовой стрелки вокруг начала координат. Например, если я начинаю с 2 и умножаю на -1, Я заканчиваю на -2, что составляет 180˚ против часовой стрелки. И если я умножу -2 на -1, я вернусь к положительному 2.

Умножение на i или √-1

А теперь самое интересное.

Умножая на i или √-1 мы поворачиваем плоскость на 90˚. Вот здесь мнимые числа и вступают в игру.

Обратите внимание, что если я умножу 2 на i, я получу 2i, что является поворотом на 90˚

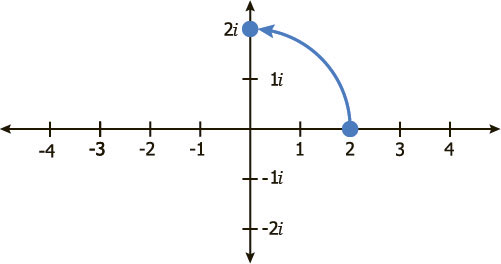
Если я умножу 2i на i, я получу 2i², что есть -2, так как i² фактически равно -1.

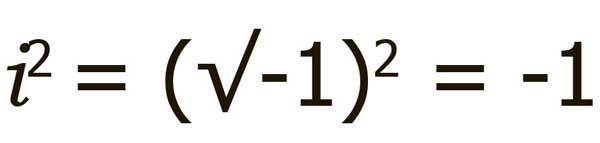
Итак, 2i ² = 2 (-1) или -2, еще 90° против часовой стрелки.

Умножение на i или √-1

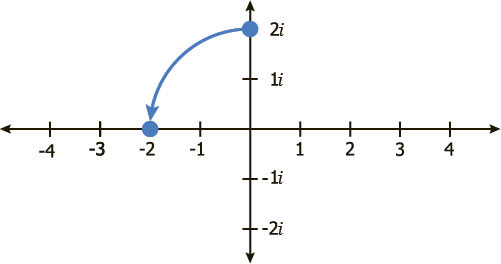
Точно так же, -2 умноженное на i равно -2i, еще четверть оборота.

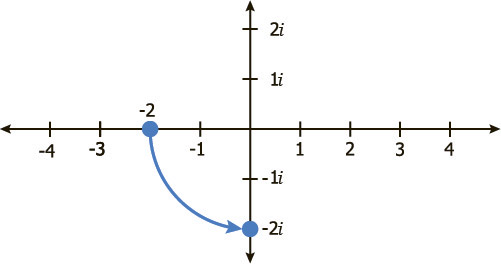
И наконец, -2i умноженное на i равно -2i² или -2(-1) что равно 2.

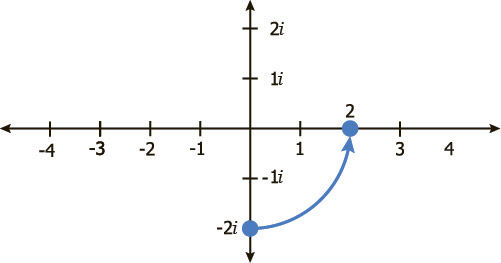
Мы могли бы продолжать умножать на i и вращаться вокруг плоскости, поэтому данный пример даёт нам шаблон, который повторяется каждые 4 цикла.

В общем, мы знаем, что
умножение на действительное число масштабирует значение, и мы чуть выше узнали,
что умножение на i поворачивает значение на 90° против часовой
стрелки, но как насчет этого?

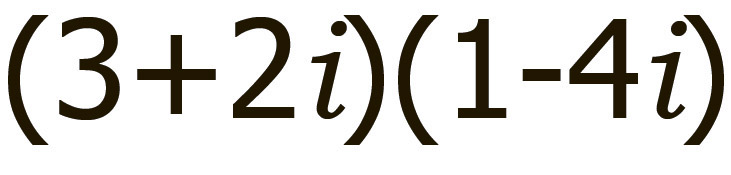
Чтобы лучше понять, давайте распишем.

Хорошо, теперь мы можем выполнить сложение векторов. Первый вектор это (3+2i) (1), как мы рассмотрели выше (3+2i) поворачивается на 360˚, то есть остается на месте.

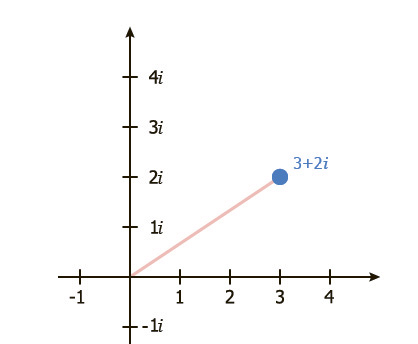
Теперь мы рассмотрим второй вектор (3 + 2i) (- 4i). Здесь происходит то же самое, что и с первым вектором: масштабирование и вращение. Вот как это происходит.

Сначала вектор (3 + 2i) умножаем на 4, и получаем (12 + 8i), этим мы растянули вектор (3 + 2i) в 4 раза.

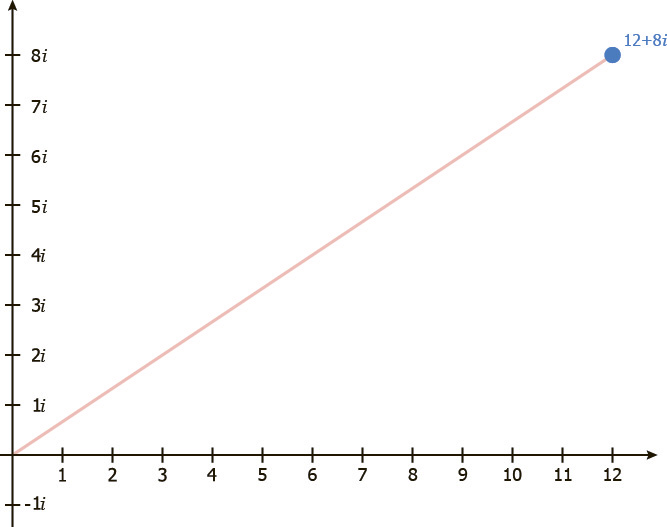
Нам также нужно умножить на -i. Напомним, умножая на -i мы поворачиваем на 90˚ по часовой стрелке.

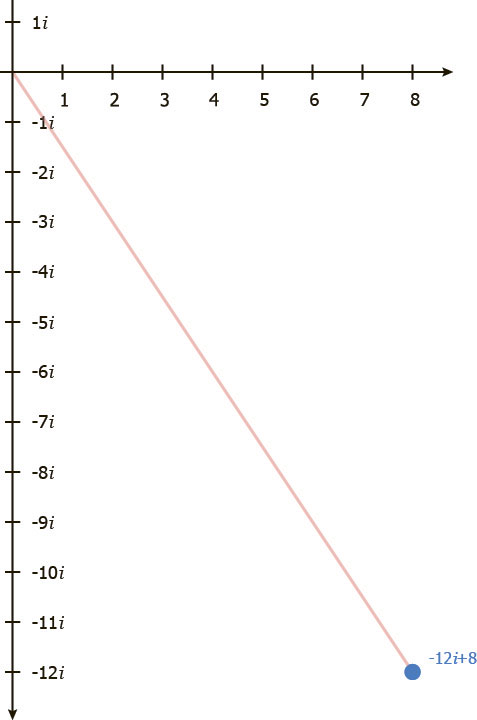
Теперь распишем полученное с помощью алгебры.

Последний шар — выполним сложение, перенеся параллельно начало одного вектора в конец другого.

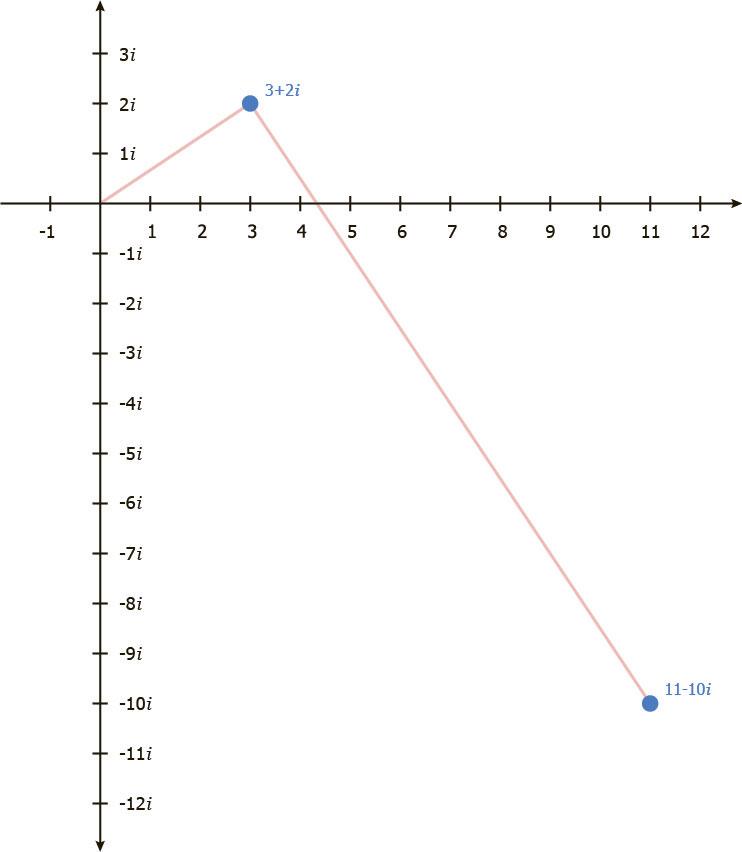
Наш окончательный ответ 11 — 10i.

Теперь у вас может возникнуть вопрос, почему мы не можем просто решить все с помощью алгебры?

И это так, мы можем решить это с помощью алгебры. На самом деле, это самый эффективный способ решения задачи (хотя ему не хватает понимания, которое вы получаете от построения графиков). Поэтому мы предложили вашему вниманию оба пути решения.

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа:
• Получение мнимой части числа:
• Модуль числа:
• Аргумент числа:
• Экспонента:
• Логарифм:
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(42 + (-3)2) = √25 = 5