Сколько арабских цифр существует на сегодняшний день. история появления

Использование нуля в расчетах

Детей в школе учат начинать отсчет с единицы. Но большинство программистов используют вычисления, где отсчет всегда начинается с нуля. Такая запись всех 10 чисел удобна тем, что для их представления используется только 1 символ. А экономия в программировании является неотъемлемой его частью. Если мы начнем отсчет с нуля, записывать цифру 10 нам не нужно. Её место занимает девятка.

Ноль обладает другими интересными свойствами при взаимодействии с числами. Так, если вы попытаетесь прибавить к нулю или отнять ноль от какого-нибудь числа — оно не изменится. Когда производится умножение на это число — вы получите 0 во всех случаях. При возведении каждого числа в ноль, получится единица. А также на ноль (0) нельзя разделить другое целое или дробное число.

Существует Закон Бенфорда . Если не вдаваться в подробности с рассмотрением формул и таблиц, он гласит, что в реальной жизни цифры от 1 до 4 встретить гораздо вероятнее, чем цифры от 5 до 9 . Сюда можно отнести номера домов улиц, различную статистику и тому подобное. Есть у этого закона и практическое применение. Используя его, можно проверять бухгалтерские отчетности, результаты голосований, подсчет расходов.

В некоторых американских штатах несоответствие каких-либо расчетов по Закону Бенфорда является уликой, имеющей вес в судебном процессе. Все расчеты по этому закону производятся в десятичной системе. Таким образом, арабские цифры в диапазоне от 1 до 10 являются самыми распространенными во всем мире.

Источник статьи: http://it-doc.info/arabskie-cifry-ot-1-do-10/

Новая, или арабская нумерация

Это, самая распространенная на сегодняшний
день нумерация. Название «арабская»
для нее не совсем верно, поскольку хоть
и завезли ее в Европу из арабских стран,
но там она тоже была не родной. Настоящая
родина этой нумерации — Индия.

В различных районах Индии существовали
разнообразные системы нумерации, но в
какой-то момент среди них выделилась
одна. В ней цифры имели вид начальных
букв соответствующих числительных на
древнеиндийском языке — санскрите,
использующем алфавит «Деванагари».

1

2

3

4

5

6

7

8

9

Первоначально этими знаками представлялись
числа 1, 2, 3, … 9, 10, 20, 30, …, 90, 100, 1000; с их
помощью записывались другие числа. Но
в последствии был введен особый знак —
жирная точка, или кружок, для указания
пустующего разряда; и нумерация
«Деванагари» превратилась в
поместную десятичную систему. Как и
когда совершился такой переход — до сих
пор неизвестно. К середине VIII века
позиционная система нумерации получает
широкое применение. В это же время она
проникает в соседние страны: Индокитай,
Китай, Тибет, Среднюю Азию.

Решающую роль в распространении индийской
нумерации в арабских странах сыграло
руководство, составленное в начале IX
века Мухаммедом Аль Хорезми. Оно было
переведено в Западной Европе на латинский
язык в XII веке. В XIII веке индийская
нумерация получает преобладание в
Италии. В других странах она распространяется
к XVI веку. Европейцы, заимствовав нумерацию
у арабов, называли ее «арабской».
Это исторически неправильное название
удерживается и поныне.

Из арабского языка заимствовано и слово
«цифра» (по-арабски «сыфр»),
означающее буквально «пустое место»
(перевод санскритского слова «сунья»,
имеющего тот же смысл). Это слово
применялось для названия знака пустого
разряда, и этот смысл сохраняло до XVIII
века, хотя еще в XV веке появился латинский
термин «нуль» (nullum — ничто).

Форма индийских цифр претерпевала
многообразные изменения. Та форма,
которой мы сейчас пользуемся установилась
в XVI веке.

Как изображали числа в древности

Как будем проверять? А давайте посмотрим, как в старину (глубокую, очень глубокую) записывали числа. Давайте откроем старые тексты, где, по идее, должны быть цифры. Где будем смотреть? А давайте в старых библейских и коранических рукописях и для для интереса на древнеславянском, арабском и древнееврейском. Удивительно, везде цифры изображаются первыми девятью буквами соответствующих алфавитов. Интересно, а какой самый древний алфавит? . А кто правопреемник? . А какой язык был беспрерывным с тех пор? . А давайте сравним каждую из девяти современных цифр с первыми девятью буквами финикийского, древнееврейского и (для чистоты эксперимента) арабского алфавитов.

Дом мудрости и греческий перевод

Первоначально европейцы эпохи Средневековья приписывали эту цифровую систему полностью арабам, хотя мы теперь знаем, что это далеко не так. Причина этого скрывается в том, что европейским ученым и историкам казалось, что они происходят из конкретного источника — Дома мудрости в Багдаде.

Этот центр обучения был создан правителем аль-Мамуном в восьмом веке нашей эры и был сопоставим с великими центрами обучения в Александрии в Древней Греции.

Более того, эта школа была связана с переводом математических и философских текстов, которые были доступны на других языках того времени. Среди переводимых текстов были великие работы индийского математика Брахмагупта и тексты таких знаменитых греческих мыслителей, как Аристотель и Евклид.

Перевод сочинений Евклида, написанных около 300 г. до н. э., был особенно важен для современной математики. Некоторые из его текстов, как, например, «Отдел фигур», не сохранились в оригинальном греческом языке. Так, если бы не тогдашнее багдадское переводческое движение, мы могли бы утратить важнейшие математические работы.

Важнейшей из работ Евклида была книга «Элементы», которую сегодня можно считать самым важным математическим учебником, который когда-либо составлялся. В ней автор четко изложил все самые сложные математические идеи тех времен, именно это обеспечило долговечность его работы.

Нумерация страниц в разных версиях Ворда

В разных релизах программы доступ к панели «Номера страниц» расположен в разных пунктах меню.

В Word 2003 создание номеров страниц осуществляется через пункт «Вставка», подпункт «Номера страниц…».

В окне настроек можно выбрать расположение номера (верху, книзу), выравнивание (слева, по центру, справа) и наличие нумерации на первой странице.

Римские, арабские цифры и буквы настраиваются через «Формат».

Чтобы изменения вступили в силу жмем ОК.

Пронумеровать страницы в Ворде 2007 можно через пункт «Вставка» – «Номер страницы».

Иначе реализована эта возможность в Ворде 2013. На вкладке «Макет» выбираем «Разрыв» – «Следующая страница».

На следующем листе нужно выбрать колонтитул, в котором будет отображен номер (верхний / нижний). На вкладке «Конструктор» переходим в разделе «Работа с колонтитулами» и щелкам «Как в предыдущем разделе», чтобы разделить колонтитулы.

В поле «Колонтитул» выбираем «Номер страницы».

Вот как открыть окно настроек в разных версиях Ворда.

Нестандартные решения

Иногда возникает потребность выборочно пронумеровать листы. Например, в презентацию нужно вставить график, буклет или таблицу и на это странице не должно быть номера. Эта настройки также можно реализовать в Ворде и состоят из комбинации описанных ранее вариантов.

Сначала удаляем нумерацию на тех страницах, где она не должна присутствовать: «Вставка» – «Номер страницы» – «Удалить номера страниц».

Щелкаем в начало той страницы, где должна отобразиться нумерация. Если нужно пропустить две страницы в тексте, то курсов устанавливаем в начало третьего листа.

Вставляем разрыв на следующую страницу.

Щелкаем два раза по месту, где должен стоять номер, чтобы появилась надпись колонтитула.

Нажимаем кнопку «Как в предыдущем разделе» на вкладке «Колонтитул». Она должна поменять цвет с оранжевого на серый. Галочку «Особый колонтитул для первой страницы» убираем.

А теперь добавляем номер страницы.

Арабские цифры.

Арабские цифры

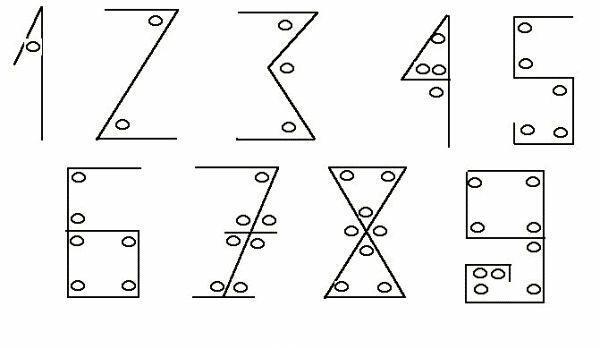
В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.

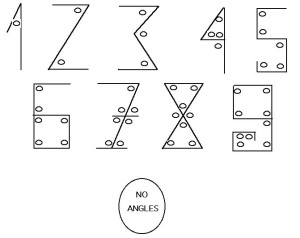
Запись цифры по числу углов

Далее произошло интересное: арабы переняли индийскую систему счисления и начали вовсю применять ее. В те времена мусульманский мир был очень развит, он имел очень тесные связи и с азиатской и европейской культурой и брал от них все самое совершенное и передовое на то время.

Математик Мухаммед Аль-Хорезми в IX веке составил руководство об индийской нумерации. Оно в XII веке попало в Европу и эта система счисления получило очень широкое распространение. Интересно, но именно из-за того, что к нам эти цифры пришли от арабов, мы их называем арабскими, а не индийскими.

Кстати, и само слово «цифра» — арабского происхождения. Арабы перевели индийское «сунья» и получилось «цифр».

Арабская система счисления называется позиционной. Это значит, что значение числа зависит от положения его в записи. То есть в числе 18 цифра 8 обозначает 8 единиц, а в числе 87 та же восьмерка обозначает 8 десятков. Позиционные системы наиболее совершенны. Но они произошли от непозиционных систем (которые, в принципе, существуют и сейчас) в результате развития человечества, его знаний и потребностей.

Интересно то, что современные арабские цифры сильно отличаются от тех, которые используем мы:

Современные арабские цифры

Вот такая история чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире.

Вам также может быть интересно:

Арабская система счисления

Замечание 1

Используемые в настоящее время цифры мы называем арабскими. Под арабскими цифрами понимается десяток математических символов, с помощью которых возможно записать любое число. Напомним эти общеизвестные символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Данные цифровые символы пришли в Европу в период примерно с десятого по тринадцатый век. На сегодняшний день, практически во всех странах применяются арабские цифры для записи чисел в десятичной системе счисления. Доказано, что основа арабских цифр появилась в Индии. Арабские цифры представляют собой видоизменённые индийские цифры. В средние века жил учёный Мухаммед ибн Муса аль-Хорезми, который занимался математикой, астрономией, другими науками, и который сформировал Индийскую систему написания чисел и сделал её очень популярной. Он написал трактат «Китаб аль-джебр ва-аль-мукабала», от названия которого затем появился термин «алгебра». Впоследствии этот термин вырос в название целой науки, которая и сегодня занимает достойное место в ряду научных дисциплин.

Основные правила осуществления арифметических операций над целыми числами и простыми дробями в десятичной системе счисления первым сформулировал именно выдающийся средневековый учёный Мухаммед ибн Муса аль-Хорезми, имя которого в переводе означает «Мухаммед, сын Мусы из Хорезма». Аль-Хорезми сделал все свои открытия в девятом веке нашей эры. Но оригинал его работ по основам арифметики на арабском был потерян, хотя остался перевод на латынь двенадцатого века. На основании этого текста Западная Европа получила десятичную позиционную систему счисления и правила осуществления в этой системе основных арифметических операций. Аль-Хорезми хотел добиться того, чтобы выработанные и прописанные им правила понимали все грамотные люди. Но в то время было очень много сложностей, таких как отсутствие чёткой математической символики типа знаков операций, скобок, символьных обозначений и тому подобное. Тем не менее, Аль-Хорезми сумел сформировать в своих работах такой формат ясных, строго очерченных словесных описаний, который не позволял читателю увидеть никаких двояких толкований или неправильно выполнить какие-либо операции.

Латинский перевод книги Аль-Хорезми при описании правил всегда содержал такие слова: «Алгоризми говорил». По прошествии времени, люди стали забывать, что «Алгоризми» это не совсем чёткий перевод имени автора правил, и начали эти сформулированные правила считать алгоритмами. Таким образом фраза «Алгоризми говорил» превратилась в «алгоритм гласит». То есть термин «алгоритм» фактически произошёл от имени великого Аль-Хорезми. В качестве научного термина изначально он подразумевал только правила осуществления операций в десятичной системе счисления. Со временем, этот термин стал применяться в более широком смысле и под алгоритмом сегодня понимаются различные правила выполнения каких-либо процедур. Это основополагающий термин в дисциплинах, связанных с информатикой. В таблице ниже представлено написание цифр в разных вариантах:

Рисунок 1. Таблица символов. Автор24 — интернет-биржа студенческих работ

Применение арабской нумерации в Европе связывается с тем обстоятельством, что в границах сегодняшней Испании располагались две страны. Это христианское Барселонское графство и Кордовский Халифат, где правила мусульманская вера. Сильвестр второй был папой римским Христианской Церкви с девятьсот девяносто девятого года по тысяча третий и считался очень образованным и неплохим учёным. Он смог показать европейцам каких высот достигли арабы в математике и астрономии. Когда он был просто монахом, то имел возможность изучать арабские научные трактаты и книги. Но прошло ещё триста лет, прежде чем арабские цифры стали общепризнанными и прочно вошли в нашу жизнь.

Как набрать римские цифры на клавиатуре проще всего?

Нередко у начинающих пользователей персональных компьютеров возникает вопрос о том, как набрать римские цифры на клавиатуре.

Данная система счисления достаточно часто используется для маркировки списков, например. В рамках предлагаемого вашему вниманию материала будут описаны различные способы решения данной задачи.

На основании их сравнения будет выбран тот, которым проще всего пользоваться на практике.

Стандартное решение

Наиболее простой ответ на вопрос о том, как набрать римские цифры на клавиатуре – это использование английской раскладки клавиатуры. Она по умолчанию включена в каждой версии операционной системы «Виндовс», так что с процессом ввода проблем не должно возникнуть. Единственное, что нужно знать в таком случае – это набор цифр, которые в данной системе счисления используются. Сюда входят:

• «1» – это цифра «I» (альтернатива – английская буква «И»).
• «5» – это число «V» (в том же самом алфавите это «В»).
• «10» – это «Х» (можно поставить русскую «Х» или английскую «Икс»).
• «50» – обозначается как «L» (в латинской раскладке каждой клавиатуры она присутствует).
• «100» – это «С» (в этом случае все аналогично «10»).
• «500» – обозначается как «D».
• «1000» – в латинском счислении «М».

Комбинируя эти цифры, можно получить любое число. При этом стоит отметить один важный нюанс. Если перед большим числом находится меньшее, то оно вычитается из него. Например, IV – будет 4 в арабском исчислении.

А вот если все наоборот, после большего находится меньшее, то все суммируется. Как пример, можно привести 6 – VI. Зная эти правила, понять, как набрать римские цифры на клавиатуре, не составляет особого труда. Только вот не всегда все это можно помнить.

В таких случаях лучше всего сделать шпаргалку и при наборе таких чисел пользоваться ею.

ASCII-коды

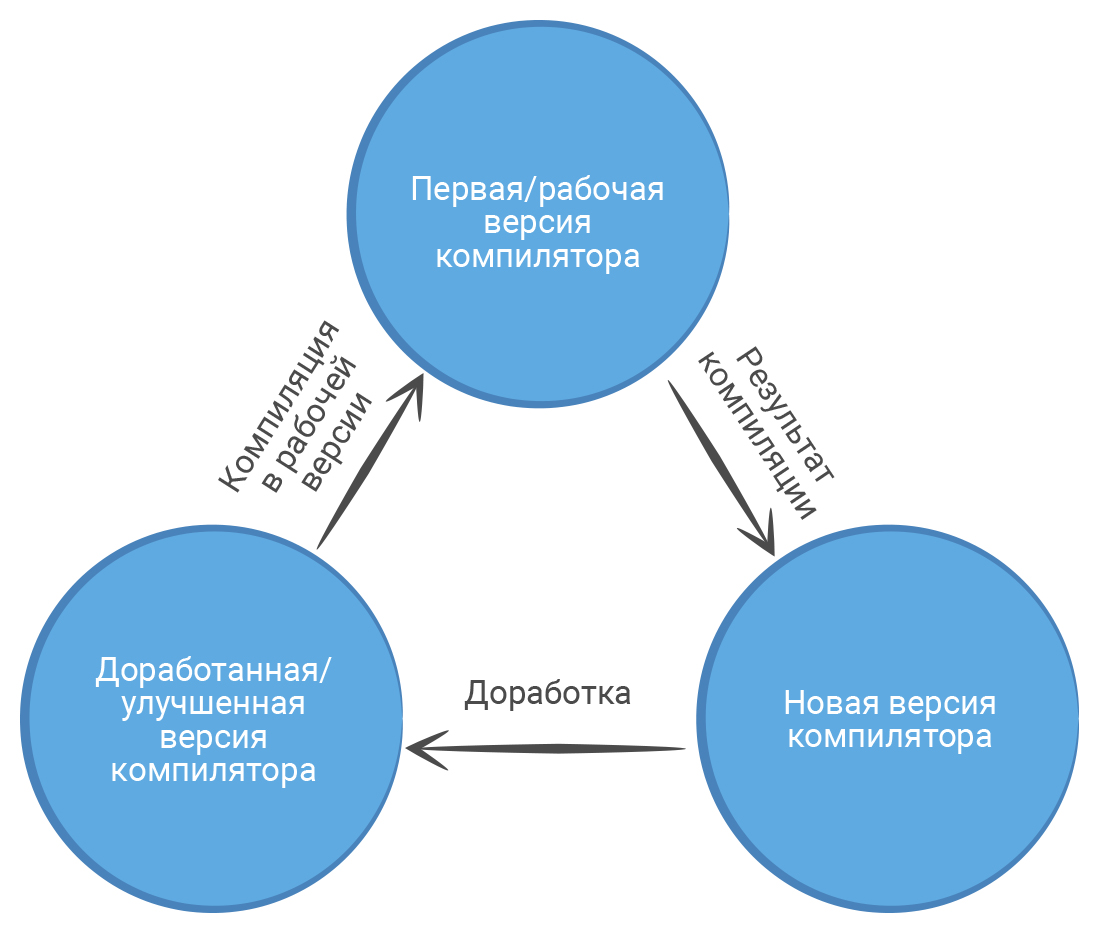
Альтернативным способом ввести римские цифры на клавиатуре ноутбука или стационарного компьютера является использование так называемых ASCII-кодов.

То есть те же самые английские буквы можно набрать комбинацией клавиш ALT и последовательным набором комбинации арабских чисел на расширенной клавиатуре (не забываем о том, что ключ Num Lock должен быть во включенном состоянии). Возможные комбинации кодов указаны в таблице 1.

Использование данного способа значительно все усложняет, поэтому проще применять на практике тот, который был приведен ранее.

Таблица 1.

ASCII – коды набора римских чисел.

№ п/п	Арабская цифра	Римская цифра	ASCII – код
1	1	I	73
2	5	V	86
3	10	Х	88
4	50	L	76
5	100	С	67
6	500	D	68
7	1000	М	77

“Ворд”

Наиболее просто латинские цифры на клавиатуре набрать в “Ворде” или любом другом офисном приложении. Для этого в данной группе приложений предусмотрена специальная функция. Порядок набора в данном случае следующий:

• Нажимаем комбинацию клавиш Ctrl и F9.
• Далее запустится специальная функция пересчета и появятся скобки {}. В них нужно набрать следующее =нужное_арабское_число\*ROMAN.
• Затем нажимаем функциональную клавишу F9.
• После этого наше арабское число преобразуется в римское.

Приведенный алгоритм действительно проще ранее описанных. Но у него есть один существенный недостаток – работает он только в офисных приложениях, и если нужно в фотошопе набрать какое-то римское число, то им уже невозможно воспользоваться. В крайнем случае можно нужное число набрать здесь. Затем выделить с помощью манипулятора, скопировать и затем вставить в другое приложение.

Резюме

В рамках данного материала были предложены различные способы того, как набрать римские цифры на клавиатуре. Сравнив их, можно прийти к выводу, что проще всего использовать английский алфавит, в котором есть все необходимые числа.

Такое решение работает во всех без исключения приложениях. Единственный его недостаток – это необходимость знать цифры данной системы счисления. Но этот вопрос можно решить. Если часто приходится пользоваться римскими числами, то вы и так запомните их.

Ну а в крайнем случае можно сделать черновик, который значительно упростит данную задачу.

Как появился ноль

Некоторым может показаться очевидным, что ноль является частью позиционной системы, но это неверно, поскольку в человеческой истории он появился относительно недавно. Но на самом деле этот вездесущий символ, который обозначает «ничто», не использовался в Европе вплоть до XII века. Считается, что первые попытки введения в позиционную систему ноля были предприняты в древней Месопотамии. Шумерские писцы использовали различные значки и символы, которые по своим функциям приближались к этой цифре, еще четыре тысячи лет назад. Хотя первые письменные документы о появлении подобного знака датируются III-II тысячелетием до н. э. в Вавилоне. В специфической шестидесятиричной вавилонской цифровой системе существовал знак, который помогал отличить десятки, сотни и тысячи, хотя отдельно он не употреблялся. Т. е. эта цифра еще не обрела все свои современные функции.

Индо-арабская цифровая система появилась в Индии приблизительно в 500 году нашей эры. Она была более революционной, поскольку в ней был ноль и позиционная система счисления. Это стало значительным прогрессом с точки зрения математики. Так ответ на вопрос «сколько арабских цифр существует», изменился, поскольку ноль стал еще одной полноценной цифрой.

Иногда в позиционной системе счисления различают цифры и глифы, символы, которые используются для графического изображения цифр или букв. Первая запись ноля в форме глифа датируется IX веком (в центральной Индии). Многочисленные сохранившиеся индийские медные таблички подтверждают существование символа, аналогичного по своим функциям нулю, уже в VI в. н. э.

Сравнение семитских букв и современных цифр

1
соответствует первой букве алфавитов:

• финикийского —
• древнееврейского — א
  или прописной —
• арабского- или

Что мы видим? Вертикальная часть финикийской буквы в древнееврейском алфавите наклонилась влево (в прописи в древнееврейском вправо). Горизонтальная обвеска видоизменилась: превратилась в опору слева и приподнялась справа, а в прописи превратилась в скобку справа от вертикальной черты. В арабском алфавите наклон влево стал меньше, почти невидим, а обвеска ушла в хамзу , которая ставится сверху или (реже) снизу алифа. Во всех трёх случаях ясно прослеживается единица: вертикальная черта и, как правило, клювик (обвеска) слева. Современный клювик может быть в написании длиннее (англо-американское написание) или короче (например, русское написание) или вообще отсутствовать. Вывод: цифра 1 — видоизмененная семитская (финикийская, древнееврейская, арабская) буква алеф. 2
соответствует второй букве (ба) алфавитов:

финикийского —

• древнееврейского — ב
  или прописной —
• арабского —

Что мы видим? Образование в финикийском, эволюцию в древнееврейском и закат (опрокидывание) в арабском алфавитах верхней части буквы, похожей на верхнюю часть цифры 2. Основание букв зеркально перевернулось, что бывает при переходе от письма справа-налево к письму слева-направо. Вывод: цифра 2 — видоизмененная семитская (прежде всего, финикийская и древнееврейская) буква бет. 3
соответствует третьей букве (джим) алфавитов:

финикийского —

арабского —

Что мы видим? В финикийской букве начинает формироваться верхняя часть тройки, в древнееврейской формируется средняя часть, а в арабской, с учетом зеркальности — нижняя часть. Вывод: цифра 3 — видоизмененная семитская (финикийская, древнееврейская и арабская) буква гимель (джим). 4
соответствует четвертой букве (даль) алфавитов:

финикийского —

• древнееврейского — или прописной —
• арабского —

Что мы видим? Нижний сторона треугольника финикийской буквы приподнимается в древнееврейской букве и почти сливается с верхней, создавая утолщение или выступ. Вертикальная сторона остается на месте. Особенно похожа на четверку прописная древнееврейская буква, если посмотреть на ее зеркальное отражение. Промежуточная стадия, которая, возможно, была в какой-то период — вылитая четверка. Арабская буква, сглаженное написание древнееврейской, вряд ли серьёзно повлияла на написание четверки. Вывод: цифра 4 — видоизмененная семитская (прежде всего финикийская и древнееврейская) буква далет. 5
соответствует пятой букве (ха) алфавитов:

финикийского —

• древнееврейского — ה
  или прописной —
• арабского —

Что мы видим? Если перевернуть финикийскую и древнееврейскую буквы зеркально, сверху образуется козырек пятерки, а средняя и нижняя часть переходят в закругление, которое закрепляется в арабской букве. Вывод: цифра 5 — видоизмененная семитская (финикийская, древнееврейская и арабская) буква хей. 6
соответствует шестой букве (уа) алфавитов:

финикийского —

• древнееврейского — ו
• арабского —

Что мы видим? В финикийском один из козырьков уходит, а вертикальная черта выгибается, в древнееврейском вертикальная черта выгибается, буква зеркально переворачивается. В арабском аналогично. Вывод: цифра 6 — видоизмененная семитская (финикийская, древнееврейская и арабская) буква вав. 7
соответствует седьмой букве (зай) алфавитов:

финикийского —

• древнееврейского —
• арабского —

Что мы видим? Основание финикийской буквы пропадает, козырек сдвигается влево. В результате, чем не семёрка? Вывод: цифра 7 — видоизмененная семитская (финикийская, древнееврейская и арабская) буква зайн (зай). 8
соответствует восьмой букве (ха) алфавитов:

финикийского —

арабского —

Что мы видим? Финикийская буква очень похожа, древнееврейская потеряла основание, а арабская — макушку. Вывод: цифра 8 — видоизмененная семитская (финикийская, древнееврейская и арабская) буква хет (ха). 9
соответствует восьмой букве (та) алфавитов:

финикийского —

• древнееврейского — и прописной —
• арабского — или

Что мы видим? Финикийская буква включает в своем образе девятку. Далее все упрощается в древнееврейской букве, в которой, если её повернуть слегка против часовой стрелки, видна девятка. В арабской букве при аналогичном условии девятка тоже видна. Вывод: цифра 9 — видоизмененная семитская (финикийская, древнееврейская и арабская) буква тет (та).

Часть 3. Реконструкция событий.

Давным-давно наши предки решили основательно упорядочить свою жизнь. С этой целью они придумали календарь. По причине того, что периоды Луны были более короткими, а значит, легче заметными, чем солнечные. Поэтому, первым был создан лунный календарь, в котором 27 дней каждого месяца были разделёны на три периода (три недели) по 9 дней. В русских сказках эта информация сохранилась в виде слов: «у отца было три сына» (у месяца три периода), «тридевятое царство», «за тридевять земель». Да и умерших поминали на девятый день. Это очень удобно – не надо считать дни. Если в пятницу умер, то ровно через неделю, в следующую пятницу, поминают.

Действительно, славянская неделя состояла из девяти дней:

1.	ПонедЕльник.
2.	ВтОрник.
3.	ТретЕйник.
4.	ЧетвЕрик.
5.	ПятнИца.
6.	ШестИца.
7.	СедьмИца.
8.	ОсьмИца.
9.	НедЕля.

Последний – девятый – день был выходным, когда ничего не делали. Потому он и назван «неделя». Здесь всё понятно. Но почему первый день недели назван не первиком или, к примеру, первейником? Ответ напрашивается сам собой: потому, что один или единица – это фаллический символ бога, его имя. А имя бога нельзя произносить в быту (в суе). Оно было тайным. Пришлось скрыть истинное название, и первый день назвали понедельником – тот, который после недели, после выходного дня.

Как мы видим, числа в те времена уже были или только начинали создаваться, но цифр ещё не было. Предполагается также, что письменность уже существовала. Естественно, что со временем встал вопрос обозначения чисел при письме.

Как бы то ни было, но именно эти девять дней, точнее – девять цифр, им соответствующих – легли в основу первой, древней системы счисления. Со временем, после изобретения ноля, эта система стала десятичной. И десять пальцев на руках не имеют к этой системе никакого отношения. Это просто совпадение.

Telecar.

24 июня 2014 г.

Откуда взялись современные числовые знаки от 1 до 10

Зарождение арабских цифр относят к древней южной Индии. Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.

В цифрах встречаются признаки букв арамейского, греческого и финикийского алфавитов. Предположительно числовые знаки начали зарождаться во 2 веке до нашей эры, в то время, когда существовало Индо-греческое царство.

В отличие от счета в русском языке — один (1), два (2), три (3), арабские цифры имеют свое название:

• 1 (один) — 1 Уахид;
• 2 (два) — 2 Итнан;
• 3 (три) — 3 Талата;
• 4 (четыре) — 4 Арба-а;
• 5 (пять) — 5 Хамиза;
• 6 (шесть) — 6 Ситта;
• 7 (семь) — 7 Саба-а;
• 8 (восемь) — 8 Таманиа;
• 9 (девять) — 9 Тизза;
• 10 (десять) — 10 Ашара.