Как строить графики в excel?

OnlineCharts.ru

Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.

Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.

Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.

Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.

После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.

Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.

Также можно определить цвет.

Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.

Нажимаем далее и попадаем во вкладку «Просмотр», где получаем возможность созерцать плоды своего труда.

На вкладке «Сохранить и поделиться диаграммой» есть возможность отправить ссылку на созданный график друзьям или поделиться своей работой через социальные сети.

Все предельно просто.

Kontrolnaya-Rabota.ru

• Построение двухмерного графика функции в декартовых и полярных координатах.
• Построение графика, заданного параметрически.
• Построение 3D графиков (поверхностей), заданных уравнением.
• Построение гистограмм и графиков и по точкам.
• Построение графиков неявно заданных функций.

Пользователю достаточно ввести в онлайн-программу данные из условия задачи и кликнуть кнопку «Построить график».

Запутаться сложно, так как каждая страница этого раздела сопровождается пояснениями и примерами. Там же даны подсказки, какие символы и сокращения следует использовать при вводе выражений.

При построении 2D-графика в декартовых координатах приводится подробный результат исследования функции, чего не встретишь практически нигде.

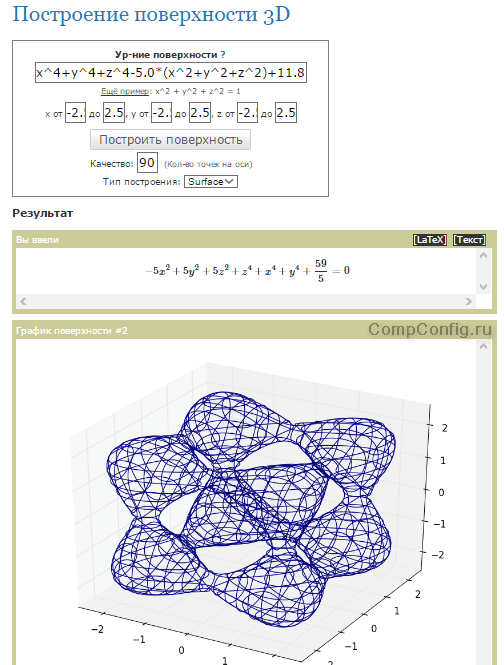
Достоинства сервиса kontrolnaya-rabota.ru — возможность пользоваться им без ограничений, выдача результатов с ходом решения, быстрые и точные ответы, наличие других онлайн-калькуляторов для вычисления уравнений, интегралов, неравенств и прочего. А недостаток — в том, что не все чертежи можно масштабировать. Это создает определенные неудобства при копировании.

Excel: методика создания графика функции

Это уже более нетривиальная задача, и для ее выполнения необходимо выполнить два основных действия:

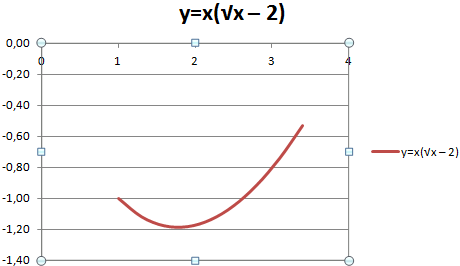
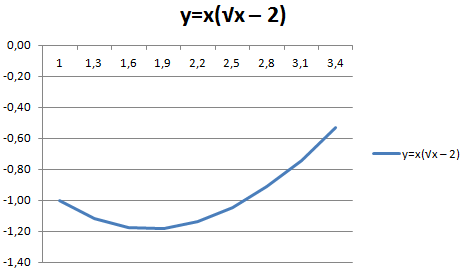
1. Сформировать таблицу, служащую источником информации. Сперва следует определиться с тем, какая будет конкретно в вашем случае использоваться функция. Например, y=x(√x – 2). При этом в качестве используемого шага мы выберем значение 0,3.
2. Собственно, построить график.

Итак, нам необходимо сформировать таблицу, где есть два столбца. Первый – это горизонтальная ось (то есть, X), второй – вертикальная (Y). Вторая строка содержит первое значение, в нашем случае это единица. На третьей строке нужно написать значение, которое будет на 0,3 большим предыдущего. Это можно сделать как с помощью самостоятельных подсчетов, так и записав непосредственно формулу, которая в нашем случае будет следующей:

=A2+0,3.

После этого нужно применить автозаполнение к следующим ячейкам. Для этого нужно выделить ячейки A2 и A3 и перетащить квадратик на нужное количество строк вниз.

16

В вертикальной колонке мы указываем формулу, используемую, чтобы на основе готовой формулы построить график функции. В случае с нашим примером это будет =А2*(КОРЕНЬ(А2-2). После этого подтверждает свои действия с помощью клавиши Enter, и программа автоматически рассчитает результат.

17

Далее нужно создать новый лист или перейти на другой, но уже существующий. Правда, если есть острая необходимость, можно вставить диаграмму здесь же (не резервируя под эту задачу отдельный лист). Но лишь при условии, что есть много свободного пространства. Затем нажимаем следующие пункты: «Вставка» – «Диаграмма» – «Точечная».

После этого надо решить, какой тип диаграммы нужно использовать. Далее делается правый клик мышью по той части диаграммы, для которой будут определяться данные. То есть, после открытия контекстного меню следует нажать на кнопку «Выбрать данные».

Далее нужно выделить первый столбик, и нажать «Добавить». Появится диалоговое окно, где будут настройки названия ряда, а также значения горизонтальной и вертикальной осей.

18

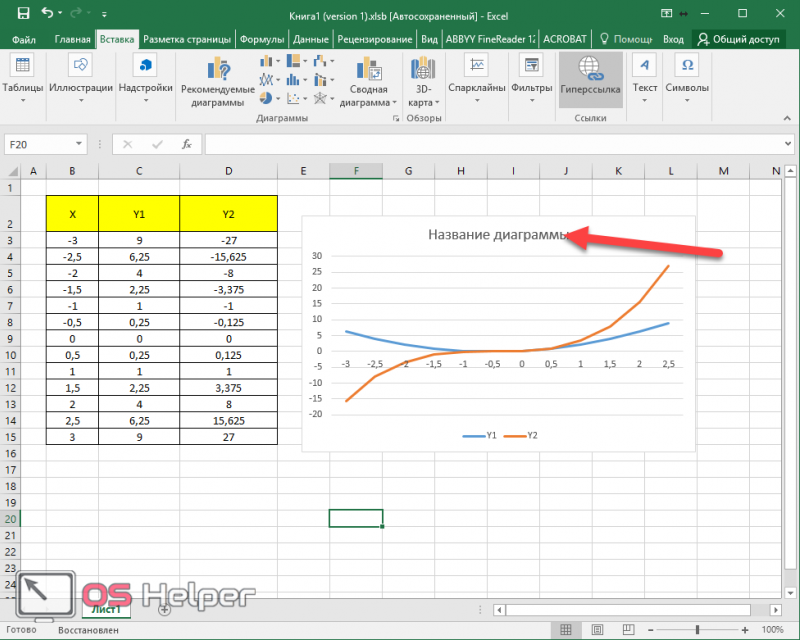
Ура, результат есть, и выглядит очень даже мило.

19

Аналогично графику, построенному в начале, можно удалять легенду, поскольку мы имеем только одну линию, и нет необходимости ее дополнительно подписывать.

Но есть одна проблема – на оси X не нанесены значения, лишь номер точек. Чтобы скорректировать эту проблему, надо дать названия этой оси. Чтобы это сделать, нужно кликнуть правой кнопкой мыши по ней, а затем выбрать пункт «Выбрать данные» – «Изменить подписи горизонтальной оси». По окончании этих операций выделяется требуемый набор значений, и график станет выглядет так.

20

SMath Studio

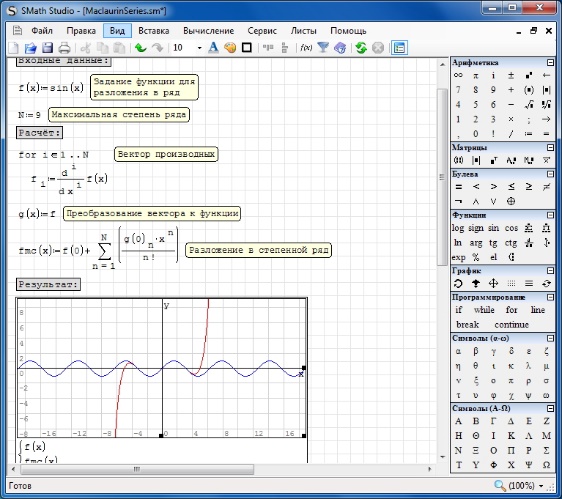
SMath Studio

Вообще, эта утилита предназначена для математических вычислений. Но также она умеет строить двумерные графики любой сложности и работает почти со всеми функциями. Однако базовый функционал у программы довольно скудный.

Тем не менее, утилита обладает понятным интерфейсом. Хоть и без русского языка. Ею очень легко пользоваться. И именно поэтому новички предпочитают этот продукт. Тем более, что он совершенно бесплатен и скачать его можно с официального сайта разработчика.

ПЛЮСЫ:

• Построение двумерных графиков любой сложности
• Работа со всеми математическими функциями
• Простой и понятный интерфейс
• Занимает мало места

МИНУСЫ:

Нет русского языка

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина: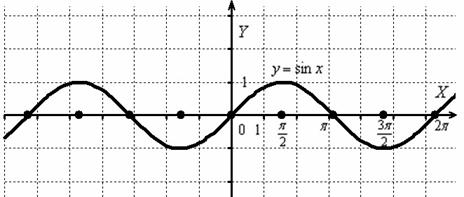
Согласно правилу, при  график сохраняется: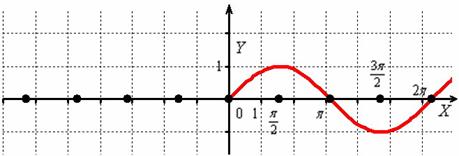
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость: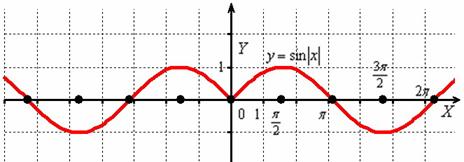

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае: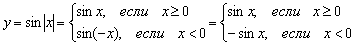

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: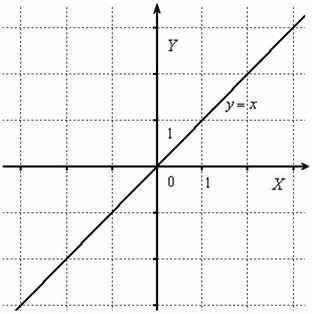
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость: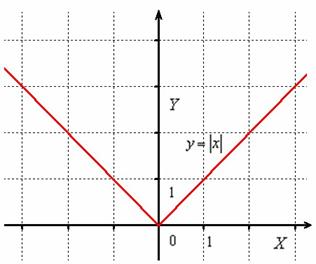

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)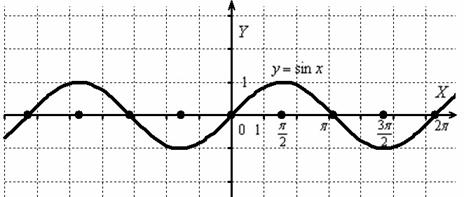

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :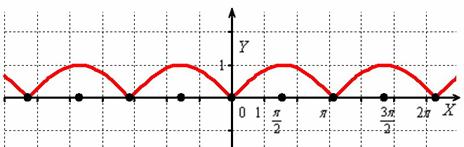

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем: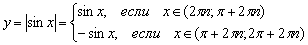, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)

ChartGo

Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.

Для обучения пользователям представляется подробное руководство и деморолики.

ChartGo будет полезен для тех, кто нуждается в создании диаграмм регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».

Построение графиков онлайн осуществляется по таблице.

В начале работы необходимо выбрать одну из разновидностей диаграмм.

Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.

Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.

Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.

Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.

Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.

Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий

Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.

Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.

Программа имеет гибко настраиваемый интерфейс.

После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.

OpenOffice Calc

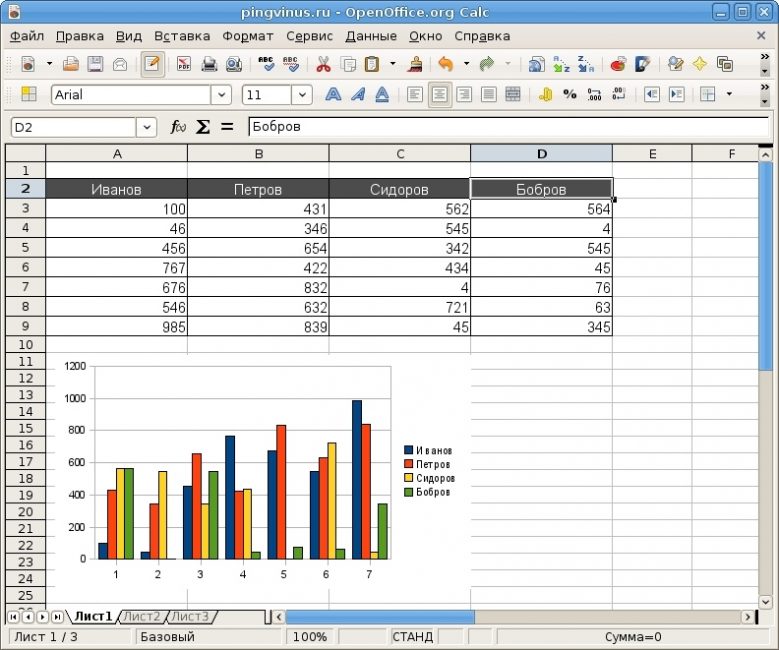
OpenOffice Calc

Это приложение является частью свободного офисного пакета OpenOffice. Оно позволяет быстро создать двумерный график по заданной функции. Однако дополнительных возможностей, к сожалению, нет. Да и первоочередная задача у продукта совсем другая – вычисления.

Тем не менее, программа позволяет создавать графики. Поэтому она и попала в данный список. К числу преимуществ приложения стоит отнести очень простой интерфейс и наличие русского языка. Поэтому если нужен простой график, то пользователи запускают OpenOffice Calc.

ПЛЮСЫ:

• Очень простой интерфейс
• Построение двумерных графиков по заданным функциям
• Сохранение результата
• Есть русский язык

МИНУСЫ:

Скудный функционал

MathGrapher

MathGrapher

Превосходная программа для построения графиков, обладающая весьма понятным интерфейсом. Этот продукт (один из немногих) может сохранять графики в форматах fct, grd, bmp, jpg, eps, png, или mwf. Такое богатое количество форматов – только плюс.

В то же время утилита способна работать с производными и первообразными функциями. Оформление у программы приятное. Однако русского языка в интерфейсе очень не хватает. Продукт является полностью бесплатным. Его можно скачать на сайте разработчика.

ПЛЮСЫ:

• Конвертирование графика в огромное количество форматов
• Быстрое построение 2D графиков
• Простой и понятный интерфейс
• Работа с производными и первообразными функциями

МИНУСЫ:

Нет русского языка

Построение графиков других функций

Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.

Квадратичная функция  y=ax2+bx+c

Выполните следующие действия:

• В первой строке меняем заголовок
• В третьей строке указываем коэффициенты и их значения
• В ячейку A6 записываем обозначение функции
• В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
• Копируем её на весь диапазон значений аргумента вправо

Получаем результат

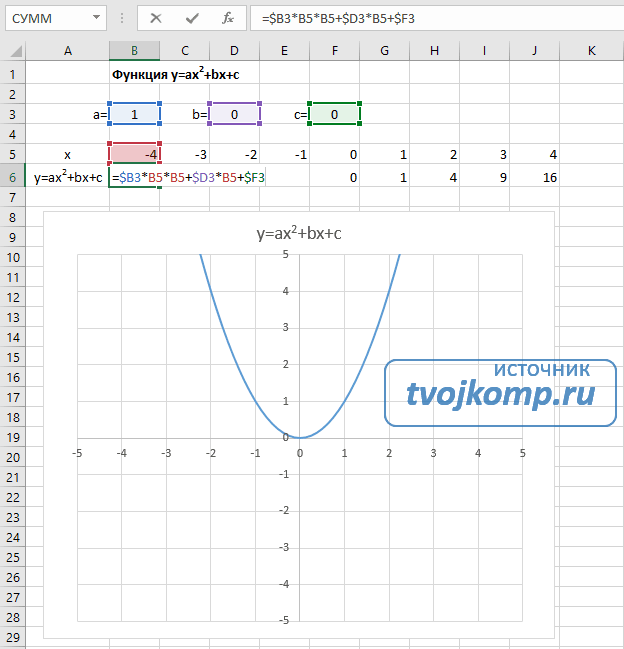
График квадратичной функции

Кубическая парабола  y=ax3

Для построения выполните следующие действия:

• В первой строке меняем заголовок
• В третьей строке указываем коэффициенты и их значения
• В ячейку A6 записываем обозначение функции
• В ячейку B6 вписываем формулу =$B3*B5*B5*B5
• Копируем её на весь диапазон значений аргумента вправо

Получаем результат

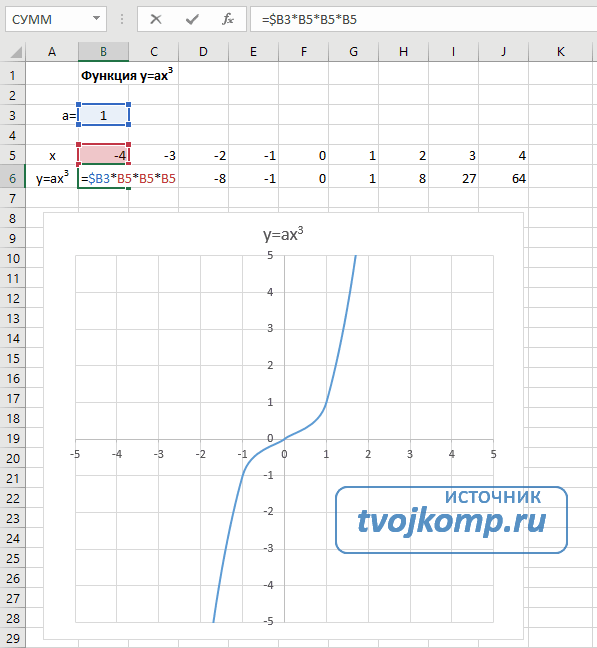
График кубической параболы

Гипербола  y=k/x

Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.

Далее выполните действия:

• В первой строке меняем заголовок.
• В третьей строке указываем коэффициенты и их значения.
• В ячейку A6 записываем обозначение функции.
• В ячейку B6 вписываем формулу =$B3/B5
• Копируем её на весь диапазон значений аргумента вправо.
• Удаляем формулу из ячейки I6.

Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.

• Кликните диаграмму
• На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
• Откроется окно мастера ввода данных
• Выделите мышкой прямоугольный диапазон ячеек A5:P6
• Нажмите ОК в окне мастера.

Получаем результат

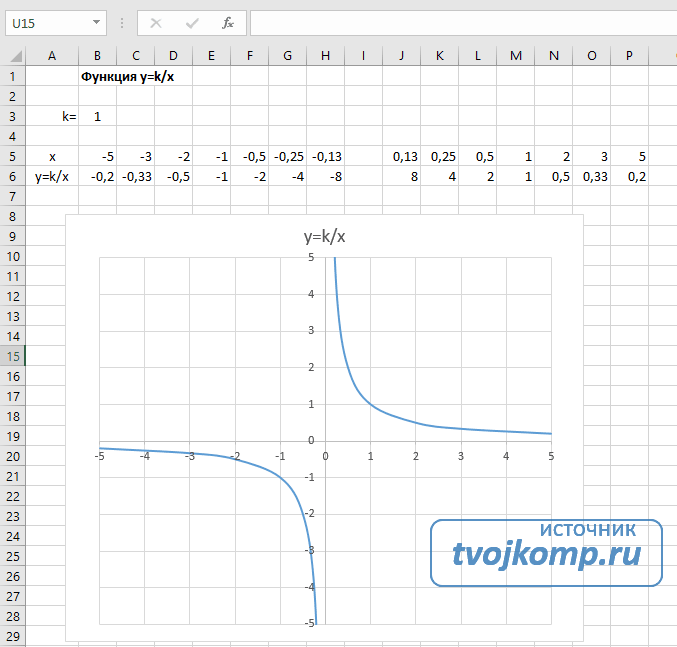
График гиперболы

Построение тригонометрических функций sin(x) и cos(x)

Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x). Сначала заполните таблицу как на рисунке ниже

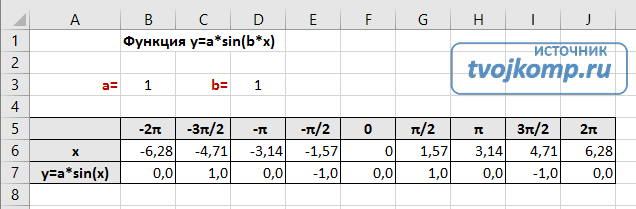
Таблица значений функции sin(x)

В первой строке записано название тригонометрической функции. В третьей строке прописаны коэффициенты и их значения

Обратите внимание на ячейки, в которые вписаны значения коэффициентов. В пятой строке таблицы прописываются значения углов в радианах

Эти значения будут использоваться для подписей на графике. В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; … В седьмой строке записываются расчетные формулы тригонометрической функции.

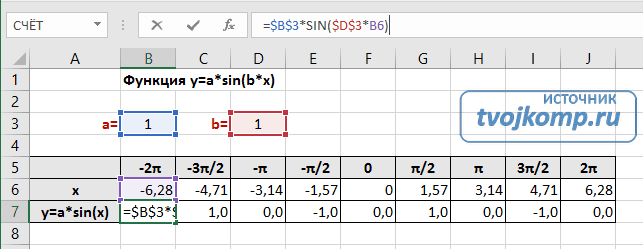
Запись расчетной формулы функции sin(x) в Excel

В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице. После заполнения таблицы приступаем к построению графика.

Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами. 

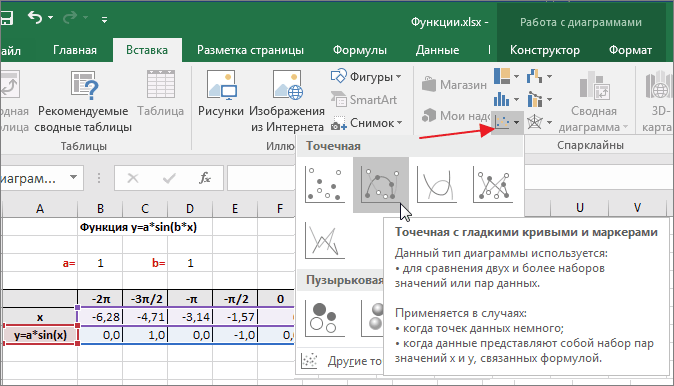
Построение диаграммы Точечная с гладкими кривыми

В итоге получим диаграмму.

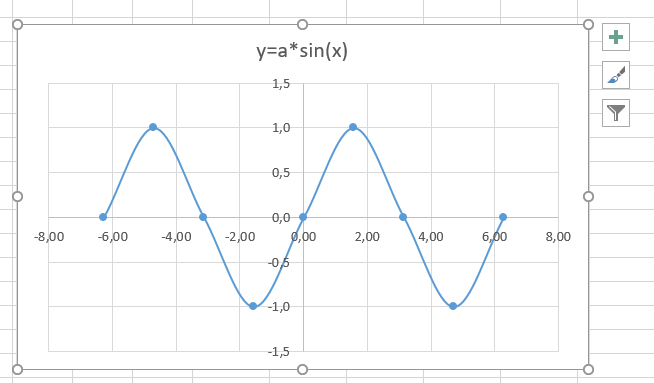
График sin(x) после вставки диаграммы

Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.

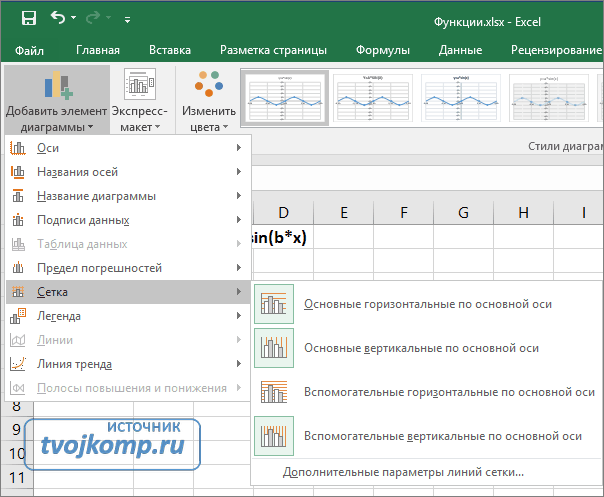
Настройка сетки при построении графика

Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.

Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.

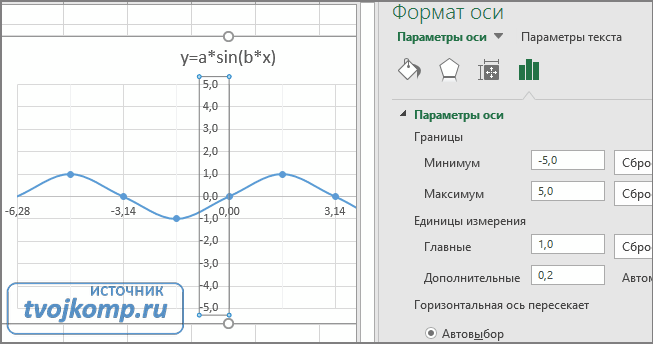
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.

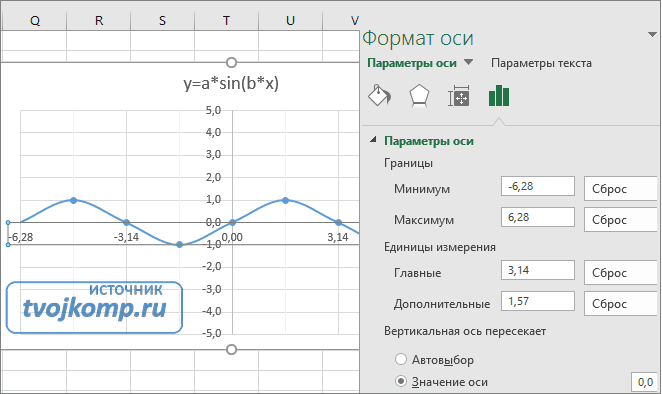
Настройка формата горизонтальной оси Х графика функции

Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5. Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.

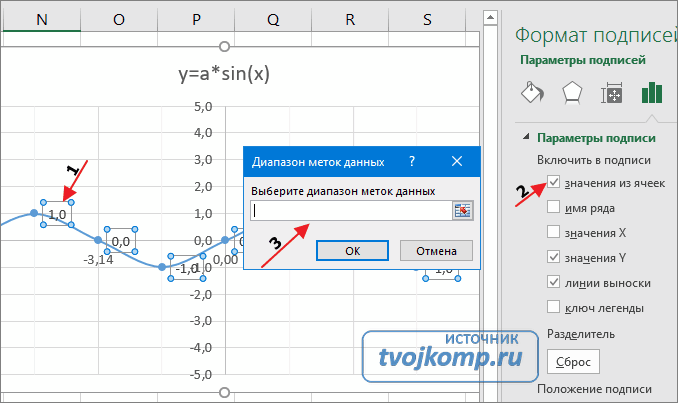
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.

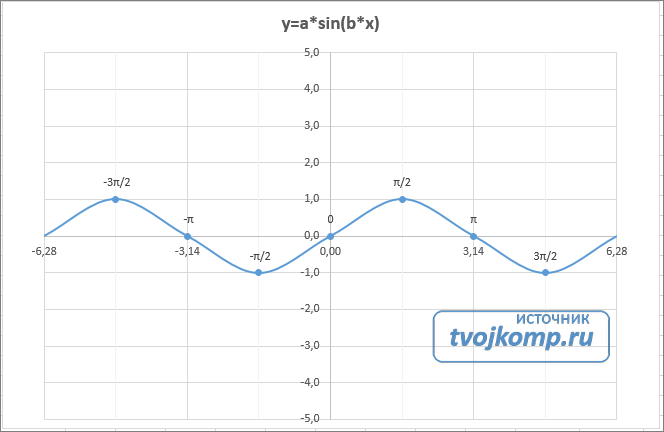
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.

PS: Интересные факты про логотипы известных компаний

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Проще всего освоить такой материал на веселых задачках — в детской школе Skysmrt подобрали тысячи интерактивных упражнений разной сложности, чтобы ребенок нагнал упущенное и повысил оценки в школе без давления и суеты.

Приходите на бесплатный вводный урок математики: покажем, как все устроено и вдохновим на учебу.

Как построить график

1. Для создания графика в программе Эксель, в первую очередь, потребуется ее основа с информацией. Другими словами, сначала необходимо создать таблицу и внести в неё все значения, на базе которых будет строиться график. Или же можно открыть файл, который содержит таблицу.
2. Переходим во вкладку «Вставка». Выделяем всю таблицу или только ту часть, которую необходимо отразить в виде графика. Нажимаем на кнопку «График».
3. На выбор будет предоставлены различные варианты графиков.
   • График. Привычные нам простые линии.
   • График с накоплением. При выборе данного варианта будет отображаться динамика изменения вклада каждого значения с течением времени или по категориям данных, которые разделены на равные интервалы.
   • Нормированный график с накоплением. Если выбрать данный вариант, будет отображаться динамика вклада каждой величины в процентах с течением времени или по категориям данных, которые разделены на равные интервалы.
   • График с маркерами (обычный, с накоплением или нормированный с накоплением). Будут отображаться конкретные значения данных на графике.
   • Объёмный график. Имеет кроме высоты и длины, еще и глубину. Кривая графика изображается в виде ленты.
   • График с областями (обычный, с накоплением, нормированный с накоплением). Сами принцип построения линий в зависимости от выбранного подвида аналогичен описанным выше вариантам. Однако, в данном случае, график представляет из себя не просто линии, а закрашенные области согласно построенными линиям.
   • Объемный график с областями (обычный, с накоплением, нормированный с накоплением). Все то же самое, что и в варианте выше, только в трехмерном исполнении.
4. Выбираем из перечисленных вариантов наиболее понравившийся или тот, что лучше всего отобразит необходимую информацию, и щелкаем по нему.
5. Об остальном позаботится Эксель, выведя результат в виде готового графика в отдельном окне, которое, к тому же, можно изменять по размерам путем растягивания или сжатия, а также, перемещать внутри листа.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:
Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

Umath.ru

Веб-сервис Umath.ru — не только набор онлайн-калькуляторов, но и неплохой справочник по математике. Позволяет строить 3 разновидности графиков функций:

• Заданных уравнением.
• Заданных параметрически.
• В полярной системе координат.

В отличие от предыдущего, этот веб-сайт дает возможность размещать несколько графиков на одной плоскости (они будут нарисованы разным цветом). Также он позволяет изменять масштаб и смещать положение центра координатного пространства (кнопки управления находятся слева от графика, но можно пользоваться и мышью).

Готовый результат можно скачать на компьютер в виде картинки.

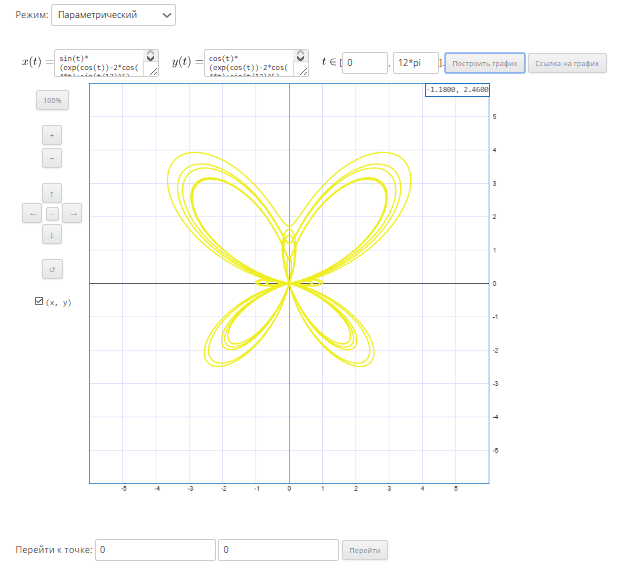
Достоинства Umath.ru — простота применения (на станице есть пояснения, списки функций и констант), масштабирование, возможность оставлять комментарии, пользоваться справочником и другими математическими калькуляторами. Недостаток — ограниченный функционал (к сожалению, нет возможности строить трехмерные графики) и иногда проскакивающие ошибки. Но, надеемся, это временно, так как сервис активно развивается.