Руководство по классу java integer

2 Алгебраические функции в Java

В большинстве случаев программисту с головой хватает школьной математики: даже синусы и косинусы в коде можно встретить очень редко. Чаще всего они нужны при работе с играми, картами или игровыми движками. 90% программистов с этим никогда не сталкиваются.

Но, кроме геометрии, программистам иногда приходится использовать и алгебраические функции. И, конечно же, класс содержит самые распространенные из них:

Метод	Описание
	квадратный корень из
	кубический корень из
	возведение в степень:
	экспонента:
	натуральный логарифм :
	десятичный логарифм :
	натуральный логарифм :

Если вам нужен квадратный или кубический корень из числа, для этого есть функции и .

Корень из двух можно вычислить так:

Если вы хотите получить корень более высокой степени, воспользуйтесь функцией возведения в степень: в степени — это и будет корень четвертой степени, и т.д.

Для работы с логарифмами и экспонентами есть функции – натуральный логарифм и — экспонента. Для вычисления десятичного логарифма есть функция .

Если вам нужен логарифм числа по основанию , воспользуйтесь простой формулой:

Полезные функции

Последние две функции и могут быть вам полезны, если вы проводите вычисления при очень маленьких значениях .

При сложении очень маленьких и очень больших переменных часто может возникнуть ситуация, когда очень маленькое значение просто игнорируется (отбрасывается) как незначащее. Это, собственно, и будет происходить, если использовать функции и . Поэтому программисты придумали функции, которые возвращают только ту самую «маленькую значащую часть»

Пример:

Вы хотите посчитать натуральный логарифм от , где равен . Вы просто не сможете передать это число в функцию , т.к. если сложить и , получится . — настолько маленькое число, что будет отброшено полностью при сложении чисел.

А т.к. в математике часто приходится вычислять при числах, близких к , программисты придумали способ обойти эту проблему: передать в функцию не само число, а только его отличие от .

4 Деление целых и вещественных чисел в Java

При делении целого числа на целое остаток всегда отбрасывается. Как же тогда, скажем, поделить на , чтобы получить ?

Поначалу кажется, что правильный вариант такой:

Однако не все так просто. Дело в том, что Java-машина сначала вычислит значение выражения и только потом присвоит результат в переменную . А деление выполнится нацело. Т.е.  будет содержать или, если быть более точным,

Правильный вариант такой: хотя бы одно из чисел, участвующих в делении, нужно записать как вещественное (т.е. с точкой):

В любом из этих выражений  будет содержать значение

А как же быть с переменными? Что если у нас есть такой код:

Тут есть хитрое (и очевидное) решение — заставить Java-машину преобразовать переменные в вещественные, умножив их на вещественную единицу — 

Обратите внимание, что у операций умножения и деления равный приоритет, и они выполняются слева направо, поэтому имеет значение, где именно мы умножаем на вещественную единицу. Примеры:

Примеры:

Команда	Порядок выполнения	Результат

Добивайтесь большего меньшими усилиями

Как говорится, наиболее эффективным является код, который попросту не пришлось писать. Поэтому не стоит делать то, что уже сделано экспертами до вас. Код, использующий как новые, так и старые методы класса , будет быстрее, эффективнее и точнее, чем тот, что вы напишете сами. Просто используйте его.

Похожие темы

Оригинал статьи: Java’s new math, Part 1: Real numbers (Эллиотт Расти Гарольд, developerWorks, октябрь 2008). (EN)
Не пропустите вторую статью в этой серии под названием Новые математические возможности Java, часть 2: числа с плавающей точкой (Эллиотт Расти Гарольд, developerWorks, январь 2009), в которой рассматриваются функции, созданные для выполнения операций над числами с плавающей точкой.
Прочитайте главу 4 спецификации языка Java под названием , в которой описываются арифметические операции над числами с плавающей точкой. (EN)
Ознакомьтесь со стандартом IEEE 754: Стандарт IEEE на двоичную арифметику с плавающей точкой, в котором определена арифметика с плавающей точкой, использующаяся в большинстве современных процессорах и языках, в том числе в Java. (EN)
Прочитайте документацию по классу , в которой описаны функции, обсуждаемые в этой статье

(EN)
Обратите внимание на Сообщение об ошибке 5005861, в которой разочарованный пользователь требует более быстрой реализации тригонометрических функций в JDK. (EN)
В статье Цепная линия в Википедии рассказывается об истории и математическом смысле цепной линии

(EN)

: данную библиотеку, написанную на языке С и реализующую арифметику с плавающей точкой в соответствии со стандартом IEEE 745, можно загрузить из репозитория математического программного обеспечения Netlib. (EN)

OpenJDK: взгляните на исходный код математических классов в этой открытой реализации Java SE. (EN)
Сотни статей по всем аспектам программирования на Java можно найти на сайте developerWorks, в разделе Технология Java.

Символьные типыCharacter types

Тип является типом символьного представления, который эффективно кодирует члены базовой кодировки выполнения.The type is a character representation type that efficiently encodes members of the basic execution character set. Компилятор C++ обрабатывает переменные типа , и, в отличие от разных типов.The C++ compiler treats variables of type , , and as having different types.

Зависящие от Майкрософт: переменные типа помещаются в тип по умолчанию, если не используется параметр компиляции.Microsoft-specific: Variables of type are promoted to as if from type by default, unless the compilation option is used. В этом случае они рассматриваются как тип и переносятся в без расширения знака.In this case, they’re treated as type and are promoted to without sign extension.

Переменная типа является расширенным символом или типом многобайтового символа.A variable of type is a wide-character or multibyte character type. Используйте префикс перед символьным или строковым литералом, чтобы указать тип расширенных символов.Use the prefix before a character or string literal to specify the wide-character type.

Для конкретного Майкрософт: по умолчанию является собственным типом, но можно использовать для создания определения типа для .Microsoft-specific: By default, is a native type, but you can use to make a typedef for . Тип является синонимом для собственного типа, характерным для Microsoft .The type is a Microsoft-specific synonym for the native type.

Тип используется для символьного представления UTF-8.The type is used for UTF-8 character representation. Он имеет то же представление , что и, но обрабатывается компилятором как отдельный тип.It has the same representation as , but is treated as a distinct type by the compiler. Тип является новым в c++ 20.The type is new in C++20. Для Майкрософт: для использования требуется параметр компилятора.Microsoft-specific: use of requires the compiler option.

Тип используется для символьного представления UTF-16.The type is used for UTF-16 character representation. Он должен быть достаточно большим, чтобы представлять любой блок кода UTF-16.It must be large enough to represent any UTF-16 code unit. Компилятор обрабатывает его как отдельный тип.It’s treated as a distinct type by the compiler.

Тип используется для символьного представления UTF-32.The type is used for UTF-32 character representation. Он должен быть достаточно большим, чтобы представлять любую единицу кода UTF-32.It must be large enough to represent any UTF-32 code unit. Компилятор обрабатывает его как отдельный тип.It’s treated as a distinct type by the compiler.

Тернарная операция

Операция «?:» называется тернарной, потому что он принимает три операнда.

<выражение_boolean> ? <выражение1> : <выражение2>

1	<выражение_boolean> ? <выражение1> : <выражение2>

Тернарная операция вычисляет
<выражение_boolean>, если оно равно
true, то вычисляет и возвращает
<выражение1>, а если
false, то
<выражение2> .

Java

class Main {
public static void main(String[] args) {
int x = 3 > 2 ? 5 : -3; // 5
String str1 = 3 == 2 ? «YES»: «NO»; //»NO»
System.out.println(x);
System.out.println(str1);
}
}

1 2 3 4 5 6 7 8

classMain{ publicstaticvoidmain(Stringargs){ intx=3>2?5-3;// 5 Stringstr1=3==2?»YES»»NO»;//»NO» System.out.println(x); System.out.println(str1); } }

3 Класс Character

Класс в первую очередь интересен большим количеством утилитных статических методов, которые позволяют проверять символы на принадлежность разным категориям.

Примеры

Методы	Описание
	Проверяет, является ли символ символом алфавита
	Является ли символ буквой
	Является ли символ цифрой
	Является ли символ пробелом, символом переноса строки или смены параграфа (коды: 12, 13, 14)
	Является ли символ разделителем: пробел, tab, и т.д.
	Символ в нижнем регистре — строчные буквы?
	Символ в верхнем регистре — заглавные буквы?
	Преобразует символ в нижний регистр
	Преобразует символ в верхний регистр

Особенностью данных методов является то, что они работают со всеми известными алфавитами: символы арабских цифр будут определяться как цифры и т.п.

Объявление и определение метода в Java

Методы могут возвращать или не возвращать значения, могут вызываться с указанием параметров или без. Тип возвращаемых данных указывают при объявлении метода — перед его именем.

В примере ниже метод должен найти большее из двух целых чисел, поэтому тип возвращаемого значения — int:

В заголовке метода сначала идут модификаторы, определяющие, на каких условиях он доступен для вызова. Об этом чуть ниже. Вернёмся к заголовку: int — возвращаемый тип, maxFinder — имя метода, в скобках — параметры.

В теле метода заводим переменную max, куда потом запишем большее число. Далее сравниваем значения, фиксируем большее в max и возвращаем.

Обратите внимание, return может работать не только с одной переменной, но и с выражением. Если бы мы не сравнивали значения, а складывали, результат можно было бы вернуть без дополнительной внутренней переменной

В теле метода была бы всего одна строка:

Когда метод не должен ничего возвращать, тип возвращаемого значения указывают как void. А если методу для работы не нужны входные параметры, скобки оставляют пустыми:

Структуры данных

Комбинирование хеш-таблиц

Комбинирование двух хеш-таблиц вручную через цикл очень неэффективно. Вот альтернативное решение этой проблемы, которое вам возможно понравится:

Array или ArrayList?

Выбор между и зависит от специфики задачи Java, которую вы хотите решить. Запомните следующие особенности этих типов:

• Массив имеет фиксированный размер, и память для него выделяется во время объявления, а размер может динамически меняться.
• Массивы Java работают намного быстрее, а в намного проще добавлять и удалять элементы.
• При работе с скорее всего возникнет ошибка .
• может быть только одномерным, когда массивы Java могут быть многомерными.

Битовые операции

Битовые операции в Java используются редко, но знать их нужно. Работают они так же, как и в Javascript.

Битовые операции в Java:

• Битовый сдвиг влево
  <<
• Битовый знаковый сдвиг вправо
  >>
• Беззнаковый битовый сдвиг вправо
  >>>. Он отличается от
  >>  тем, что ставит 0 в самую левую позицию, а
  >>  ставит то, что было в знаковом бите.
• Инвертация бит
  ~  меняет 0 на 1 и 1 на 0 во всех битах.
• Битовый 
  &  применяет побитовую операцию И
• Битовый
  |  применяет побитовую операцию ИЛИ
• Битовый
  ^  применяет XOR (исключающее или)

Эти операнды работают так же, как и из аналоги в других языках программирования. Вряд ли имеет смысл их особенно сильно рассматривать.

Main.java

Java

class Main {
public static void main(String[] args) {
int n1 = 4; // 100 в двоичной системе
System.out.println(«n1 >> 1 = » + (n1 >> 1)); //2 или 10
// в двоичной системе.

System.out.println(«n1 << 1 = » + (n1 << 1)); ;// 8 или 100
// в двоичной системе.

System.out.println(«0b101 & 0b100 = » + (0b101 & 0b100)); // 4 (0b100)
System.out.println(«0b001 | 0b100 = » + (0b001 | 0b100)); // 5 (0b101)
System.out.println(«0b1110 ^ 0b1011 = » + (0b1110 ^ 0b1011)); //5 (0b101);

System.out.println(«-2 >> 1 = » + (-2 >> 1)); // -1 (единица со знака
// сдвинется вправо, так что знак не поменяется)

System.out.println(«-2 >>> 1= » + (-2 >>> 1)); // 2147483647 (сменит
// знак, так как левый бит заполнится нулём).

System.out.println(«~1 = » + ~1) ; // -2 (0b000…001
// превратится в 0b1111..10)

}
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

classMain{ publicstaticvoidmain(Stringargs){ intn1=4;// 100 в двоичной системе System.out.println(«n1 >> 1 = «+(n1>>1));//2 или 10 // в двоичной системе. System.out.println(«n1 << 1 = «+(n1<<1));;// 8 или 100 // в двоичной системе. System.out.println(«0b101 & 0b100 = «+(0b101&0b100));// 4  (0b100) System.out.println(«0b001 | 0b100 = «+(0b001|0b100));// 5  (0b101) System.out.println(«0b1110 ^ 0b1011 = «+(0b1110^0b1011));//5 (0b101); System.out.println(«-2 >> 1 = «+(-2>>1));// -1 (единица со знака // сдвинется вправо, так что знак не поменяется) System.out.println(«-2 >>> 1= «+(-2>>>1));// 2147483647 (сменит // знак, так как левый бит заполнится нулём). System.out.println(«~1 = «+~1);// -2 (0b000…001 // превратится в 0b1111..10) } }

Тригонометрические функции

Класс Java Math содержит набор тригонометрических функций. Эти функции могут вычислять значения, используемые в тригонометрии, такие как синус, косинус, тангенс и т. д.

Mathkpi

Константа Math.PI представляет собой двойное значение, значение которого очень близко к значению PI — математическому определению PI.

Math.sin()

Метод Math.sin() вычисляет значение синуса некоторого значения угла в радианах:

double sin = Math.sin(Math.PI);
System.out.println("sin = " + sin);

Math.cos()

Метод Math.cos() вычисляет значение косинуса некоторого значения угла в радианах:

double cos = Math.cos(Math.PI);
System.out.println("cos = " + cos);

Math.tan()

Метод Math.tan() вычисляет значение тангенса некоторого значения угла в радианах:

double tan = Math.tan(Math.PI);
System.out.println("tan = " + tan);

Math.asin()

Метод Math.asin() вычисляет значение синусоиды значения от 1 до -1:

double asin = Math.asin(1.0);
System.out.println("asin = " + asin);

Math.acos()

Метод Math.acos() вычисляет значение арккосинуса от 1 до -1:

double acos = Math.acos(1.0);
System.out.println("acos = " + acos);

Math.atan()

Метод Math.atan() вычисляет значение арктангенса для значения от 1 до -1:

double atan = Math.atan(1.0);
System.out.println("atan = " + atan);

Вот что говорит JavaDoc:

Если вам нужен этот метод, пожалуйста, прочитайте JavaDoc.

Math.sinh()

Метод Math.sinh() вычисляет значение гиперболического синуса значения между 1 и -1:

double sinh = Math.sinh(1.0);
System.out.println("sinh = " + sinh);

Math.cosh()

Метод Math.cosh() вычисляет значение гиперболического косинуса от 1 до -1:

double cosh = Math.cosh(1.0);
System.out.println("cosh = " + cosh);

Math.tanh()

Метод Math.tanh() вычисляет значение гиперболического тангенса значения от 1 до -1:

double tanh = Math.tanh(1.0);
System.out.println("tanh = " + tanh);

Math.toDegrees()

Метод Math.toDegrees() преобразует угол в радианах в градусы:

double degrees = Math.toDegrees(Math.PI);
System.out.println("degrees = " + degrees);

Math.toRadians()

Метод Math.toRadians() преобразует угол в градусах в радианы:

double radians = Math.toRadians(180);
System.out.println("radians = " + radians);

5 Интересный факт о strictfp

В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:

Создатели Java:

Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!

Создатели процессора Intel:

Ребята, мы улучшили наши процессоры? и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!

Ученые и все, кто занимается сверхточными расчетами:

Круто! Молодцы. Отличная новость.

Создатели Java:

Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.

Вот теперь все опять отлично! Не благодарите.

Ученые и все, кто занимается сверхточными расчетами:

Да вы там совсем охренели? А ну быстро вернули все как было!

Создатели Java:

Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!

Ученые и все, кто занимается сверхточными расчетами:

Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?

Создатели Java:

Гм. Что же вы сразу не сказали. Конечно, вернем.

Вернули возможность пользоваться всеми фичами крутых процессоров.

Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!

Присвоение с выполнением другой операции

Операции 
+= (сложение с присвоением),
-= (вычитание с присвоением), 
*= (умножение с присвоением),
/= (деление с присвоением),
%= (взятие остатка с присвоением),
&= (битовый И с присвоением),
^=  (битовое исключающее ИЛИ с присвоением),
|= (битовое ИЛИ с присвоением),
<<= (сдвиг влево с присвоением),
>>= (знаковый сдвиг вправо с присвоением),
>>>=  (беззнаковый сдвиг вправо с присвоением) позволяют сразу выполнить операции и присвоить результат другой переменной.

Они работают так:

Java

E1 compop E2

1	E1 compop E2

эквивалентно

Java

E1 = (T) E1 op E2;

1	E1=(T)E1 op E2;

, где
T  — это тип переменной
E1.

То есть
intx1+=x2 эквивалентно
intx1=(int)x1+x2.

Main.java

Java

class Main {
public static void main(String[] args) {
int x1 = 100;
byte x2 = 100;
int x3 = 100;

x1 += 300; // эквивалентно x1 = (int) x1 + 300;
x2 += 300; // эквивалентно x2 = (byte) x2 + 300;
x3 += 300.1; // эквивалентно x3 = (int) x3 + 300.1;

System.out.println(«x1=» + x1); // 400
System.out.println(«x2=» + x2); // -112
System.out.println(«x3=» + x3); // 400
}
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

classMain{ publicstaticvoidmain(Stringargs){ intx1=100; bytex2=100; intx3=100; x1+=300;// эквивалентно x1 = (int) x1 + 300; x2+=300;// эквивалентно x2 = (byte) x2 + 300;       x3+=300.1;// эквивалентно x3 = (int) x3 + 300.1; System.out.println(«x1=»+x1);// 400 System.out.println(«x2=»+x2);// -112 System.out.println(«x3=»+x3);// 400 } }

2 Папка src

В Java принято все классы одной программы хранить в одной папке (и ее подпапках). Такую папку обычно называют (сокращение от source).

Такая папка называется корнем проекта (source root), и все пути для пакетов считаются от нее. Примеры:

Папки	Имя пакета

Программисты в такой ситуации скажут что-то типа «у нас есть проект по имени , который расположен в папке » или «у нас есть проект по имени , который расположен в папке »

Лучше всегда класть классы в пакеты, а не в корень папки . Когда классов мало, это ещё не проблема, но когда классов много, очень легко запутаться. Поэтому всегда создавайте классы только в пакетах.

В Java принято давать классам и пакетам осмысленные имена. Многие компании выпускают свои библиотеки (набор классов) и, чтобы не было путаницы, называют пакеты этих классов по имени компании/сайта/проекта:

Имя пакета	Имя компании/проекта
	Проект «Apache»
	Компания «Oracle»
	Компания Oracle, проект Java
	Компания «IBM», проект WebSphere
	Проект «Jboss»

Гиперболические тригонометрические функции

Гиперболические тригонометрические функции имеют такое же отношение к гиперболам, как обычные тригонометрические функции к окружностям. Представьте себе, что значения этих функций нанесены на Декартову плоскость для всех возможных значений аргумента t.

x = r cos(t)
y = r sin(t)

В результате у вас получится окружность радиуса r. Теперь представьте, что вместо обычных синуса и косинуса используются функции sinh и cosh.

x = r cosh(t)
y = r sinh(t)

В этом случае вы нарисуете равнобочную гиперболу, в которой точкой, наиболее близкой к началу координат, является r.

О гиперболических функциях можно рассуждать следующим образом: известно, что sin(x) равен (eix — e-ix, а cos(x) = (eix + e-ix)/2. Функции sinh и cosh можно получить, убрав мнимую единицу из этих формул, т.е. sinh(x) = (ex — e-x)/2, а cosh(x) = (ex + e-x)/2.

В Java 5 были добавлены все три метода: , и . При этом в состав класса пока не были включены обратные гиперболические функции: acosh, asinh и atanh.

График функции cosh(z) имеет вид свисающего каната, закрепленного с обоих концов. Он известен под именем цепная линия (catenary). В листинге 5 показан текст простой программы, рисующей цепную линию при помощи функции .

Листинг 5. Рисование цепной линии при помощи функции

import java.awt.*;

public class Catenary extends Frame {

    private static final int WIDTH = 200;
    private static final int HEIGHT = 200;
    private static final double MIN_X = -3.0;
    private static final double MAX_X = 3.0;
    private static final double MAX_Y = 8.0;

    private Polygon catenary = new Polygon();

    public Catenary(String title) {
        super(title);
        setSize(WIDTH, HEIGHT);
        for (double x = MIN_X; x <= MAX_X; x += 0.1) {
            double y = Math.cosh(x);
            int scaledX = (int) (x * WIDTH/(MAX_X - MIN_X) + WIDTH/2.0);
            int scaledY = (int) (y * HEIGHT/MAX_Y);
            // В компьютерной графике ось y направлена вниз, а не вверх
            // (как в Декартовых координатах), поэтому необходимо изменить знак
            scaledY = HEIGHT - scaledY;
            catenary.addPoint(scaledX, scaledY);
        }
    }

    public static void main(String[] args) {
        Frame f = new Catenary("Catenary");
        f.setVisible(true);
    }

    public void paint(Graphics g) {
        g.drawPolygon(catenary);
    }

}

График показан на рисунке 1.

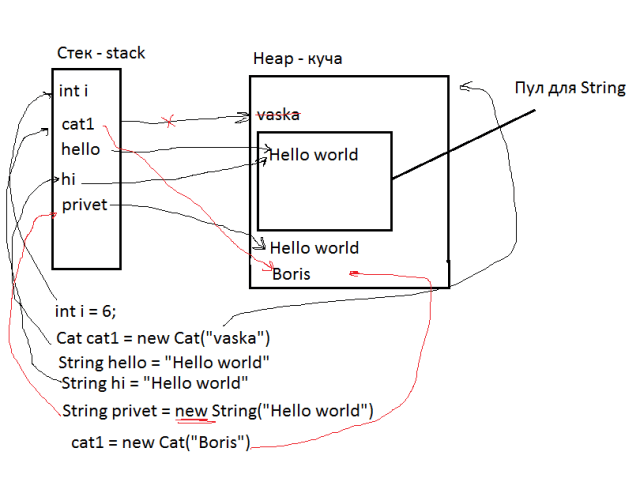
2 Устройство чисел с плавающей точкой

Тип может хранить значения в диапазоне до . Такой гигантский диапазон значений (по сравнению с типом ) объясняется тем, что тип (как и ) устроен совсем иначе по сравнению с целыми типами. Каждая переменная типа содержит два числа: первое называется мантисса, а второе — степень.

Допустим, у нас есть число , и мы сохранили его в переменную типа . Тогда число будет преобразовано к виду , и внутри типа будут храниться два числа — и . Красным выделена «значащая часть числа» (манти́сса), синим — степень.

Такой подход позволяет хранить как очень большие числа, так и очень маленькие. Но т.к. размер числа ограничен 8 байтами (64 бита) и часть бит используется под хранение
степени (а также знака числа и знака степени), максимальная длина
мантиссы ограничена 15 цифрами.

4 Минимум и максимум из нескольких чисел

Есть еще одно полезное применение функций и .

Это вычисление минимума (или максимума) из нескольких чисел или переменных. Функции очень удобно вызывать друг в друге.

Вот как можно записать минимум из 3-х чисел:

А что? Очень удобно: вычисляем минимум пары чисел, а затем возвращаем меньшее число из найденного и оставшегося.

Минимум из четырех чисел получается аналогично:

Хотя можно эту формулу записать немного понятнее:

Для функции все аналогично.

Использование оператора или тернарного оператора сделало бы эти записи немного более громоздкими. А использование функций и — просто идеальное решение.

Приоритеты операций

Все операции вычисляются слева направо (сначала вычисляется левый операнд, затем правый и затем сама операций, кроме операции присваивания. Операция присваивания вычисляется справа налево.

Вычисления производятся в соответствии с таблицей приоритетов операций, приведённой ниже. Операция, находящаяся выше в таблице, имеет более высокий приоритет, чем операция, находящаяся ниже, и вычиляется раньше. Операции, находящиеся на одной строке, имеют одинаковый приоритет. Если в одном выражении находится несколько разных операций, то сначала вычисляется результат операции с наивысшим приоритетом. Можно использовать скобки для указания того, что сначала нужно вычислить эту часть выражения.

Пример 1:

Java

int z = 200 * (3 + 4);

1	intz=200*(3+4);

Последовательность вычисляения такая:

1. 3+4 = 7
2. 200 * 7 = 1 400
3. z = 1 400

Пример 2:

Java

int x;
int y;
int z = x = y = 10000 + 20000 >> 1 + 3 * 2;

1 2 3

intx; inty; intz=x=y=10000+20000>>1+3*2;

Последовательность вычисления такая:

1. 10 000 + 20 000 = 30 000 (Присвоение вычисляется справа налево, поэтому сначала смотрится
   y=10000+20000>>1+3*2 , и вычисляется правая часть. В правой части (
   10000+20000>>1+3*2 ) вычисление идёт слева направо, и берётся
   10000+20000 (выбирается среди
   10000+20000 ,
   20000>>1 ,
   1+3  и
   3*2 ), которое вычисляется перед сдвигом, так как у сложения приоритет выше.)
2. 3 * 2 = 6 (В выражении
   30000>>1+3*2 вычисление идёт слева направо, и выбирается умножение(среди
   30000>>1 ,
   1+3  и
   3*2 ), так как у него приоритет выше, что означает, что сложение будет выполнено раньше.)
3. 1 + 6 = 7 (В выражении
   30000>>1+6 вычисление идёт слева направо и сложение вычисляется раньше сдвига, так как приоритет у сложения выше.)
4. 30 000 >> 7 = 234   (0b00…111010100110000 сдвигаем на 7 бит вправо и получаем 0b00…0011101010)
5. y = 234
6. x = 234
7. z = 234

Таблица приоритетов операций

Группа операций	Приоритет
Группировка
Доступ к члену
постфиксные
унарные
мультипликативные
аддитивные
сдвиги
сравнения
равенства
бинарный И
бинарный исключающее ИЛИ
бинарный ИЛИ
логический И
логический ИЛИ
тернарный
лямбда
присваивания

Цикл статей «Учебник Java 8».

Следующая статья — «Java 8 выражения, инструкции и блоки».
Предыдущая статья — «Переменные в Java 8».