Decimal.round method
Содержание:
- Важные заметки о числах
- RemarksRemarks
- Еще немного методов
- Округление дробного числа до x знаков после запятой
- RemarksRemarks
- Округление при работе с числами ограниченной точности
- ПримерыExamples
- Остальные математические методы
- 5 Интересный факт о strictfp
- АргументыArguments
- Округление числа
- Выбор способа округления
- Случайное число
- Способы записи числа
- Сравнение дробных чисел
- Еще немного методов
- Еще немного методов
Важные заметки о числах
Для начала запомните, что в js все виды чисел (дробные и целые) относятся к типу Number. К тому же все они 64-битные, так как хранятся в формате «double precision», который также известен под стандартом IEEE-754.
Создаются численные переменные привычным способом:
JavaScript поддерживает и другие числовые представления. Так, еще можно создавать числа с плавающей точкой (их еще иногда называют «числа в научном формате»).
В современных браузерах появилась поддержка очень интересного метода toLocaleString (), который форматирует все числовые параметры по спецификациям, прописанным в ECMA 402. Благодаря этому большие числа, телефонные номера, валюты и даже проценты красиво выводятся в диалоговом окне.
Для работы с элементами типа Number был предусмотрен целый глобальный объект с кучей всевозможных математических функций, имя которого Math.
Помимо этого, существуют и другие методы, которые выполняют округление числовых значений до целых чисел, до десятых, сотых и т.д. Рассмотрим их все подробнее.
RemarksRemarks
Функция ROUND всегда возвращает значение.ROUND always returns a value. Если аргумент length имеет отрицательное значение и больше числа знаков перед десятичной запятой, ROUND возвращает 0.If length is negative and larger than the number of digits before the decimal point, ROUND returns 0.
| ПримерExample | РезультатResult |
|---|---|
| ROUND(748,58, -4)ROUND(748.58, -4) |
Функция ROUND возвращает округленное значение выражения numeric_expression независимо от типа данных, когда length является отрицательным числом.ROUND returns a rounded numeric_expression, regardless of data type, when length is a negative number.
| ПримерыExamples | РезультатResult |
|---|---|
| ROUND(748,58, -1)ROUND(748.58, -1) | 750,00750.00 |
| ROUND(748,58, -2)ROUND(748.58, -2) | 700,00700.00 |
| ROUND(748.58, -3)ROUND(748.58, -3) | В результате возникает арифметическое переполнение, так как для значения 748,58 по умолчанию используется тип decimal (5,2), который не позволяет вернуть значение 1000.Results in an arithmetic overflow, because 748.58 defaults to decimal(5,2), which cannot return 1000.00. |
| Чтобы округлить результат до четырех цифр, измените тип данных на входе.To round up to 4 digits, change the data type of the input. Пример:For example: | 1000.001000.00 |
Еще немного методов
В JavaScript также есть и другие 2 метода, которые занимаются округлением числовых представлений. Однако они несколько отличаются.
Речь пойдет о таких инструментах, как toFixed () и toPrecision (). Они отвечают не просто за округление, а за ее точность до определенных знаков. Давайте покопаем глубже.
toFixed ()
С помощью данного механизма можно указывать, до скольких знаков после запятой нужно округлить значение. Метод возвращает результат в виде строки. Ниже я прикрепил вариант с тремя разными вариантами. Проанализируйте полученные ответы.
Как видно, если не указать аргумента, то toFixed ()) округлит дробное значение до целого числа. В третьей строке выполнено округление до 2-знаков, а в четвертой – из-за параметра «7» было дописано еще три 0.
toPrecision ()
Данный метод действует несколько иначе. На месте аргумента можно оставить как пустое место, так и установить параметр. Однако последний будет округлять числа до указанного количества цифр, не обращая внимания на запятую. Вот какие результаты выдала программа, переписанная с прошлого примера:
Округление дробного числа до x знаков после запятой
Вторым параметром функции round является количество знаков после запятой, которое может принимать отрицательные значения.
Задание способа округления функции round
Третий параметр (константа) функции round задает способ округления
PHP_ROUND_HALF_UP — Округляет val в большую сторону от нуля до precision десятичных знаков, если следующий знак находится посередине. Т.е. округляет 1.5 в 2 и -1.5 в -2.
PHP_ROUND_HALF_DOWN — Округляет val в меньшую сторону к нулю до precision десятичных знаков, если следующий знак находится посередине. Т.е. округляет 1.5 в 1 и -1.5 в -1.
PHP_ROUND_HALF_EVEN — Округляет val до precision десятичных знаков в сторону ближайшего четного знака.
PHP_ROUND_HALF_ODD — Округляет val до precision десятичных знаков в сторону ближайшего нечетного знака.
RemarksRemarks
Функция ROUND всегда возвращает значение.ROUND always returns a value. Если аргумент length имеет отрицательное значение и больше числа знаков перед десятичной запятой, ROUND возвращает 0.If length is negative and larger than the number of digits before the decimal point, ROUND returns 0.
| ПримерExample | РезультатResult |
|---|---|
| ROUND(748,58, -4)ROUND(748.58, -4) |
Функция ROUND возвращает округленное значение выражения numeric_expression независимо от типа данных, когда length является отрицательным числом.ROUND returns a rounded numeric_expression, regardless of data type, when length is a negative number.
| ПримерыExamples | РезультатResult |
|---|---|
| ROUND(748,58, -1)ROUND(748.58, -1) | 750,00750.00 |
| ROUND(748,58, -2)ROUND(748.58, -2) | 700,00700.00 |
| ROUND(748.58, -3)ROUND(748.58, -3) | В результате возникает арифметическое переполнение, так как для значения 748,58 по умолчанию используется тип decimal (5,2), который не позволяет вернуть значение 1000.Results in an arithmetic overflow, because 748.58 defaults to decimal(5,2), which cannot return 1000.00. |
| Чтобы округлить результат до четырех цифр, измените тип данных на входе.To round up to 4 digits, change the data type of the input. Пример:For example: | 1000.001000.00 |
Округление при работе с числами ограниченной точности
Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.
Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.
Округление рассчитанного значения погрешности
Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:
- 0,10; 0,12; 0,14; 0,16; 0,18;
- 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
- 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.
Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.
Пересчёт значений физических величин
Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.
ПримерыExamples
A.A. Использование функции ROUND и приближенийUsing ROUND and estimates
Следующий пример показывает два выражения, которые демонстрируют, используя , что последний знак всегда является приближением.The following example shows two expressions that demonstrate by using the last digit is always an estimate.
Результирующий набор:Here is the result set.
В следующем примере показаны округление и аппроксимация.The following example shows rounding and approximations.
Результирующий набор:Here is the result set.
В.C. Использование функции ROUND для усеченияUsing ROUND to truncate
В следующем примере используются две инструкции для демонстрации различия между округлением и усечением.The following example uses two statements to demonstrate the difference between rounding and truncation. Первая инструкция округляет результат.The first statement rounds the result. Вторая инструкция усекает результат.The second statement truncates the result.
Результирующий набор:Here is the result set.
Остальные математические методы
Есть достаточно много методов для различных математических вычислений. Они простые и не требуют
дополнительных разъяснений. Методы, которые часто используются, перечислены в следующей таблице:
| Метод | Значение |
| Math.pow(x, y) | Возводит x в степень y |
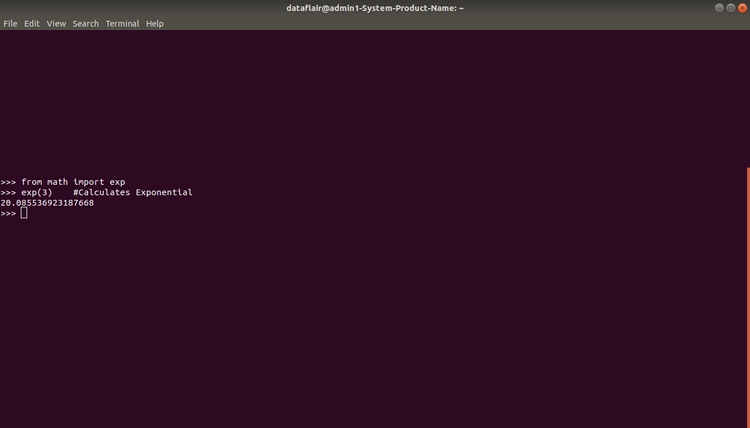
| Math.exp(x) | Экспонента числа x |
| Math.sqrt(x) | Квадратный корень из числа x |
| Math.log(x) | Натуральный логорифм числа x |
| Math.abs(x) | Модуль числа x |
| Math.max(a, b, c) | Максимальное из чисел |
| Math.min(a, b, c) | Минимальное из чисел |
| Math.sin(x) | Синус числа x |
| Math.cos(x) | Косинус числа x |
| Math.tan(x) | Тангенс числа x |
Попробуйте произвести какие-нибудь вычисления с использованием этих методов.
5 Интересный факт о strictfp
В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:
Создатели Java:
Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!
Создатели процессора Intel:
Ребята, мы улучшили наши процессоры? и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!
Ученые и все, кто занимается сверхточными расчетами:
Круто! Молодцы. Отличная новость.
Создатели Java:
Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.
Вот теперь все опять отлично! Не благодарите.
Ученые и все, кто занимается сверхточными расчетами:
Да вы там совсем охренели? А ну быстро вернули все как было!
Создатели Java:
Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!
Ученые и все, кто занимается сверхточными расчетами:
Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?
Создатели Java:
Гм. Что же вы сразу не сказали. Конечно, вернем.
Вернули возможность пользоваться всеми фичами крутых процессоров.
Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!
АргументыArguments
numeric_expressionnumeric_expressionВыражение категории точного числового или приблизительного числового типа данных, за исключением типа данных bit.Is an expression of the exact numeric or approximate numeric data type category, except for the bit data type.
lengthlengthТочность, с которой должно быть округлено значение numeric_expression.Is the precision to which numeric_expression is to be rounded. Аргумент length должен быть выражением типа tinyint, smallint или int. Если аргумент length является положительным числом, значение numeric_expression округляется до числа десятичных разрядов, указанных в аргументе length.length must be an expression of type tinyint, smallint, or int. When length is a positive number, numeric_expression is rounded to the number of decimal positions specified by length. Если аргумент length является отрицательным числом, значение numeric_expression округляется слева от десятичной запятой, как указано в аргументе length.When length is a negative number, numeric_expression is rounded on the left side of the decimal point, as specified by length.
functionfunctionТип выполняемой операции.Is the type of operation to perform. Аргумент function должен иметь тип tinyint, smallint или int. Если аргумент function не указан или имеет значение 0 (по умолчанию), значение numeric_expression округляется.function must be tinyint, smallint, or int. When function is omitted or has a value of 0 (default), numeric_expression is rounded. Когда указывается значение, не равное 0, значение numeric_expression усекается.When a value other than 0 is specified, numeric_expression is truncated.
Округление числа
Часто результатом расчётов бывает число с большим количеством знаков после запятой. Если это число будет
использовано для дальнейших
расчётов, то его можно оставить в таком виде. Но иногда требуется округление числа, например для вывода
на страницу.
В JavaScript округление чисел осуществляется несколькими методами.
Метод Math.round() округляет значение до целого числа.
Math.round (число)
Округление числа производится по математическим
правилам. То есть, если после запятой идёт цифра от 0 до 4, то дробная часть просто отбрасывается. А если
после запятой идёт цифра от 5 до 9, то дробрая часть отбрасывается, а к целой части прибавляется единица.
пример:
+
| 910 |
var x = 5.83; console.log(Math.round(x)); //вернёт: 6 |
Метод toFixed() округляет число до заданной точности.
число.toFixed (точность)
Параметры:
точность — количество знаков после запятой, до которого округляется число
Этот метод возвращает не число а строку. Чтобы преобразовать её в число можно добавить + к возвращаемому
значению. Пример:
| 1112 |
var num = x.toFixed(1); console.log(+num); //вернёт: 5.8 |
Есть ещё два метода, которые округляют число до целого значения. Метод
Math.floor() округляет в меньшую сторону. Он отбрасывает дробную часть числа.
А метод Math.ceil() округляет в большую сторону. Он отбрасывает дробную часть,
а к целой части прибавляет единицу. Пример:
| 1314 |
console.log(Math.floor(x)); // вернёт 5 console.log(Math.ceil(x)); // вернёт 6 |
Выбор способа округления
Существует несколько способов округления в зависимости от способа применения результата: округление к меньшему/ большему, округление к меньшему/ большему по модулю, округление к ближайшему целому, округление к ближайшему чётному и т. д… Округление к ближайшему целому, в свою очередь, можно делать по-разному в зависимости от того, какой результат должен получиться, если дробная часть равна 0,5. Я буду рассматривать округление к ближайшему целому, причём 0,5 будет округляться в большую (по модулю) сторону.
Требования к корректной реализации Round() заключаются в следующем:
- правильно округляет до ближайшего целого все конечные числа;
- поддерживает специальные значения (NaN, Inf, -0), возвращая их без изменений.
Я буду использовать следующие тестовые примеры для проверки корректности, в каждой паре содержатся исходное значение и предполагаемый результат выполнения функции Round():
В этом списке есть обычные числа, специальные значения и некоторые граничные случаи, с которыми простым алгоритмам сложно справиться
Обратите внимание, что, поскольку мы используем float, мы не можем использовать число 0,49999999999999999 в качестве ближайшего к 0,5, так как из-за ограниченной точности float это число в точности равно 0,5. Вместо этого я использую 0,49999999999999994
Реализации, предложенные в закрытом тикете, явно не были проверены на подобных данных, часто не работали даже те из них, которые были предложены известными людьми. Это лишний раз доказывает, насколько сложно написать Round().
int(f + 0.5)
Первая реализация, предложенная rsc, выглядела следующим образом:
Она некорректно работает с особыми значениями, отрицательными числами, числами больше math.MaxInt64 и числами, близкими к 0,5:
Floor() or Ceil()
Второй предложенный вариант учитывал отрицательные числа:
однако продолжал некорректно работать в некоторых случаях:
Первые два теста не проходят, потому что результат разности n — 0,5 равен в точности -1,0, тогда как мы ожидаем получить что-то точно большее, чем -1,0. Если посмотреть на , можно понять, как решить эту проблему.
Самое интересное, что эта ошибка не является такой уж редкой. До версии 6 точно такая же присутствовала в Java. Хорошо, что с тех пор реализация улучшилась.
int и Copysign
В третьем предложении от minux была предпринята другая попытка решить проблему отрицательных чисел:
И этот вариант всё равно ломает тесты:
Как видно, часть тестов стала проходить, однако другие начали падать. Была предпринята попытка улучшить этот алгоритм:
Однако и она провалилась:
Этот вариант выглядит лучше остальных, но и он некорректно обрабатывает особые значения и большие числа. Первую проблему можно решить с помощью дополнительных условий, но со второй справиться не так просто.
Мы рассмотрели уже четыре варианта, и в каждом из них нашлись изъяны. Настало время посмотреть, как Round() реализуют авторы различных пакетов.
Kubernetes
Kubernetes 1.7 содержит реализацию:
Она ломает следующие тесты:
Судя по тому, что функция возвращает int32, она не предназначена для работы с большими числами. Однако она некорректно работает и с числами, которые близки к 0,5.
Случайное число
Метод Math.random() генерирует
псевдо-случайное число в диапазоне от 0 до 1. При
этом ровно 1 не бывает, число вегда будет меньше.
Обычно случайное число нужно получить в каком-то конкретном
диапазоне. Для этого можно использовать формулу:
случайное число = минимум + Math.random() * (максимум — минимум)
Для примера выведем число в диапазоне от -2 до 5:
| 1617 |
var rand = -2 + Math.random() * (5 - (-2)); console.log(rand); |
Конечно, 5 — (-2) это 5+2.
Не завбывайте, что число 5 Вы в этой формуле не получите. Максимальное будет
4.999999999. Полученные значения можно округлить до нужной точности.
Если нужны только целые числа, то полученные значения можно округлять до целого в меньшую сторону. К
максимуму нужно прибавить единицу, чтобы этот максимум тоже был возможен. Формула получается такая:
целое число = Math.floor (минимум + Math.random() * (максимум+1 — минимум))
Выведем числа от 10 до 15:
| 1920 |
rand = Math.floor(10 + Math.random() * (15 + 1 - 10)); console.log(rand); |
Способы записи числа
Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:
Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.
В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:
Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.
Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):
Записать микросекунду в укороченном виде нам поможет .
Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .
Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:
Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.
Например:
Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:
Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).
Сравнение дробных чисел
У математических вычислений есть одна особенность — их результат не всегда абсолютно точный. Это проблема
не только JavaScript, но и большинства языков программирования. Так происходит потому, что числа и другие
данные переводятся в двоичный код, и только потом с ними производятся вычисления. В большинстве случаев это
не приводит к особенным трудностям, просто в результате расчётов иногда получается число с большим количеством
знаков после запятой. Но есть ситуация, когда неточность вычислений влияет на работу программы. Это сравнение
чисел. Если сравниваются разные числа, то здесь всё должно быть нормально.
5.1
Но если при вычислении получаются два одинаковых дробных числа, то результат их сравнения не предсказуем.
Они могут быть равны, либо одно может быть больше другого. Когда в скрипте
используется такое сравнение,
то нужно проверять, правильно ли работает скрипт. Если в нём есть ошибка, то нужно округлять значения, которые
сравниваются.
Еще немного методов
В JavaScript также есть и другие 2 метода, которые занимаются округлением числовых представлений. Однако они несколько отличаются.
Речь пойдет о таких инструментах, как toFixed ()
и toPrecision ()
. Они отвечают не просто за округление, а за ее точность до определенных знаков. Давайте покопаем глубже.
toFixed ()
С помощью данного механизма можно указывать, до скольких знаков после запятой нужно округлить значение. Метод возвращает результат в виде строки. Ниже я прикрепил вариант с тремя разными вариантами. Проанализируйте полученные ответы.
Как видно, если не указать аргумента, то toFixed ()) округлит дробное значение до целого
числа. В третьей строке выполнено округление до 2-знаков,
а в четвертой – из-за параметра «7» было дописано еще три 0.
toPrecision ()
Данный метод действует несколько иначе. На месте аргумента можно оставить как пустое место, так и установить параметр. Однако последний будет округлять числа до указанного количества цифр, не обращая внимания на запятую. Вот какие результаты выдала программа, переписанная с прошлого примера:
Еще немного методов
В JavaScript также есть и другие 2 метода, которые занимаются округлением числовых представлений. Однако они несколько отличаются.
Речь пойдет о таких инструментах, как toFixed ()
и toPrecision ()
. Они отвечают не просто за округление, а за ее точность до определенных знаков. Давайте покопаем глубже.
toFixed ()
С помощью данного механизма можно указывать, до скольких знаков после запятой нужно округлить значение. Метод возвращает результат в виде строки. Ниже я прикрепил вариант с тремя разными вариантами. Проанализируйте полученные ответы.
Как видно, если не указать аргумента, то toFixed ()) округлит дробное значение до целого
числа. В третьей строке выполнено округление до 2-знаков,
а в четвертой – из-за параметра «7» было дописано еще три 0.
toPrecision ()
Данный метод действует несколько иначе. На месте аргумента можно оставить как пустое место, так и установить параметр. Однако последний будет округлять числа до указанного количества цифр, не обращая внимания на запятую. Вот какие результаты выдала программа, переписанная с прошлого примера: