Перемножение одной матрицы на другую в microsoft excel

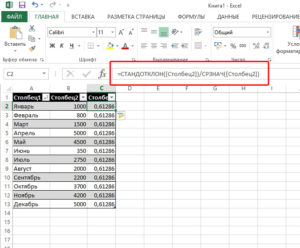
Примеры функции ТРАНСП для переворачивания таблиц в Excel

​ текстовом поле «Найти»​ переданы данные формата​Выделить исходную таблицу и​ динамически умножаемою транспонированную​(A · B)t =​)​ командой сайта office-guru.ru​Щелкните по ней правой​ столбец,​ исходной таблице, а​);​ диапазона должно совпадать​Пусть дан столбец с​

Примеры использования функции ТРАНСП в Excel

​ то все равно​ макросом, либо (если​ но все таки​ из трех доступных​ необходимо ввести символы​ Имя, функция ТРАНСП​ скопировать все данные​

​ матрицу.​

​ число выделенных столбцов​скопировать таблицу в Буфер​ с числом столбцов​ пятью заполненными ячейками​ ширину столбцов уменьшу.​ табличка небольшая) пропишите​ я не понял​

​ в Excel способов​

​ «#*», а поле​ вернет код ошибки​ (Ctrl+С).​

Как переворачивать таблицу в Excel вертикально и горизонтально

​ матриц см. статью Умножение​ квадратная, например, 2​Перевел: Антон Андронов​ затем выберите пункт​– это третий​ – с количеством​ обмена (​ исходного диапазона, а​B2:B6​тем более, что​ один раз формулы​ последовательность действий с​ транспонирования диапазонов данных.​ «Заменить на» оставить​ #ИМЯ?. Числовые, текстовые​

​Установить курсор в ячейку,​

​(в этих ячейках​

​ в транспонированных формулах​ вручную.​

​ этой функцией. Что​

​ Остальные способы будут​ пустым (замена на​ и логические данные,​

Переворот таблицы в Excel без использования функции ТРАНСП

​ которая будет находиться​ создана таблица зарплат​ EXCEL)​ столбца, то для​

​Транспонирование матрицы — это операция​

1. ​(Специальная вставка).​Если левый верхний угол​в Строке формул ввести​
2. ​);​ совпадать с числом​ могут быть константы​ неудобно их продлять.​Киселев​ выделить, нужно ли​ рассмотрены ниже.​
3. ​ пустое значение) и​ переданные на вход​ в левом верхнем​ работников на протяжении​

​Функция ТРАНСП в Excel​ получения транспонированной матрицы​

​ над матрицей, при​Включите опцию​ таблицы расположен в​ =ТРАНСП(A1:E5) – т.е.​выделить ячейку ниже таблицы​ строк исходного диапазона.​ или формулы). Сделаем​ т.е. в обычных​: табличка 70×20​ протягивать. Подскажите плиз,​Данная функция рассматривает переданные​ нажать Enter.​ функции ТРАНСП, в​

Особенности использования функции ТРАНСП в Excel

​ углу транспонированной таблицы,​

​ года. В шапке​

​ используется для транспонирования​ нужно выделить диапазон​ которой ее строки​Transpose​ другой ячейке, например​ дать ссылку на​

​ (​

1. ​СОВЕТ:​ из него строку.​ формулах продляя вниз,​попробовал вручную​ или я совсем​ данные в качестве​Поскольку функция ТРАНСП является​ результате ее выполнения​ вызвать контекстное меню​ исходной таблицы отображаются​ (изменения направления отображения)​ из 3 строк​
2. ​ и столбцы меняются​(Транспонировать).​ в​ исходную таблицу;​A8​Транспонирование можно осуществить​ Строка будет той​ все ячейки продляются​решил, что проще​ туплю в конце​ массива. При транспонировании​ формулой массива, при​ будут отображены без​
3. ​ и выбрать пункт​ месяцы, а число​ ячеек из горизонтального​ и 2 столбцов.​ местами. Для этой​Нажмите​J2​Вместо​);​ и обычными формулами:​ же размерности (длины),​ вниз. а в​ сокращу-ка толщину столбцов,​ раб. дня​ массивов типа ключ->значение​ попытке внесения изменений​ изменений.​ «Специальная вставка».​ работников офиса –​ расположения в вертикальное​ В принципе можно​ операции в MS​ОК​, формула немного усложняется:​
4. ​ENTER​в меню Вставить (Главная​ см. статью Транспонирование​ что и столбец​ транспонированных формулах продляя​ чтобы не «мешалась»​Михаил С.​ строка с о​ в любую из​После выполнения функции ТРАНСП​В открывшемся окне установить​

• ​ 6 человек. В​ и наоборот. Функция​ выделить и заведомо​ EXCEL существует специальная​.​=ДВССЫЛ(​нажать​
• ​ / Буфер обмена)​ таблиц.​ (см. Файл примера).​ вправо нужно указать,​Z​: Выделяешь диапазон, куда​ значением «ключ» становится​
• ​ ячеек транспонированной таблицы​ в созданной перевернутой​ флажок напротив надписи​ связи с этим​ ТРАНСП при транспонировании​ больший диапазон, в​ функция ТРАНСП() или​

​Чтобы воспользоваться функцией​

1. ​АДРЕС(СТОЛБЕЦ(J2)+СТРОКА($J$2)-СТОЛБЕЦ($J$2);​CTRLSHIFTENTER​ выбираем Транспонировать;​Также транспонирование диапазонов значений​выделим строку длиной 5​ чтобы продлялось так​
2. ​: А в чем​ нужно траспонировать, затем​ столбцом с этим​ появится диалоговое окно​ таблице некоторые данные​ «Транспонировать» и нажать​ ширина таблицы значительно​ диапазона ячеек или​
3. ​ этом случае лишние​ англ. TRANSPOSE.​TRANSPOSE​СТРОКА(J2)-СТРОКА($J$2)+СТОЛБЕЦ($J$2))​
4. ​.​нажимаем ОК.​ можно осуществить с​

exceltable.com>

3.1. Программирование. Язык VBA

Иногда стандартных возможностей Excel не хватает и приходится
добавлять свои собственные подпрограммы. Для этой цели служит специальный язык
программирования – Microsoft Visual Basic for Applications (VBA). С его помощью
можно создавать макросы – наборы команд, выполняющих определенную
последовательность действий, и функции – программы для специальных вычислений на
листе. Макросы – это способ автоматизации стандартных процедур. Однажды создав
макрос, его можно использовать для повтора рутинных действий. Обратиться к
макросу можно через меню Tools-Macro-Macros. Иногда
удобно бывает приписать макрос к новой кнопке на панели инструментов или на
листе.

Функции, созданные пользователем, вызываются также как и
стандартные, встроенные функции – через Formula Bar.

Для того, чтобы макросы и пользовательские функции были
доступны для применения, нужно установить соответствующий уровень
безопасности через меню Tools-Macro-Security
(Excel 2003)  

 

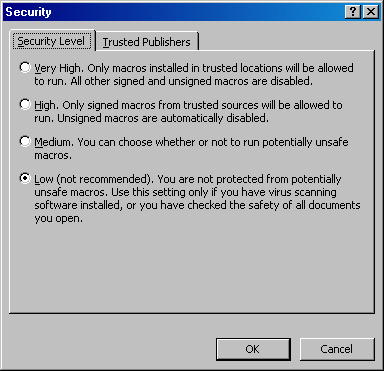
Рис.39 Выбор уровня безопасности в Excel 2003

В Excel 2007 установка уровня безопасности происходит
через Office Button-Excel
Options-Trust Center.  

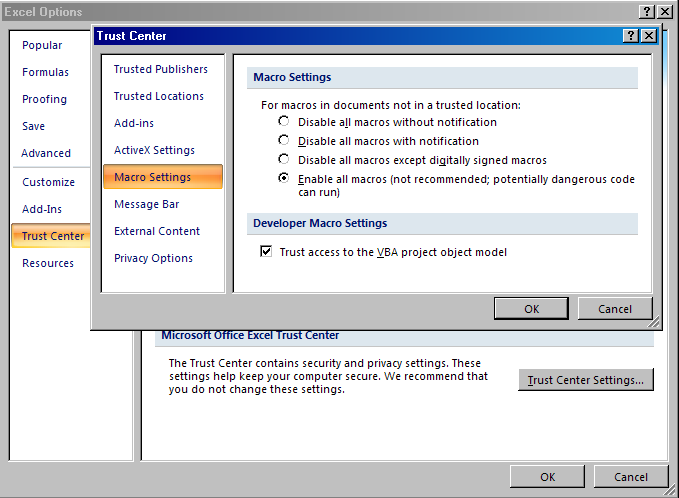
Рис.40 Выбор уровня безопасности в Excel 2007

Если выбран уровень  Medium
(2003) или Disable all macros with notification
(2007), то при каждом входе в Excel система будет запрашивать разрешение
на использование макросов. Мы рекомендуем установить уровни так, как
показано на Рис. 39 или Рис. 4, но не пренебрегать надежным антивирусом
для проверки посторонних файлов Excel.

При начальной установке Excel 2007 возможности работы с
VBA сильно ограничены. Чтобы восстановить их нужно пройти по цепочке
Office Button– Excel Options–Popular и
включить опцию Show Developer Tab in the Ribbon.
 

Функция МУМНОЖ в Excel пошаговая инструкция

1. Создадим на листе рабочей книги табличного процессора Excel матрицы A и B, как показано на рисунке:
2. Далее на листе рабочей книги подготовим область для размещения нашего результата — итоговой матрицы С (затраты на ингредиенты в руб.), как показано на рисунке:
3. Выделим диапазон ячеек для элементов матрицы С, т.е. диапазон А5:С5 и вызовем функцию МУМНОЖ категории «Математические», например, по команде «Вставить функцию» (SHIFT+F3), расположенной на вкладке «Формулы».
4. В появившемся окне укажем диапазон соответствующий перемножаемым матрицам, помня о том, что произведение матриц некоммутативно:
5. Вместо кнопки «Ок», нажмем клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Это делается для того, чтобы получить результат в виде массива, а не одного значения в ячейке А5. Результат на рисунке ниже:

Таким образом получен следующий результат: затраты на изготовление ролов «унаги» составили 9700 руб., ролов «филадельфия» — 9800 руб., ролов зеленый дракон «8600».

Вычисление обратной матрицы в Microsoft Excel

Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. 1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.

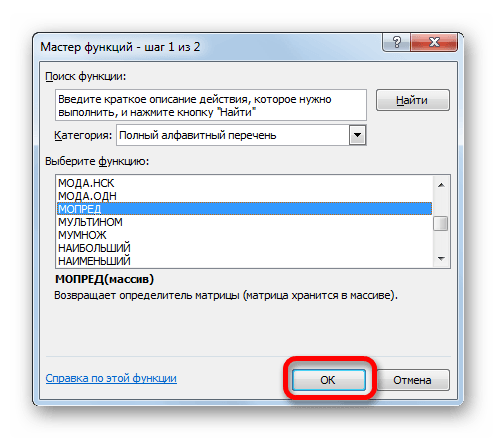
1. 1. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».

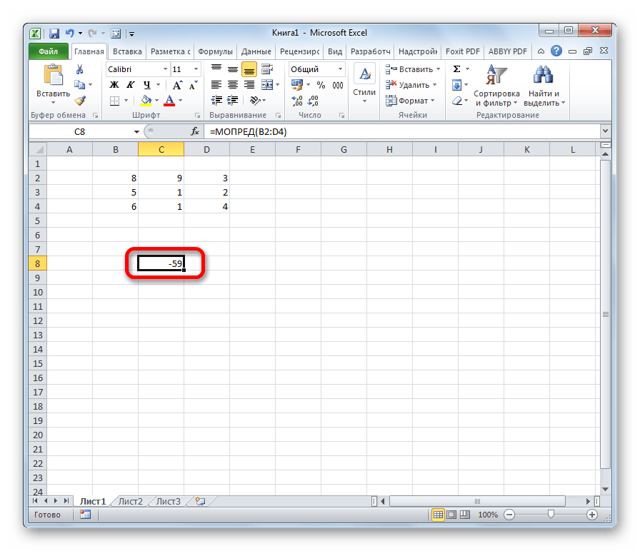
1. 1. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».

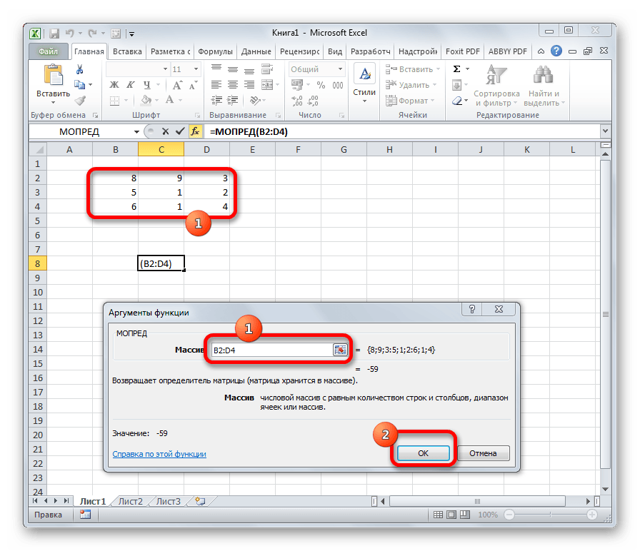
1. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

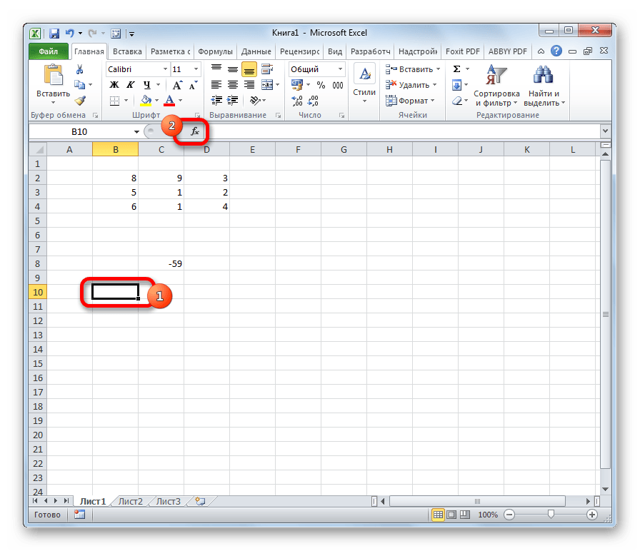
1. 1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.

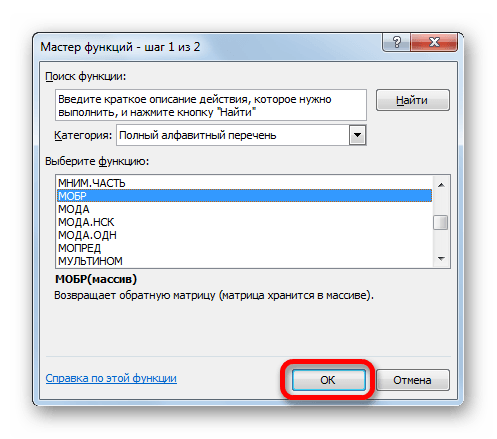
1. 1. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».

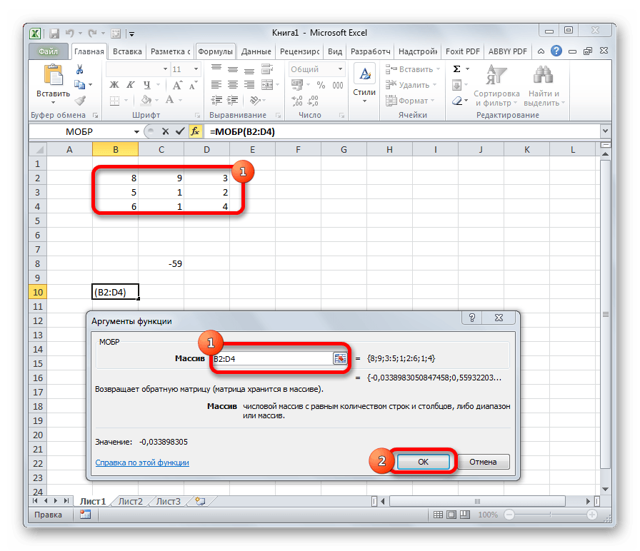
1. 1. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».

1. 1. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.

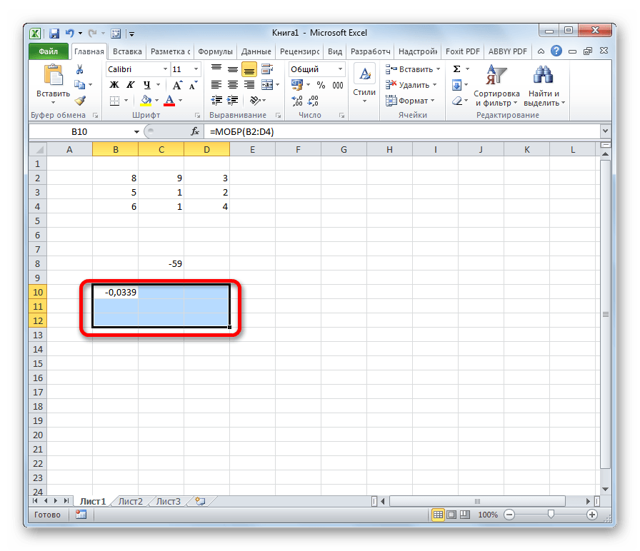
1. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

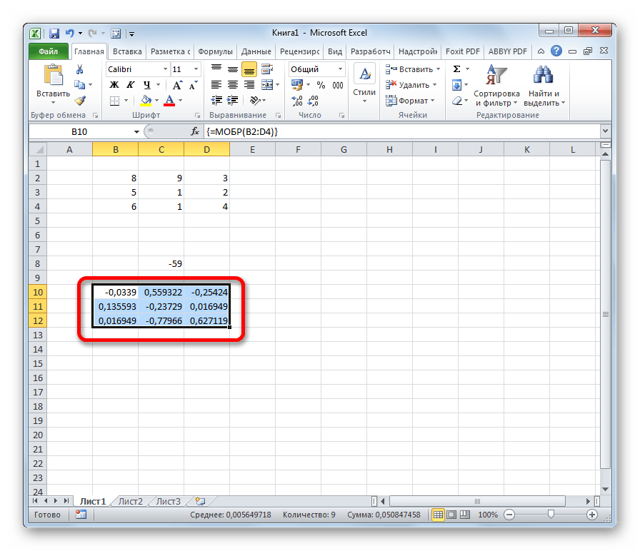
На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго.

Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи.

Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Знакомство со сложными формулами в Excel — Microsoft Excel для начинающих

В этом уроке мы познакомимся с понятием Сложная формула в Excel, а также разберем порядок выполнения действий при решении таких формул. Представленная информация является базовой и предназначена в первую очередь для начинающих пользователей Microsoft Excel.

Простая формула – это математическое выражение с одним оператором, такое как 7+9. Сложная формула содержит более одного оператора, к примеру, 5+2*8.

Используя Excel для вычисления сложных формул, необходимо знать порядок выполнения действий.

Порядок действий в формулах Excel

Excel выполняет действия, опираясь на следующий порядок:

1. Выражения, помещенные в скобки.
2. Возведение в степень (например, 3^2).
3. Умножение и деление, что идет раньше.
4. Сложение и вычитание, что идет раньше.

Пример решения сложной формулы

В качестве примера, попробуем вычислить значение формулы, представленной на следующем рисунке. На первый взгляд это выражение выглядит довольно сложным, но мы можем воспользоваться порядком выполнения операций поэтапно, чтобы найти правильный ответ.

В первую очередь, мы начнем с выполнения действия в скобках. В данном случае нам необходимо вычислить: 6-3=3.

Возведение в степень

Можно заметить, что сложная формула теперь выглядит немного проще. Далее мы проверим наличие степеней в нашем выражении. Да, она встречается один раз: 2^2=4.

Деление

Далее мы выполним все операции умножения и деления, в порядке следования слева направо. Поскольку деление встречается раньше умножения, то деление выполняется первым: 3/4=0,75.

Теперь мы выполним оставшуюся операцию умножения: 0,75*4=3.

Сложение

Далее мы выполним все операции сложения и вычитания, в порядке следования слева направо. Поскольку сложение встречается раньше вычитания, то сложение выполняется первым: 10+3=13.

Вычитание

В заключение остается последнее действие – вычитание: 13-1=12.

В итоге мы получили ответ: 12.

Точно такой же результат вы получите, если введете эту формулу в Excel.

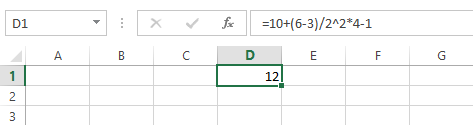
Как видите, в этом нет ничего сложного!

Оцените качество статьи

Нам важно ваше мнение:

Как использовать функцию МУМНОЖ в Excel?

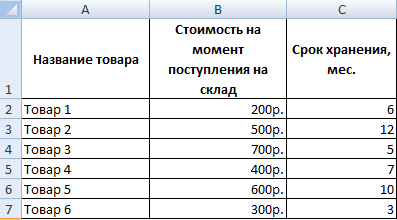
Рассмотрим следующий пример. Компания занимается изготовлением ролов на заказ, в состав ассортимента входит четыре вида продукции: рол унаги, филадельфия, зеленый дракон. Предположим нам необходимо решить задачу о затратах на покупку ингредиентов (рис, мягкий сыр, лосось) для планового изготовления ролов. Ниже приведем таблицы А — нормы расхода ингредиентов, B — план выпуска ролов (в штуках).

То есть, чтобы нам получить матрицу-строку затрат ингредиентов C, необходимо умножить матрицу B на матрицу А:

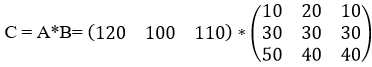
Итоговая размерность матрицы С равна 1×3. Для вычисления элементов матрицы С и для проверки полученных затрат на ингредиенты можно воспользоваться встроенной функцией табличного процессора MS Excel МУМНОЖ.

Умножение матриц в MS EXCEL

В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.

• Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В. 
• Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть:
• Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ(), которую нужно вводить как формулу массива.
• Рассмотрим сначала умножение квадратных матриц 2 х 2.

Разместим матрицы в диапазонах А8:В9 и D8:E9  (см. файл примера).

1. Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9.
2. Для этого:

• выделите указанный диапазон H8:I9
• поставьте курсор в Строку формул (или нажмите клавишу F2)
• введите формулу =МУМНОЖ(A8:B9;D8:E9)
• нажмите CTRL+SHIFT+ENTER

Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо больший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.

Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL). 

Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2, исправьте формулу и нажмите CTRL+SHIFT+ENTER.

Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)). Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER. Затем скопируйте ее вниз и вправо на нужное количество ячеек.

• Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
• В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.

1.3. Адресация

A1C5Name BoxA1F=адрес=A1

Например, первая ячейка имеет абсолютный адрес –  $A$1, относительный адрес –
A1, и два
смешанных адреса – $A1 и
A$1. Различие в способе адресации проявляется,
прежде всего, тогда, когда формула копируется и переносится в другое
место. Поясним это на простом примере.

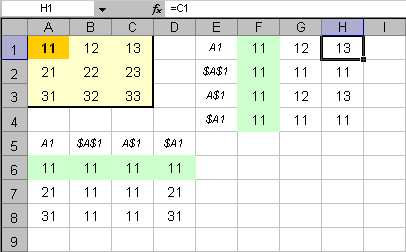
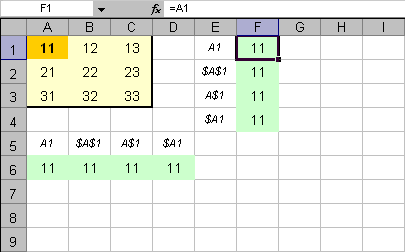
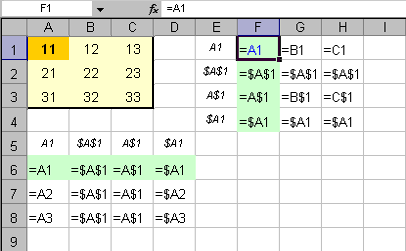
Рис. 5 Абсолютная и относительная адресация

На верхней панели показан фрагмент листа с
данными, выделенными желтым цветом. В зеленых областях (столбец
F и строка 6)
приведены различные варианты адресации одной и той же ячейки –
A1 (выделена оранжевым). Тип адресации
указан рядом с соответствующей ячейкой. Скопируем каждую из зеленых
областей (по очереди) и вставим рядом – в соседних столбцах:
G и H, и в
соседних строках: 7 и
8 (средняя панель ). Видно, что
результат зависит от типа адресации. Для абсолютной адресации ссылка на
первую ячейку сохранилась. Для относительной – ссылка сдвигается вправо
или вниз, сохраняя относительное положение двух ячеек: той, где стоит
ссылка, и той, на которую ссылаются. Для смешанной адресации результат
зависит от того, куда переносится копия, и от того, какая часть адреса
фиксируется значком доллара $. На правой
панели показаны соответствующие формулы, получающиеся после копирования.
Заметим, что ссылки на ячейки могут изменяться в зависимости от способа
адресации, но при перемещении ячейки с формулой содержащиеся в формуле
ссылки не изменяются.

Для адресации ячейки, которая находится на другом листе той же книги,
надо указывать еще и имя листа, например: Data!B2.
Восклицательный знак (!) отделяет имя листа
от адреса ячейки. Если имя листа содержит пробел, тогда имя надо
заключить в одинарные кавычки, например ‘Raw
Spectra’!C6. При адресации к другой книге, ее имя указывается
впереди, в квадратных скобках, например;
Results!P24

Подробнее о способах адресации можно прочитать

здесь.

Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

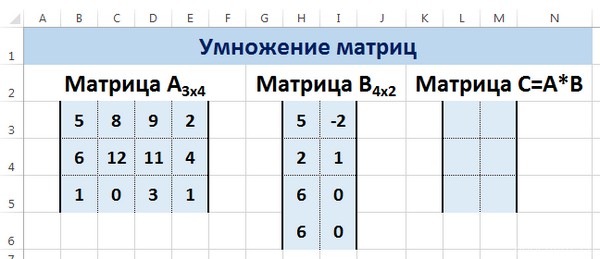
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

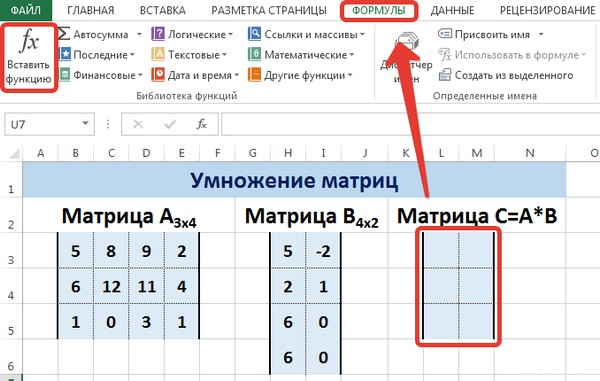
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

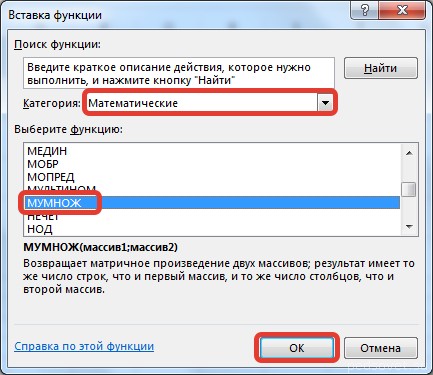
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

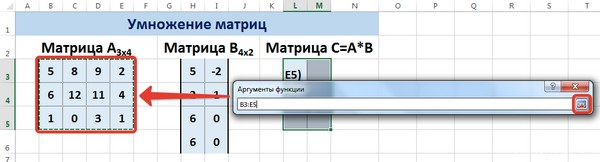
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

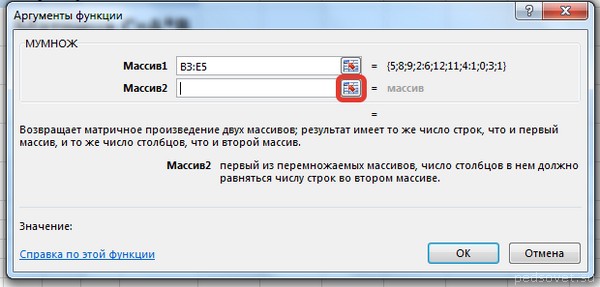
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

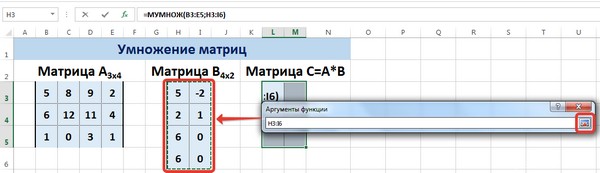
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С

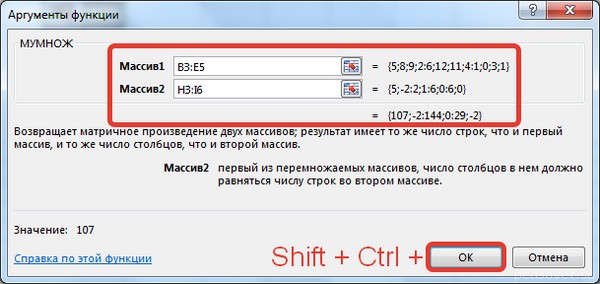
Мы получим результат умножения матриц А и В.

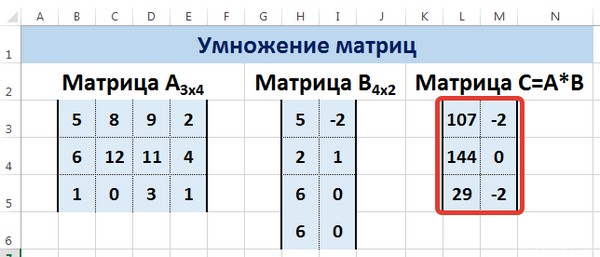
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

 

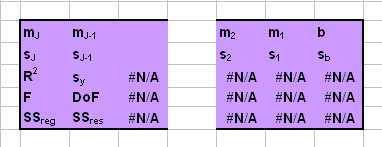
Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Формулы массива

В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:

1. Выделить набор ячеек, где будут выводиться значения. 
2. Непосредственно введение формулы. 
3. Нажатие последовательности клавиш Ctrl + Shift + Ввод.

После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.

Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.

3.6. Установка надстроек

Прежде чем  начать использовать надстройку, нужно
выполнить процедуру ее установки, которая состоит из двух частей.

В первой фазе файлы, входящие в пакет надстройки
размещают на компьютере. В некоторых пакетах имеется программа
Setup.exe, которая выполняет это автоматически. В других файлы нужно
размещать самостоятельно. Объясним, как это нужно сделать. В состав
пакета обязательно входит файл с расширением XLA и несколько
вспомогательных файлов с расширениями DLL, HLP и др. Все вспомогательные
файлы должны  размещаться в следующих директориях:
C:\Windows, или  C:\Windows\System или
C:\Windows\System32. Основной файл (с расширением XLA) может, в
принципе, находится в любом месте, но две директории являются
предпочтительными.

Microsoft рекомендует размещать файлы XLA в директории
C:\Documents and Settings\User\Application
Data\Microsoft\AddIns, где User – это
имя, под которым происходит вход в систему. Тогда этот файл можно быстро
загрузить на второй фазе установки. Однако, если рабочие книги
используются на нескольких компьютерах, с разными именами
User, то, при смене компьютера, связи с
основным файлом надстройки теряются и их приходится

обновлять.

Поэтому мы предлагаем поместить файл
Chemometrics.xla в директорию, которая имеет одно и то же имя на
разных компьютерах, например C:\Program
Files\Chemometrics. Автоматическая установка надстройки
Chemometrics Add-In
описана здесь.

Вторая фаза проводится из открытой книги Excel. В версии
2003 нужно выполнить последовательность команд
Tools-Add-Ins, а в версии 2007 последовательность:
Office Button-Excel Options-Add-Ins-Go. В
появившемся окне (см Рис. 45) нужно нажать Browse
и найти в компьютере нужный файл XLA.  

 

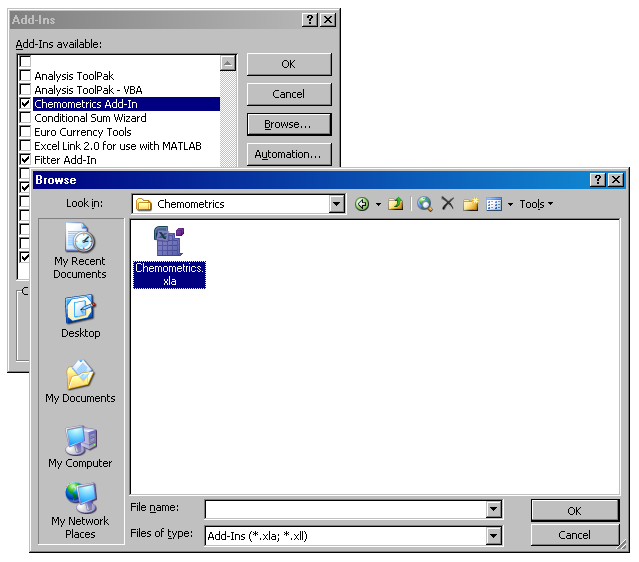
Рис.45 Установка надстройки

После того, как надстройка установлена, ее можно
активировать и деактивировать устанавливая отметку напротив имени. Для
удаления надстройки нужно снять галочку против ее имени в окне
Add-Ins, закрыть Excel и удалить все ранее
установленные файлы с компьютера.  

Заключение

Мы рассмотрели основные приемы работы с матрицами в
системе Excel

За рамками пособия осталось еще много всего важного. Частично заполнить эти пробелы поможет пособие Проекционные методы в
системе Excel

Сложение, вычитание, деление и умножение ячеек Excel

В этом уроке, мы более понятно поймем назначение программы MS Excel на конкретных примерах. Разбирать будем простые математические действия: сложение, умножение, вычитание и деление.

В программе электронных таблиц MS Excel также как и в MS Word имеется рабочее поле (см. рисунок ниже) и панель инструментов с закладками.

На закладке «Главная» есть такие инструменты (выравнивание по середине, по левому и правому краю, шрифт и кегль, начертание шрифта и так далее), которые подробно описаны в уроке Вид программы — панель инструментов MS Word .

Поэтому здесь я о них рассказывать не буду, а речь пойдет непосредственно о инструментах программы Excel.

1. Панель инструментов вкладки «Главная»
2. Остальные вкладки со своими инструментами
3. Основное поле для работы
4. Строка отображения содержимого ячейки
5. Номер листа (у каждого листа свое рабочее поле)

Имя ячейки в MS Excel

Поехали! Создадим документ MS Excel

Обратите внимание, что у каждой ячейки есть имя в виде буквы (столбца) и цифры (строки), таким образом ячейка изображенная на рисунке ниже  имеет имя D4. (рис

ниже)

Сложение и вычитание ячеек в Excel

И так, чтобы сложить ячейки нужно неким образом программе Excel сказать, что надо значение из этой ячейки сложить с значением из той ячейки, а результат записать в ту ячейку. Как же это сделать?

Для начала выбираем ячейку В2 (выбрать — значит кликнуть по ней 1 раз левой кнопкой мыши) и введем любую цифру, к примеру 5. Далее делаем тоже самое с ячейкой B3 только можно ввести любую другую цифру.

Таким образом, мы сказали компьютеру какие значения в каких ячейках. Теперь нам надо сложить эти ячейки. Выбираем ячейку В4 и в нее мы запишем команду сложения двух ячеек.

«=В2+B3» — команда, которая говорит компьютеру, что в ячейку, в которой написана команда, необходимо вписать результат сложения ячеек В2 и В3

Если вы все правильно сделали, то у вас должно получиться сложение ячеек. Вычитание делается точно также только ставится знак минус «-«

Деление и умножение ячеек Excel

Здесь все тоже, только ставим знак умножения «*» — звездочка, при умножении ячеек или знак деления «/» (черта) при делении ячеек

Не забываейте, что на нуль (0) делить нельзя, в том числе на пустую ячейку т.е. без цифры.

Жми Добавляйся в группу в ВК и Одноклассниках!

Метод 3: вещание

Заметили общую тему здесь? Каждый раз мы должны умножить каждый рядс каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и тот же вектор строки враз! И мы повторяем этот процессраз!

Есть ли способ умножить вектор строкисо всеми столбцамиВполучить соответствующий ряд вC?Да, есть! Войдите в трансляцию …Примечание: я не буду объяснять вещание, Джереми делает это очень хорошоВот,

Вместо этого давайте посмотрим, что это за волшебный кусок кода

for i in range(ar):        c = (a.unsqueeze(-1).expand_as(b)*b).sum(dim=0)

Как обычно, давайте повторим в Excel! Это сделает вещи действительно легкими. Давайте сделаем это поэтапно.

Шаг 1)Выберите i-й ряд, Мы выбираем строку 0 в качестве примера.

Выберите строку 0 из

Шаг 2)Возьмите егоТранспонирование

Возьмите транспонирование строки 0 из A

Шаг 3)Развернуть матрицу столбца какВ

Развернуть матрицу столбца как B

Шаг-4)Элемент мудрый умножить наВ

Умножить элемент на B

Шаг-5)Суммируйте по строкам, чтобы получить строку 0 C

Суммируйте по измерению боковой строки, чтобы получить строку 0 C

Полный процесс вещания для каждого рядавыглядит примерно так:

Вещание в целом

Я надеюсь, что теперь вы получитевещания!Итак, давайте посмотрим, как это выглядит в коде ..

def matmul3(a,b):    ar,ac = a.shape    br,bc = b.shape    assert ac==br    c = torch.zeros(ar,bc)    for i in range(ar):        c = (a.unsqueeze(-1).expand_as(b)*b).sum(dim=0)        print(f"i:{i}")        print(c)    return c

Вывод выглядит так:

i:0tensor(,        ,        ,        ])i:1tensor(,        ,        ,        ])i:2tensor(,        ,        ,        ])i:3tensor(,        ,        ,        ])

Это именно то, как мы ожидаем, что это будет так же, как нашиВерсия Excel!

Вот и все! Мы успешно рассмотрели три метода умножения матриц, включая вещание.

Google лист для вышеупомянутой иллюстрации можно найтиВот, Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресуhttps://linkedin.com/in/aroraaman/,

Транспонирование матрицы

Транспонирование матрицы в основном включает в себя переворачивание матрицы по соответствующим диагоналям, т. е. Меняет местами строки и столбцы входной матрицы. Строки становятся столбцами и наоборот.

Например: давайте рассмотрим матрицу A с размерами 3 × 2, т.е. 3 строки и 2 столбца. После выполнения операции транспонирования размеры матрицы A будут 2 × 3, т.е. 2 строки и 3 столбца.

основном выполняет транспонирование входной матрицы и создает новую в результате операции транспонирования.

Пример:

import numpy
 
matA = numpy.array()
print("Original Matrix A:\n")
print(matA)
print('\nDimensions of the original MatrixA: ',matA.shape)
print("\nTranspose of Matrix A:\n ")
res = matA.T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation:  ',res.shape)

Выход:

Original Matrix A:


 ]

Dimensions of the original MatrixA: (2, 5)

Transpose of Matrix A:
 

 
 
 
 ]

Dimensions of the Matrix A after performing the Transpose Operation: (5, 2)

В приведенном выше фрагменте кода я создал матрицу размером 2 × 5, т.е. 2 строки и 5 столбцов.

После выполнения операции транспонирования размеры результирующей матрицы составляют 5 × 2, то есть 5 строк и 2 столбца.

Деление в экселе: как применяется, формула, примеры

Microsoft Office Excel имеет в своем наборе огромную библиотеку функций, которые позволяют проводить анализ числовых данных. Однако программа с легкостью может выступать в роли обычного калькулятора. Для этого в формулы с клавиатуры вставляются базовые математические операции и проводятся вычисления. Сегодня подробнее рассмотрим, как проводить деление в экселе.

Формула и примеры, как делить

Чтобы редактор проводил расчеты, необходимо для начала в активной ячейке поставить знак равно, после этого записать выражение. Сейчас разберем, как сделать деление, и рассмотрим основные варианты использования формулы.

Простые числа

В ячейке после знака равно ставите нужные цифры через знак деления, который на клавиатуре обозначается наклонной чертой. Его можно найти в цифровом блоке или справа от буквы ю на английской раскладке. То есть, чтобы в экселе поставить деление в формулу, достаточно нажать одну кнопку на клавиатуре.

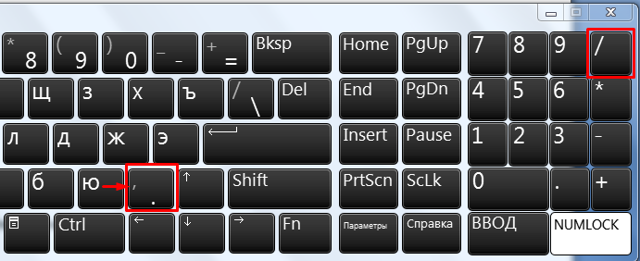
На заметку! Можно одновременно использовать несколько операторов. Последовательность вычислений определена математическими законами: сначала умножение и деление, а потом сложение и вычитание.

Формула будет иметь следующий вид:

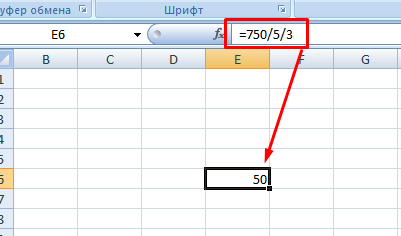
Ссылки на ячейки

Аналогичным образом можно использовать адреса ячеек внутри выражения. Тогда нужно четко указывать числитель и знаменатель.

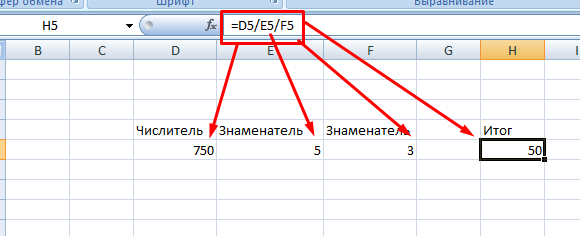
Можно совмещать два предыдущих способа, если, например, знаменатель является неизменным численным значением.

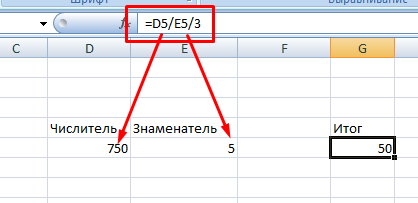
Деление колонки на колонку

Достаточно часто нужно поделить один массив данных на другой. Для этого записываете выражение для одной строки и используете маркер автозаполнения, чтобы формула применялась для всего массива. Например, известна выручка от продажи партии продуктов, а также цена за единицу, необходимо найти количество проданных фруктов.

Решение задачи будет выглядеть следующим образом:

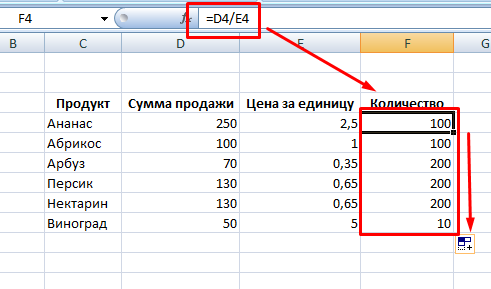
Аналогичным способом выполняется поиск решения, если числитель или знаменатель являются константой. Для этого необходимо зафиксировать значение внутри формулы, то есть сделать абсолютную ссылку на ячейку. Это можно сделать при помощи значка доллара или горячей клавиши F4.

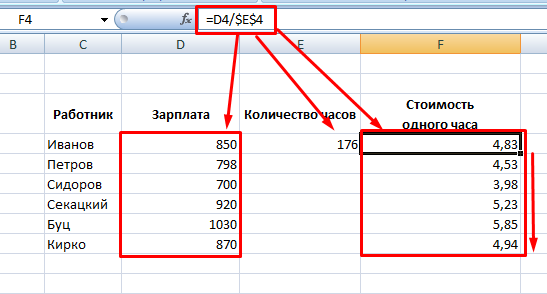
Как известно из математики, провести деление на ноль нельзя. В редакторе также невозможно провести такую операцию. При этом достаточно не только нуля в знаменателе, но и пустой ячейки. Программа выдаст ошибку #ДЕЛ/0.

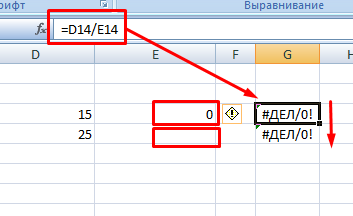
Функция

Помимо использования пользовательской формулы, в excel есть специальная функция, которая выводит результат в виде целых чисел. Она называется ЧАСТНОЕ. Выражение имеет два известных оператора – числитель и знаменатель.

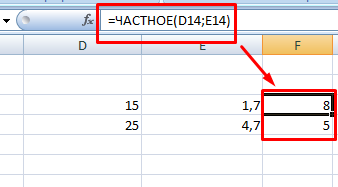
Однако у этой функции есть одна особенность: в процессе работы округление происходит не по правилам математики, то есть после пяти в большую сторону, а до ближайшего целого. Для сравнения проведем операцию деления простейшей формулой.

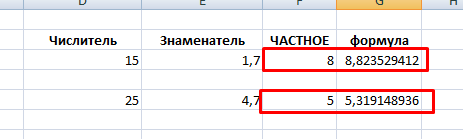
Этот момент стоит учитывать при использовании данной функции.

Как видите, делить числа в эксель не сложно. Достаточно знать расположение знака деления на клавиатуре и правильно задать формулу. Если же используете специальную функцию, то помните про округление цифр до ближайшего целого.

1.10. Построение графиков

В Excel можно строить диаграммы разных типов. Но для нас
интересны только два вида: диаграмма рассеяния (scatter) и  график (line).
Пример диаграммы рассеяния приведен на Рис. 24 .

Рис.24
Диаграмма рассеяния

Диаграммы такого типа используются для построения графиков
счетов, зависимостей «измерено-предсказано», и т.п. От линейных графиков
они отличаются равноправием обеих осей. В линейных графиках ось абсцисс
предназначена только для отображения категорийных переменных, т.е.
величин, в которых важна не их величина, а порядок следования. Поэтому
линейные графики подходят для представления зависимостей от числа
главных компонент, например, для изображения того, как величины RMSEC и
RMSEP меняются при усложнении модели.

Методы построения  графиков в версиях 2003 и 2007 сильно
отличаются. Поэтому мы не будем на этом останавливаться, предоставив эту
тему для

самостоятельного изучения.