Хеширование паролей в python: туториал по bcrypt с примерами

История

В январе 1953 года Ханс Петер Лун (нем. Hans Peter Luhn) (сотрудник фирмы IBM) предложил «хеш-кодирование». Дональд Кнут считает, что Ханс первым выдвинул систематическую идею «хеширования».

В 1956 году Арнольд Думи (англ. Arnold Dumey) в своей работе «Computers and automation» первым описал идею «хеширования» такой, какой её знает большинство программистов сейчас. Думи рассматривал «хеширование» как решение «проблемы словаря», предложил использовать в качестве «хеш-адреса» остаток от деления на простое число.

В 1957 году в журнале «IBM Journal of Research and Development» была опубликована статья Уэсли Питерсона (англ. W. Wesley Peterson) о поиске текста в больших файлах. Эта работа считается первой «серьёзной» работой по «хешированию». В статье Уэсли определил «открытую адресацию», указал на уменьшение производительности при удалении. Спустя шесть лет была опубликована работа Вернера Бухгольца (нем. Werner Buchholz), в которой было проведено обширное исследование «хеш-функций». В течение нескольких последующих лет «хеширование» широко использовалось, однако никаких значимых работ не публиковалось.

В 1967 году «хеширование» в современном значении упомянуто в книге Херберта Хеллермана «Принципы цифровых вычислительных систем». В 1968 году Роберт Моррис (англ. Robert Morris) опубликовал в журнале «Communications of the ACM» большой обзор по «хешированию». Эта работа считается «ключевой» публикацией, вводящей понятие о «хешировании» в научный оборот, и закрепившей термин «хеш», ранее применявшийся только специалистами (жаргон).

До начала 1990-х годов в русскоязычной литературе в качестве эквивалента термину «хеширование» благодаря работам Андрея Петровича Ершова использовалось слово «расстановка», а для «коллизий» использовался термин «конфликт» (А. П. Ершов использовал «расстановку» с 1956 года). В русскоязычном издании книги Никлауса Вирта «Алгоритмы и структуры данных» 1989 года также используется термин «расстановка». Предлагалось также назвать метод другим русским словом: «окрошка». Однако ни один из этих вариантов не прижился, и в русской литературе используется преимущественно термин «хеширование».

Идеология

Как обычно (математик я, что уж тут поделать) сформулируем аксиомы, которые вкладываются в предложение:

Все передаваемые файлы делятся на главные (в основном html-страницы) и подчинённые (скрипты, изображения, стили и т.д.).
В идеологии, заложенной в стандарты HTTP-кэширования, все файлы равноправны

Это, конечно, толерантно, но не отвечает современным реалиям.

Неважно, откуда получен подчинённый файл. Важно, что его содержимое удовлетворяет нужды главного.
В существующей идеологии даже сама аббревиатура URI — Uniform Resource Identifier — предполагает, что идентификатором ресурса является его адрес в сети

Но, увы, для подчинённых файлов это несколько не соответствует действительности.

Где и как используют хеширование

Например, простые хэш-функции (не надежные, но быстро рассчитываемые) применяются при проверке целостности передачи пакетов по протоколу TCP/IP (и ряду других протоколов и алгоритмов, для выявления аппаратных ошибок и сбоев — так называемое избыточное кодирование). Если рассчитанное значение хеша совпадает с отправленным вместе с пакетом (так называемой контрольной суммой), то значит потерь по пути не было (можно переходить к следующему пакету).

А это, ведь на минутку, основной протокол передачи данных в сети интернет. Без него никуда. Да, есть вероятность, что произойдет накладка — их называют коллизиями. Ведь для разных изначальных данных может получиться один и тот же хеш. Чем проще используется функция, тем выше такая вероятность. Но тут нужно просто выбирать между тем, что важнее в данный момент — надежность идентификации или скорость работы. В случае TCP/IP важна именно скорость. Но есть и другие области, где важнее именно надежность.

Похожая схема используется и в технологии блокчейн, где хеш выступает гарантией целостности цепочки транзакций (платежей) и защищает ее от несанкционированных изменений. Благодаря ему и распределенным вычислениям взломать блокчен очень сложно и на его основе благополучно существует множество криптовалют, включая самую популярную из них — это биткоин. Последний существует уже с 2009 год и до сих пор не был взломан.

Более сложные хеш-функции используются в криптографии. Главное условие для них — невозможность по конечному результату (хэшу) вычислить начальный (массив данных, который обработали данной хеш-функцией). Второе главное условие — стойкость к коллизиями, т.е. низкая вероятность получения двух одинаковых хеш-сумм из двух разных массивов данных при обработке их этой функцией. Расчеты по таким алгоритмам более сложные, но тут уже главное не скорость, а надежность.

Так же хеширование используется в технологии электронной цифровой подписи. С помощью хэша тут опять же удостоверяются, что подписывают именно тот документ, что требуется. Именно он (хеш) передается в токен, который и формирует электронную цифровую подпись. Но об этом, я надеюсь, еще будет отдельная статья, ибо тема интересная, но в двух абзацах ее не раскроешь.

Для доступа к сайтам и серверам по логину и паролю тоже часто используют хеширование. Согласитесь, что хранить пароли в открытом виде (для их сверки с вводимыми пользователями) довольно ненадежно (могут их похитить). Поэтому хранят хеши всех паролей. Пользователь вводит символы своего пароля, мгновенно рассчитывается его хеш-сумма и сверяется с тем, что есть в базе. Надежно и очень просто. Обычно для такого типа хеширования используют сложные функции с очень высокой криптостойкостью, чтобы по хэшу нельзя было бы восстановить пароль.

Какими свойствами должна обладать хеш-функция

Хочу систематизировать кое-что из уже сказанного и добавить новое.

1. Как уже было сказано, функция эта должна уметь приводить любой объем данных (а все они цифровые, т.е. двоичные, как вы понимаете) к числу заданной длины (по сути это сжатие до битовой последовательности заданной длины хитрым способом).
2. При этом малейшее изменение (хоть на один бит) входных данных должно приводить к полному изменению хеша.
3. Она должна быть стойкой в обратной операции, т.е. вероятность восстановления исходных данных по хешу должна быть весьма низкой (хотя последнее сильно зависит от задействованных мощностей)
4. В идеале она должна иметь как можно более низкую вероятность возникновения коллизий. Согласитесь, что не айс будет, если из разных массивов данных будут часто получаться одни и те же значения хэша.
5. Хорошая хеш-функция не должна сильно нагружать железо при своем исполнении. От этого сильно зависит скорость работы системы на ней построенной. Как я уже говорил выше, всегда имеется компромисс между скорость работы и качеством получаемого результата.
6. Алгоритм работы функции должен быть открытым, чтобы любой желающий мог бы оценить ее криптостойкость, т.е. вероятность восстановления начальных данных по выдаваемому хешу.

Проблемы хэшей

Одна из проблем криптографических функций хеширования — неизбежность коллизий. Раз речь идет о строке фиксированной длины, значит, существует вероятность, что для каждого ввода возможно наличие и других входов, способных привести к тому же самому хешу. В результате хакер может создать коллизию, позволяющую передать вредоносные данные под видом правильного хэша.

Цель хороших криптографических функций — максимально усложнить вероятность нахождения способов генерации входных данных, хешируемых с одинаковым значением. Как уже было сказано ранее, вычисление хэша не должно быть простым, а сам алгоритм должен быть устойчив к «атакам нахождения прообраза». Необходимо, чтобы на практике было чрезвычайно сложно (а лучше — невозможно) вычислить обратные детерминированные шаги, которые предприняты для воспроизведения созданного хешем значения.

Если S = hash (x), то, в идеале, нахождение x должно быть практически невозможным.

Хеш — это маркер целостности скачанных в сети файлов

Где еще можно встретить применение этой технологии? Наверняка при скачивании файлов из интернета вы сталкивались с тем, что там приводят некоторые числа (которые называют либо хешем, либо контрольными суммами) типа:

CRC32: 7438E546
MD5: DE3BAC46D80E77ADCE8E379F682332EB
SHA-1: 332B317FB97126B0F79F7AF5786EBC51E5CC82CF

Что это такое? И что вам с этим всем делать? Ну, как правило, на тех же сайтах можно найти пояснения по этому поводу, но я не буду вас утруждать и расскажу в двух словах. Это как раз и есть результаты работы различных хеш-функций (их названия приведены перед числами: CRC32, MD5 и SHA-1).

Зачем они вам нужны? Ну, если вам важно знать, что при скачивании все прошло нормально и ваша копия полностью соответствует оригиналу, то нужно будет поставить на свой компьютер программку, которая умеет вычислять хэш по этим алгоритмам (или хотя бы по некоторым их них). После чего прогнать скачанные файлы через эту программку и сравнить полученные числа с приведенными на сайте

Если совпадают, то сбоев при скачивании не было, а если нет, то значит были сбои и есть смысл повторить закачку заново

После чего прогнать скачанные файлы через эту программку и сравнить полученные числа с приведенными на сайте. Если совпадают, то сбоев при скачивании не было, а если нет, то значит были сбои и есть смысл повторить закачку заново.

Популярные хэш-алгоритмы сжатия

1. CRC32 — используется именно для создания контрольных сумм (так называемое избыточное кодирование). Данная функция не является криптографической. Есть много вариаций этого алгоритма (число после CRC означает длину получаемого хеша в битах), в зависимости от нужной длины получаемого хеша. Функция очень простая и нересурсоемкая. В связи с этим используется для проверки целостности пакетов в различных протоколах передачи данных.
2. MD5 — старая, но до сих пор очень популярная версия уже криптографического алгоритма, которая создает хеш длиной в 128 бит. Хотя стойкость этой версии на сегодняшний день и не очень высока, она все равно часто используется как еще один вариант контрольной суммы, например, при скачивании файлов из сети.
3. SHA-1 — криптографическая функция формирующая хеш-суммы длиной в 160 байт. Сейчас идет активная миграция в сторону SHA-2, которая обладает более высокой устойчивостью, но SHA-1 по-прежнему активно используется хотя бы в качестве контрольных сумм. Но она так же по-прежнему используется и для хранения хешей паролей в базе данных сайта (об этом читайте выше).
4. ГОСТ Р 34.11-2012 — текущий российский криптографический (стойкий к взлому) алгоритм введенный в работу в 2013 году (ранее использовался ГОСТ Р 34.11-94). Длина выходного хеша может быть 256 или 512 бит. Обладает высокой криптостойкостью и довольно хорошей скоростью работы. Используется для электронных цифровых подписей в системе государственного и другого документооборота.

HashTab — вычисление хеша для любых файлов на компьютере

Она бесплатна для личного некоммерческого использования и покрывает с лихвой все, что вам может понадобиться от подобного рода софта. После ее скачивания и установки запускать ничего не надо. Просто кликаете правой кнопкой мыши по нужному файлу в Проводнике (или ТоталКомандере) и выбираете самый нижний пункт выпадающего меню «Свойства»:

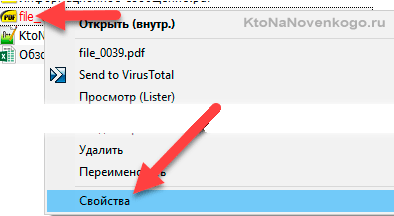
В открывшемся окне перейдите на вкладку «Хеш-суммы файлов», где будут отображены контрольные суммы, рассчитанные по нужным вам алгоритмам хэширования (задать их можно нажав на кнопку «Настройки» в этом же окне). По умолчанию отображаются три самых популярных:

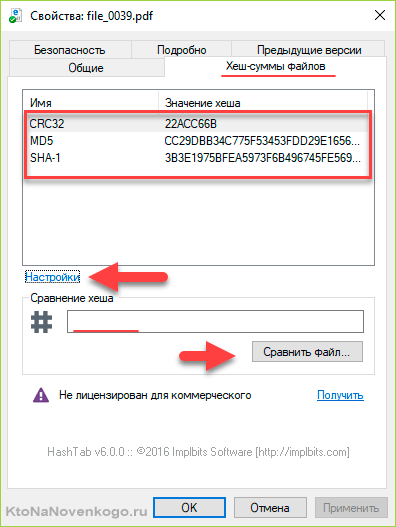
Чтобы не сравнивать контрольные суммы визуально, можно числа по очереди вставить в рассположенное ниже поле (со знаком решетки) и нажать на кнопку «Сравнить файл».

Как видите, все очень просто и быстро. А главное эффективно.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Применение хэш-функций

Хэш-функции широко используются в криптографии, а также во многих структурах данных — хеш-таблицах, фильтрах Блума и декартовых деревьях.

Криптографические хеш-функции

Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того, чтобы хеш-функция считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:

• Необратимость: для заданного значения хэш-функции m должно быть вычислительно невозможно найти блок данных, для которого.
• Устойчивость коллизиям первого рода: для заданного сообщения M должно быть вычислительно невозможно подобрать другое сообщение N, для которого.
• Устойчивость к коллизиям второго рода: должно быть вычислительно невозможно подобрать пару сообщений, имеющих одинаковый хеш.

Данные требования зависят друг от друга:

• Оборотная функция неустойчива к коллизиям первого и второго рода.
• Функция, неустойчивая к коллизиям первого рода, неустойчивая к коллизиям второго рода; обратное неверно.

Следует отметить, что не доказано существование необратимых хеш-функций, для которых вычисления любого прообраза заданного значения хэш-функции теоретически невозможно. Обычно нахождения обратного значения являются только вычислительно сложной задачей.

Атака «дней рождения» позволяет находить коллизии для хэш-функции с длиной значений n бит в среднем за примерно вычислений хэш-функции. Поэтому n — битная хэш-функция считается крипостийкою, если вычислительная сложность нахождения коллизий для нее близка к.

Для криптографических хэш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект). В частности, значение хеша не должно давать утечки информации, даже об отдельных биты аргумента

Это требование является залогом криптостойкости алгоритмов хеширования, хешуючих пароль пользователя для получения ключа.

Хеширования часто используется в алгоритмах электронно-цифровой подписи, где шифруется не самое сообщение, а его хэш, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев, вместо паролей хранятся значения их хеш-кодов.

Геометрическое хеширования

Геометрическое хеширования (англ. Geometric hashing) — широко применяемый в компьютерной графике и вычислительной геометрии метод для решения задач на плоскости или в трехмерном пространстве, например, для нахождения ближайших пар в множестве точек или для поиска одинаковых изображений. Хэш-функция в данном методе обычно получает на вход какой метрический пространство и разделяет его, создавая сетку из клеток. Таблица в данном случае является массивом с двумя или более индексами и называется файл сетки (англ. Grid file). Геометрическое хеширования также применяется в телекоммуникациях при работе с многомерными сигналами.

Ускорение поиска данных

Хеш-таблица — это структура данных, позволяет хранить пары вида (ключ, хеш-код) и поддерживает операции поиска, вставки и удаления элементов. Задачей хеш-таблиц является ускорение поиска, например, в случае записей в текстовых полей в базе данных может рассчитываться их хэш код и данные могут помещаться в раздел, соответствующий этому хэш-кода. Тогда при поиске данных надо будет сначала вычислить хэш текста и сразу станет известно, в каком разделе их надо искать, то есть, искать надо будет не по всей базе, а только по одному ее раздела (это сильно ускоряет поиск).

Бытовым аналогом хеширования в данном случае может служить размещение слов в словаре по алфавиту. Первая буква слова является его хеш-кодом, и при поиске мы просматриваем не весь словарь, а только нужную букву.

Реальный пример хеширования паролей Python

В следующем примере пароли будут хешироваться для последующего сохранения в базе данных. Здесь мы будем использовать . является случайной последовательностью, добавленной к строке пароля перед использованием хеш-функции. используется для предотвращения перебора по словарю (dictionary attack) и атак радужной таблицы (rainbow tables attacks).

Тем не менее, если вы занимаетесь реально функционирующим приложением и работаете над паролями пользователей, следите за последними зафиксированными уязвимостями в данной области. Для более подробного ознакомления с темой защиты паролей можете просмотреть следующую статью.

Код для Python 3.x

Python

import uuid
import hashlib

def hash_password(password):
# uuid используется для генерации случайного числа
salt = uuid.uuid4().hex
return hashlib.sha256(salt.encode() + password.encode()).hexdigest() + ‘:’ + salt

def check_password(hashed_password, user_password):
password, salt = hashed_password.split(‘:’)
return password == hashlib.sha256(salt.encode() + user_password.encode()).hexdigest()

new_pass = input(‘Введите пароль: ‘)
hashed_password = hash_password(new_pass)
print(‘Строка для хранения в базе данных: ‘ + hashed_password)
old_pass = input(‘Введите пароль еще раз для проверки: ‘)

if check_password(hashed_password, old_pass):
print(‘Вы ввели правильный пароль’)
else:
print(‘Извините, но пароли не совпадают’)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

importuuid importhashlib defhash_password(password) # uuid используется для генерации случайного числа salt=uuid.uuid4().hex returnhashlib.sha256(salt.encode()+password.encode()).hexdigest()+’:’+salt defcheck_password(hashed_password,user_password) password,salt=hashed_password.split(‘:’) returnpassword==hashlib.sha256(salt.encode()+user_password.encode()).hexdigest() new_pass=input(‘Введите пароль: ‘) hashed_password=hash_password(new_pass) print(‘Строка для хранения в базе данных: ‘+hashed_password) old_pass=input(‘Введите пароль еще раз для проверки: ‘) ifcheck_password(hashed_password,old_pass) print(‘Вы ввели правильный пароль’) else print(‘Извините, но пароли не совпадают’)

Код для Python 2.x

Python

import uuid
import hashlib

def hash_password(password):
# uuid используется для генерации случайного числа
salt = uuid.uuid4().hex
return hashlib.sha256(salt.encode() + password.encode()).hexdigest() + ‘:’ + salt

def check_password(hashed_password, user_password):
password, salt = hashed_password.split(‘:’)
return password == hashlib.sha256(salt.encode() + user_password.encode()).hexdigest()

new_pass = raw_input(‘Введите пароль: ‘)
hashed_password = hash_password(new_pass)
print(‘Строка для сохранения в базе данных: ‘ + hashed_password)
old_pass = raw_input(‘Введите пароль еще раз для проверки: ‘)
if check_password(hashed_password, old_pass):
print(‘Вы ввели правильный пароль’)
else:
print(‘Извините, но пароли не совпадают’)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

importuuid importhashlib defhash_password(password) # uuid используется для генерации случайного числа salt=uuid.uuid4().hex returnhashlib.sha256(salt.encode()+password.encode()).hexdigest()+’:’+salt defcheck_password(hashed_password,user_password) password,salt=hashed_password.split(‘:’) returnpassword==hashlib.sha256(salt.encode()+user_password.encode()).hexdigest() new_pass=raw_input(‘Введите пароль: ‘) hashed_password=hash_password(new_pass) print(‘Строка для сохранения в базе данных: ‘+hashed_password) old_pass=raw_input(‘Введите пароль еще раз для проверки: ‘) ifcheck_password(hashed_password,old_pass) print(‘Вы ввели правильный пароль’) else print(‘Извините, но пароли не совпадают’)

Почему нельзя хранить пароли в открытом виде

Главная причина — минимизация ущерба в случае утечки базы данных.

Но если в его руках окажутся логины и пароли, он может попытаться использовать эти данные для входа в почтовые сервисы (Gmail, Яндекс.Почта, Mail.ru и т.д.), социальные сети, мессенджеры, клиент-банки и т.д.

В тот же личный кабинет Пятёрочки, чтобы перевыпустить карту и потратить чужие бонусы.

В общем, пользователи сайта, которые везде используют одни и те же логины и пароли, могут получить кучу проблем.

Некоторые разработчики считают, что их приложение надёжно защищено и никаких утечек быть не может. Есть несколько причин, почему это мнение ошибочно:

• Разработчик — не робот, он не может не совершать ошибок.
• Взлом может произойти со стороны хостинг-провайдера, работу которого не всегда возможно контролировать.
• Некорректная настройка сервера может привести к возможному доступу других пользователей хостинга к вашему сайту (актуально для виртуальных хостингов).
• Бывший коллега по работе может слить базу данных конкурентам. Может в качестве мести, а может просто ради денег.

Короче, пароли в открытом виде хранить нельзя.

Описание

В настоящее время практически ни одно приложение криптографии не обходится без использования хэширования.

Хэш-функции – это функции, предназначенные для «сжатия» произвольного сообщения или набора данных, записанных, как правило, в двоичном алфавите, в некоторую битовую комбинацию фиксированной длины, называемую сверткой. Хэш-функции имеют разнообразные применения при проведении статистических экспериментов, при тестировании логических устройств, при построении алгоритмов быстрого поиска и проверки целостности записей в базах данных. Основным требованием к хэш-функциям является равномерность распределения их значений при случайном выборе значений аргумента.

Криптографической хеш-функцией называется всякая хеш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований специфичных для криптографических приложений. В криптографии хэш-функции применяются для решения следующих задач:

• построения систем контроля целостности данных при их передаче или хранении,
• аутентификация источника данных.

Хэш-функцией называется всякая функция h:X -> Y, легко вычислимая и такая, что для любого сообщения M значение h(M) = H (свертка) имеет фиксированную битовую длину. X — множество всех сообщений, Y — множество двоичных векторов фиксированной длины.
Как правило хэш-функции строят на основе так называемых одношаговых сжимающих функций y = f(x1, x2) двух переменных, где x1, x2 и y — двоичные векторы длины m, n и n соответственно, причем n — длина свертки, а m — длина блока сообщения.

Для получения значения h(M) сообщение сначала разбивается на блоки длины m (при этом, если длина сообщения не кратна m то последний блок неким специальным образом дополняется до полного), а затем к полученным блокам M1, M2,.., MN применяют следующую последовательную процедуру вычисления свертки:

Ho = v,
Hi = f(Mi,Hi-1), i = 1,.., N,
h(M) = HN
Здесь v — некоторая константа, часто ее называют инициализирующим вектором. Она выбирается
из различных соображений и может представлять собой секретную константу или набор случайных данных (выборку даты и времени, например).

При таком подходе свойства хэш-функции полностью определяются свойствами одношаговой сжимающей функции.

Выделяют два важных вида криптографических хэш-функций — ключевые и бесключевые. Ключевые хэш-функции называют кодами аутентификации сообщений. Они дают возможность без дополнительных средств гарантировать как правильность источника данных, так и целостность данных в системах с доверяющими друг другу пользователями.

Бесключевые хэш-функции называются кодами обнаружения ошибок. Они дают возможность с помощью дополнительных средств (шифрования, например) гарантировать целостность данных. Эти хэш-функции могут применяться в системах как с доверяющими, так и не доверяющими друг другу пользователями.

Последовательное хеширование с использованием трубы (|)

К примеру, нам нужно рассчитать sha256 хеш для строки ‘HackWare’; а затем для полученной строки (хеша), рассчитать хеш md5. Задача кажется очень тривиальной:

echo -n 'HackWare' | sha256sum | md5sum

Но это неправильный вариант. Поскольку результатом выполнения в любом случае является непонятная строка из случайных символов, трудно не только обнаружить ошибку, но даже понять, что она есть. А ошибок здесь сразу несколько! И каждая из них ведёт к получению абсолютно неправильных данных.

Даже очень бывалые пользователи командной строки Linux не сразу поймут в чём проблема, а обнаружив первую проблему не сразу поймут, что есть ещё одна.

Очень важно помнить, что в строке вместе с хешем всегда выводится имя файла, поэтому выполняя довольно очевидную команду вроде следующей:

echo -n 'HackWare' | sha256sum | md5sum

мы получим совсем не тот результат, который ожидаем. Мы предполагаем посчитать sha256 хеш строки ‘HackWare’, а затем для полученной строки (хеша) рассчитать новый хеш md5. На самом деле, md5sum рассчитывает хеш строки, к которой прибавлено « -». Т.е. получается совершенно другой результат.

Выше уже рассмотрено, как из вывода удалять « -», кажется, теперь всё должно быть в порядке:

echo -n 'HackWare' | sha256sum | awk '{print $1}' | md5sum

Давайте разобьём это действие на отдельные команды:

echo -n 'HackWare' | sha256sum | awk '{print $1}'

Получаем

353b717198496e369cff5fb17bc8be8a1d8e6e6e30be65d904cd000ebe394833

Второй этап хеширования:

echo -n '353b717198496e369cff5fb17bc8be8a1d8e6e6e30be65d904cd000ebe394833' | md5sum
0fcc41fc5d3d7b09e35866cd6e831085  -

Это и есть правильный ответ.

Попробуем выполнить

echo -n 'HackWare' | sha256sum | awk '{print $1}' | md5sum

Мы получим:

379f867937e7a241f7c7609f1d84d11f  —

Проблема в том, что когда выводится промежуточный хеш, к нему добавляется символ новой строки, и второй хеш считается по этой полной строке, включающей невидимый символ!

Используя printf можно вывести результат без конечного символа новой строки:

printf '%s' `echo -n 'HackWare' | sha256sum | awk '{print $1}'` | md5sum

Результат вновь правильный:

0fcc41fc5d3d7b09e35866cd6e831085  —

С printf не все дружат и проблематично использовать рассмотренную конструкцию если нужно хешировать более трёх раз, поэтому лучше использовать tr:

echo -n 'HackWare' | sha256sum | awk '{print $1}' | tr -d '\n' | md5sum

Вновь правильный результат:

0fcc41fc5d3d7b09e35866cd6e831085  —

Или даже сделаем ещё лучше – с программой awk будем использовать printf вместо print (это самый удобный и короткий вариант):

echo -n 'HackWare' | sha256sum | awk '{printf $1}' | md5sum

Алгоритм MD5 и его подверженность взлому

MD5 hash — один из первых стандартов алгоритма, который применялся в целях проверки целостности файлов (контрольных сумм). Также с его помощью хранили пароли в базах данных web-приложений. Функциональность относительно проста — алгоритм выводит для каждого ввода данных фиксированную 128-битную строку, задействуя для вычисления детерминированного результата однонаправленные тривиальные операции в нескольких раундах. Особенность — простота операций и короткая выходная длина, в результате чего MD5 является относительно легким для взлома. А еще он обладает низкой степенью защиты к атаке типа «дня рождения».

Атака дня рождения

Если поместить 23 человека в одну комнату, можно дать 50%-ную вероятность того, что у двух человек день рождения будет в один и тот же день. Если же количество людей довести до 70-ти, вероятность совпадения по дню рождения приблизится к 99,9 %. Есть и другая интерпретация: если голубям дать возможность сесть в коробки, при условии, что число коробок меньше числа голубей, окажется, что хотя бы в одной из коробок находится более одного голубя.

Вывод прост: если есть фиксированные ограничения на выход, значит, есть и фиксированная степень перестановок, на которых существует возможность обнаружить коллизию.

Когда разговор идет о сопротивлении коллизиям, то алгоритм MD5 действительно очень слаб. Настолько слаб, что даже бытовой Pentium 2,4 ГГц сможет вычислить искусственные хеш-коллизии, затратив на это чуть более нескольких секунд. Всё это в ранние годы стало причиной утечки большого количества предварительных MD5-прообразов.