Способы визуализации данных

Содержание:

КАСКАД ФАКТОРОВ
- Построение диаграммы «Каскад»
Анимированные диаграммы
Столбиковая диаграмма
Вы здесь
22.1.1 Простые столбчатые диаграммы
Круговая диаграмма
Столбиковая диаграмма
Что такое ярусная диаграмма?
Круговая столбчатая диаграмма
Анимированные диаграммы
Круговые диаграммы
Пример 1
История возникновения диаграмм
Линейная диаграмма (Line Charts)
Точечная диаграмма\Диаграмма рассеяния (Scatter Plot Chart)
Пример 1

КАСКАД ФАКТОРОВ

Рассмотрим еще одну проблему годового отчета. За отчетный год себестоимость выпускаемой продукции выросла с 1000 до 1730 тыс. руб. Это значительный рост затрат, который нужно объяснить руководству. Проводят факторный анализ.

Согласно факторному анализу себестоимость претерпевала значительные изменения под влиянием ряда факторов.

1. Факторы роста затрат:

увеличение фонда оплаты труда на 380 тыс. руб.;
рост цен на сырье и материалы добавил к затратам 240 тыс. руб.;
рост цен на энергоносители увеличил затраты компании на 300 тыс. руб.;
рост амортизационных отчислений составил 160 тыс. руб. Причины роста:

– в прошлом отчетном периоде ввели в эксплуатацию новую производственную линию № 5;

– завершили модернизацию оборудования и реконструкцию цеха № 2, что увеличило стоимость основных средств, а значит, и амортизационные отчисления;

на улучшение качества затратили 400 тыс. руб. Применили новые материалы, добавили дополнительные технологические операции, усилили контроль показателей качества. Это положительно повлияло на конкурентоспособность продукции.

2. Факторы снижения себестоимости:

снижение трудоемкости производственных операций позволило снизить себестоимость на 300 тыс. руб. Трудоемкость снижена в результате реализации мероприятий по внедрению бережливого производства в цехе № 1;
экономия материалов снизила себестоимость на 200 тыс. руб. Снизить расход материалов удалось благодаря запуску новой производственной линии № 5;
экономия по общепроизводственным расходам составила 250 тыс. руб. Экономию получили через оптимизацию численности инженерно-технического персонала цехов и общезаводских служб, автоматизацию рабочих мест мастеров, плановиков-диспетчеров, кладовщиков.

Все перечисленные факторы, которые отразились на отклонении фактической себестоимости от плановой, визуализированы на рис. 5.

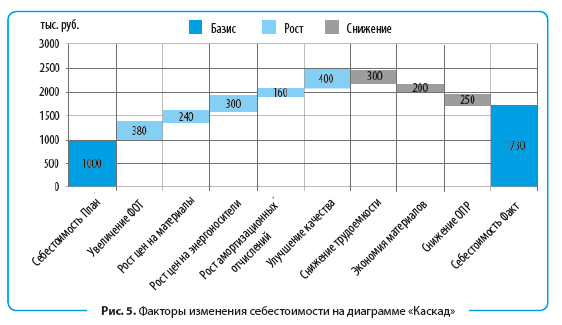
Построение диаграммы «Каскад»

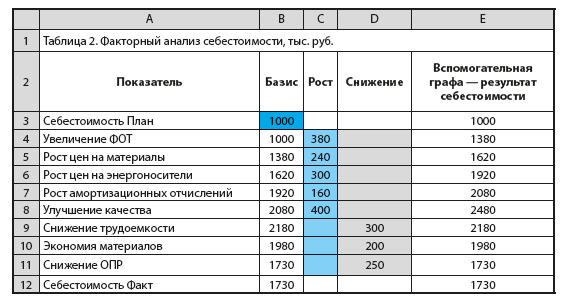
Чтобы построить «Каскад», важно правильно подготовить таблицу с диапазоном данных (табл. 2)

Диаграмму строят на основании граф «Показатель», «Базис», «Рост» и «Снижение».

В таблицу 2 вносят «Себестоимость План» и заполняют показатели в графах «Рост» и «Снижение». Во вспомогательной графе рассчитана фактическая себестоимость (видно, как она изменялась под влиянием каждого фактора). Показатели в графе «Базис» выполняют функцию «подпорок» (невидимая часть диаграммы).

Формула для графы «Базис»: =ЕСЛИ(C4>0;E4-C4+D4;E4).

Формула для вспомогательной графы: =E3+C4-D4.

После подготовки диапазона А3:D12 на вкладке Вставка выбирают Гистограмму с накоплением. Получают стандартную диаграмму, как на рис. 6. Для темно-зеленых столбиков гистограммы (базиса) вызывают контекстное меню: Формат ряда данных → Заливка → Нет заливки. Делают их невидимыми.

Отдельно для первого и последнего невидимого столбца («Себестоимость План» и «Себестоимость Факт») задают цвет: вкладка Формат → Заливка фигуры. Убирают легенду, добавляют подписи данных, форматируют шрифт и цвета видимых блоков гистограммы согласно корпоративным стандартам. В результате получают диаграмму «Каскад» с результатами факторного анализа, как на рис. 5.

Анимированные диаграммы

Виды связи в реляционной модели данных

В некоторых случаях стандартных свойств обычных неподвижных диаграмм и графиков бывает недостаточно. С целью повышения информативности, возникла идея: к обычным свойствам статичных диаграмм (формам, цветам, способам отображения и тематики) добавить свойство подвижности и изменения с течением времени. То есть представить диаграммы в виде определённых анимаций.

Группой исследователей из Массачусетского технологического института был найден способ отображения информации с помощью анимированных диаграмм. Разработанные ими диаграммы представляют собой анимированные интерактивные графики, работающие в режиме реального времени. В качестве примера разработки были взяты данные о поведении и действиях пользователей одного из сетевых ресурсов.

Под руководством Френсиса Лама (Francis Lam) исследователи создали два интерфейса анимированных диаграмм Seascape и Volcano. Характер изменений изображения на диаграммах свидетельствует о социальной активности пользователей ресурса. Например, размер квадратиков указывает на объём темы — чем больше площадь квадратика, тем больше объём обсуждаемой темы. Эти квадратики находятся в постоянном движении, представляющем собой, похожие на гармонические, колебания в плоскости диаграммы, смещающиеся линейно в какую-либо из сторон. По скорости движения можно судить об активности темы, а амплитуда колебаний показывает разницу во времени появления новых сообщений. В любой момент, наведя курсор в плоскость диаграммы, её можно остановить, выбрать интересующий квадратик и открыть тему, которой он соответствует. Открывающаяся в этом же окне тема, также представляет собой анимацию из кружочков, движущихся в разные стороны в пределах окна по типу Броуновского движения. Кружочки символизируют действия отдельных пользователей, и скорость их движения напрямую зависит от активности этих пользователей.

Seascape и Volcano отличаются друг от друга цветовой гаммой и количеством визуализированных данных. У Volcano, в отличие от Seascape отсутствуют волнообразные колебания.

По словам разработчиков, построение графиков с помощью анимированных диаграмм, должно позволить человеку быстрее воспринимать информацию с них путём привлечения внимания пользователя диаграммой и быстрой передачей данных в мозг. В данный момент ещё не приняты какие-либо требования или стандарты к генерации анимированных диаграмм.

Столбиковая диаграмма

Создание базы данных в excel по клиентам с примерами и шаблонами

На столбиковой диаграмме на линии абсцисс ( горизонтальной оси) отражаются интервалы времени, а на оси ординат ( вертикальной оси) — курс анализируемой акции. Верхняя точка диаграммы соответствует самому высокому курсу акции в этот день, а нижняя точка — самому низкому курсу. В какой-нибудь точке вертикальную линию пересекает небольшая горизонтальная линия, которая представляет цену закрытия акции на этот день.

Гистограммой называется столбиковая диаграмма ( см. рис. 19), которая строится на основе рядов частот следующим образом.

Если применяется столбиковая диаграмма, то вертикальное расположение столбцов более предпочтительно, чем горизонтальное, так как оно позволяет увидеть даже небольшое различие в высоте столбцов.

При выполнении столбиковой диаграммы координатную сетку не изображают, но базовую линию, от которой дают отсчет величины, выполняют обязательно. Столбики располагают на базовой линии.

При помощи столбиковой диаграммы изображают и структуру изучаемого явления. Диаграмма наглядно показывает повышение доли легковых автомашин в общем их производстве.

Графические элементы представлены столбиковыми диаграммами. Двузначная нумерация компонентов столбиковых диаграмм соответствует нумерации названий тематических направлений.

Одной из интересных вариаций современных столбиковых диаграмм является давнишний японский метод технического анализа, в котором используются диаграммы в виде свечей. Они довольно похожи на столбиковые диаграммы и, кроме прочих параметров, отражают еще и все уровни цены акции — начальную, высшую, низшую и цену закрытия, а не только три последних. Диаграмма, построенная таким образом, напоминает по виду свечку.

Профиль производственной мощности представляет собой столбиковую диаграмму, которую строят следующим образом. По оси абсцисс в произвольном масштабе откладывают равные отрезки, соответствующие цехам, отделениям или аппаратам в той последовательности, в которой они включены в линию потока. Отрезки служат основаниями столбиков, высота каждого из которых в определенном масштабе соответствует мощности определенного аппарата в пересчете либо на конечную продукцию, либо на сырье. Профиль производственной мощности дает наглядное представление о соответствии мощностей цехов, отделений, аппаратов.

Так как пиктограмма является разновидностью столбиковой диаграммы и ближайшей родственницей гистограммы, основной принцип — изображаемая величина представлена площадью фигуры — в полной мере сохраняется и по отношению к пиктограммам.

Предположим, что при создании столбиковой диаграммы для сравнения количеств заказов по месяцам вы хотите расположить столбцы в порядке возрастания количества заказов, а не в хронологическом порядке. Чтобы сделать это, вы должны объяснить Access, как расположить значения объемов продаж.

Все что было сказано о столбиковых диаграммах, полностью относится к полосовым диаграммам.

Столбиковая диаграмма имеет несколько разновидностей, например наслоенные и сложные столбиковые диаграммы, представленные на рис. 1.9 и 1.10, на которых отображены объемы производства четырех предприятий за три следующих друг за другом месяца.

На рис. 392 дан пример выполнения столбиковой диаграммы.

Гистограмма — это один из видов столбиковой диаграммы, дающей наглядное изображение того, с какой частотой повторяется то или иное значение или группа значений. Гистограмма показывает размах изменчивости процесса, помогает понять и проанализировать его динамику.

Все, что было сказано о столбиковых диаграммах, полностью относится к полосовым диаграммам. Различие только в том, что прямоугольники расположены горизонтально, а следовательно, базовая линия будет расположена вертикально.

Вы здесь

Тип данных

Главная › Математические программы › Самоучитель по SPSS › Глава 22. Стандартные графики

22.1.1 Простые столбчатые диаграммы

пт, 05/26/2006 — 07:45 — admin

22.1.1 Простые столбчатые диаграммы

Откройте файл с данными об исследовании гипертонии (файл hyper.sav).

Мы хотим построить столбчатую диаграмму для процентных показателей частот четырёх возрастных групп (переменная ak).

Щёлкните на области Simple (Простая) и оставьте предварительную установку Summaries for groups of cases (Обработка категорий одной переменной).
Щёлкните по кнопке Define (Определить); откроется соответствующее диалоговое окно.
В поле Category Axis: (Ось категорий) введите переменную ak, активируйте % of cases (% наблюдений) и, пройдя выключатель Titles… (Заголовок), введите заголовок для диаграммы.
Щёлкните на ОК.

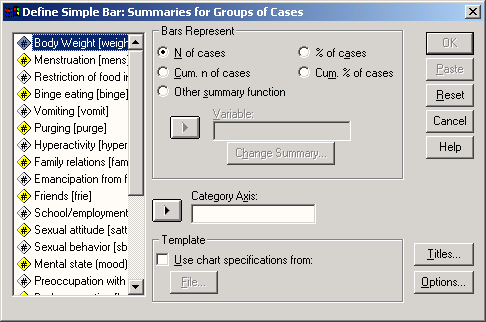
Рис. 22.3: Диалоговое окно Define Simple Bar: Summaries for groups of cases (Простая столбчатая диаграмма: Обработка категорий одной переменной)

Будет построен график, показанный на рисунке 22.4.

Теперь представим в графическом виде изменение среднего значения уровня сахара в крови (переменные bz0, bz1, bz6 и bz12), взятого из того же файла (hyper.sav).

В этот раз в диалоговом окне Ваг Charts (Столбчатые диаграммы) активируйте Summaries of separate variables (Обработка отдельных переменных); после нажатия выключателя Define (Определить) откроется соответствующее диалоговое окно (см. рис. 22.5).
В поле Bars Represent (Значения столбцов) по очереди внесите переменные bz0, bz1, bz6 и bz12 и оставьте установленную по умолчанию функцию Mean of values (Средние значения).
Пройдя выключатель Titles… (Заголовок), введите заголовок диаграммы.
Щёлкните на ОК.

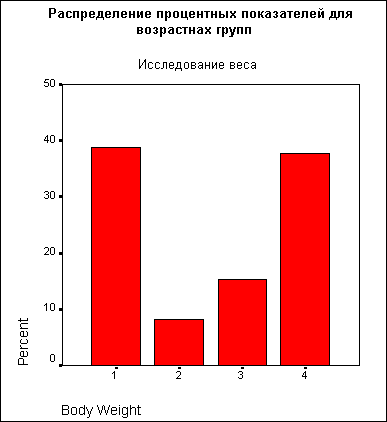
Рис. 22.4: Простая столбчатая диаграмма (Категории одной переменной)

Будет построен график, приведенный на рисунке 22.6.

Следует отметить тот недостаток, что в этой диаграмме не полностью приведены метки значений и на вертикальной оси показана только ограниченная область от 103,5 до 106,0, из-за чего по ошибке можно сделать неверное заключение о сильном изменении уровня сахара. Вы можете подкорректировать эти ошибки в редакторе диаграмм.

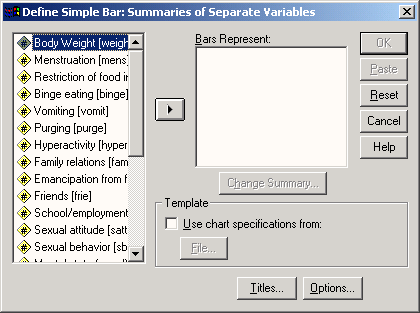
Рис. 22.5: Диалоговое окно Define Simple Bar: Summaries of separate variables (Построение простой столбчатой диаграммы: Обработка отдельных переменных)

Если Вы хотите выбрать функцию отличную от установленной по умолчанию Mean of values (Средние значения), щёлкните на одной из переменных в списке и затем на выключателе Change Summary…(Изменить метод обработки).

Откроется диалоговое окно с перечнем функций (см. рис. 22.7).

Это диалоговое окно появляется только для столбчатой, линейной, круговой диаграмм и диаграммы с областями, причём не каждая из находящихся здесь функций пригодна для всех видов диаграмм. Если для имеющихся данных Вы хотите отобразить медианы или другие процентили (сравните с гл. 6), то активируйте опцию Values are grouped midpoints (Значения являются сгруппированными средними точками).

В следующем примере рассматривается вопрос отображения готовых данных. Допустим, Вы взяли из некоторой газеты данные по 1993 году о добыче нефти в семи странах, входящих в ОРЕС и являющихся ведущими в этой отрасли.

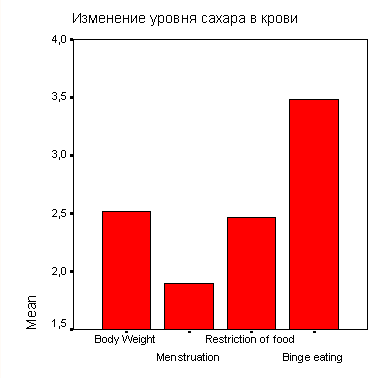
Рис. 22.6: Простая столбчатая диаграмма (Отдельные переменные)

Страна	Млн.баррель/день
Саудовская- Аравия	8,0
Иран	3,3
Венесуэла	2,3
Объединённые Арабские Эмираты	2,2
Нигерия	1,8
Кувейт	1,6
Ливия	1,4

Представим эти данные в форме столбчатой диаграммы.

Откройте файл oel.sav.
В диалоговом окне Bar Charts (Столбчатые диаграммы) активируйте опцию Values of individual cases (Значения отдельных наблюдений).

После нажатия выключателя Define (Определить) откроется соответствующее диалоговое окно.

В поле Bars Represent (Значения столбцов) внесите переменную barrel; в группе Category Labels (Метки категорий) активируйте Variable: (Переменная) и внесите переменную land.

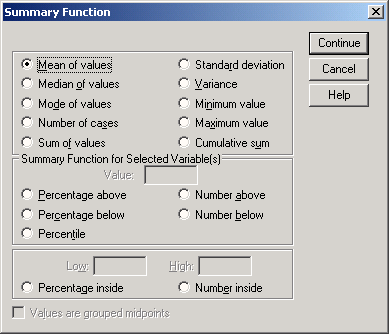
Рис. 22.7: Диалоговое окно Summary Function (Обрабатывающая функция).

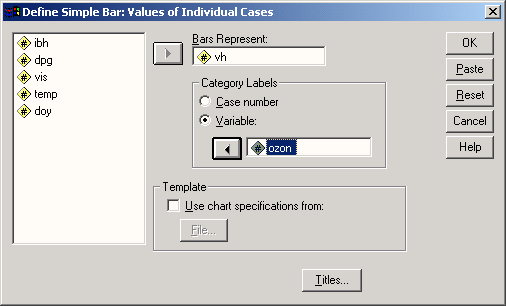
Рис. 22.8: Диалоговое окно Define Simple Bar: Values of individual cases (Построение простой столбчатой диаграммы: Значения отдельных случаев)

Пройдя выключатель Titles… (Заголовок), введите заголовок диаграммы и щёлкните на ОК.

График будет выглядеть так, как на рисунке 22.9.

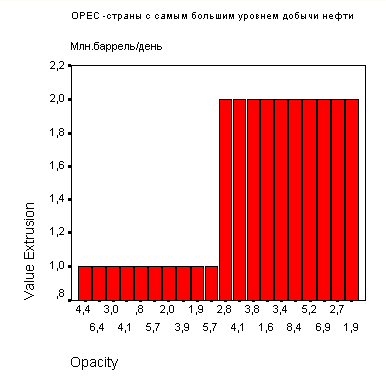
Рис. 22.9: Простая столбчатая диаграмма (Значения отдельных случаев)

Круговая диаграмма

Рис. 1. Круговая диаграмма площадей океанов от общей площади океанов

На рисунке 1 мы видим, что Тихий океан не только самый большой, но и занимает почти точную половину всего мирового океана.

Рассмотрим другой пример.

Четыре ближайшие планеты к Солнцу называются планетами земной группы.

Выпишем расстояние от Солнца до каждой из них.

До Меркурия 58 млн км

До Венеры 108 млн км

До Земли 150 млн км

До Марса 228 млн км

Мы опять можем построить круговую диаграмму. Она будет показывать, какой вклад расстояние для каждой планеты имеет в сумме всех расстояний. Но сумма всех расстояний не имеет для нас смысла. Полный круг не соответствует никакой величине (см. Рис. 2).

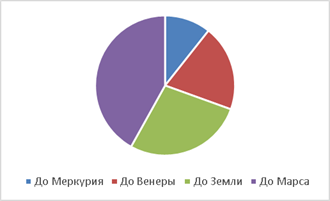
Рис. 2 Круговая диаграмма расстояний до Солнца

Так как сумма всех величин не имеет для нас смысла, то и нет смысла строить круговую диаграмму.

Столбиковая диаграмма

Столбиковая диаграмма используется чаще всего для сравнения одноименных показателей, характеризующих различные объекты или территории. Значения сравниваемых показателей изображаются при этом в виде прямоугольных столбиков, имеющих одинаковую ширину и расположенных на общей горизонтальной или вертикальной базовой линии. Высота ( или длина) каждого столбика в определенном масштабе соответствует величине изображаемого показателя. Столбики могут располагаться вплотную либо на одинаковом расстоянии друг от друга.

Столбиковая диаграмма, в которой расположение прямоугольников ( столбиков) показывает относительные величины выражаемого явления или процесса. Расположение прямоугольников может быть горизонтальным, один под одним, начиная с некоторой общей линии, или вертикальным, рядом друг с другом. В последнем случае все прямоугольники стоят на общей горизонтали.

Столбиковые диаграммы имеют удивительно четкую геометрическую форму. Поэтому многие специалисты технического анализа часто выражают общие тенденции движения прямыми линиями, устанавливающими границы колебаний. Это позволяет определить будущие точки поддержки и сопротивления.

Столбиковые диаграммы — показывают количественные изменения за определенный промежуток времени.

Гистограмма доходов.| Гистограмма показателей невыхода на работу.

Столбиковые диаграммы часто используются для отображения данных, относящихся к нечисловым, или качественным, переменным. Например, на рис. 1.7 представлена столбиковая диаграмма, отображающая дневную выработку четырех производственных предприятий. Цифры приведены в тыс. долл.

Столбиковая диаграмма — это один из немногих видов графиков, которые можно располагать как горизонтально, так и вертикально. На рис. 1.8 представлено стоимостное выражение экспорта ряда стран за определенный месяц. Цифры приведены в 10 млн. долл.

Столбиковые диаграммы являются наиболее простым видом диаграмм и применяются для изображения динамики или, структуры.

Фармацевтическая компания Хартвудз. объем продаж.

Данные статистического учета ОАО СибирЬко-Уральская алюминиевая компания. Полосовая диаграмма.

Разновидностью столбиковой диаграммы является полосовая ( ленточная) диаграмма, для которой характерны горизонтальная ориентация столбиков ( полос) и вертикальное расположение базовой линии.

Разновидностью столбиковых диаграмм являются ленточные диаграммы. Они изображают размеры признака в виде расположенных по горизонтали прямоугольников одинаковой ширины, но различной длины пропорционально изображаемым величинам. Начало полос должно находиться.

Что такое ярусная диаграмма?

Перед тем как мы приступим практике, давайте разберемся, что же такое ярусная диаграмма и с чем ее «едят»? Если взглянуть на прикрепленную ниже картинку, то мы увидим, что каждый столбик, отождествляющий в данном случае того или иного человека, состоит из нескольких частей. Так вот, каждая из таких частей и является ярусом.

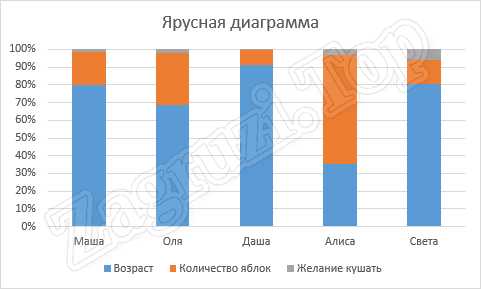
Проще говоря, для того чтобы отобразить несколько величин и при этом наглядно показать пропорции между ними в одном столбике, используется тип графика, показанного на прикрепленном выше скриншоте. Он же в простонародье и называется ярусной диаграммой. Дальше давайте разбираться, как построить такой индикатор в Microsoft Excel.

Круговая столбчатая диаграмма

Кольцевая, круговоая, или радиальная столбчатая диаграмма (radial column/bar chart) является вариацией на тему классической столбчатой диаграммы (bar chart).
Окружность в качестве оси абсцисс (X) и концентрические окружности в роли координатной решетки, вот собственно отличительные особенности это вида графика от обычной столбчатой диаграммы. Выглядит это всё следующим образом.

Тут есть один нюанс, а именно какую шкалу (scale) использовать? Дело в том, что чем дальше от центра, тем больше будет длина внешней дуги (C = 2πR) и площадь нашего сектора (S ~ πR2). Поэтому нам нужно решить что для нас важнее: компенсировать различный визуальный вес наших столбцов или сохранить регулярность сетки.

Для первого варианта можно использовать масштаб, предложенный Майком Бостоком:

Для регулярной сетки используйте стандартный линейный масштаб (). Я в своих примерах использовал именно его.

Анимированные диаграммы

Круговые диаграммы

Классическая круговая диаграмма

Круговые диаграммы – это наглядный способ показать доли компонент в наборе. Они идеально подходят для отчетов, презентаций и т.п. Для построения круговых диаграмм в Matplotlib используется функция pie().

Пример построения диаграммы:

vals = 
labels = 

fig, ax = plt.subplots()
ax.pie(vals, labels=labels)
ax.axis("equal")

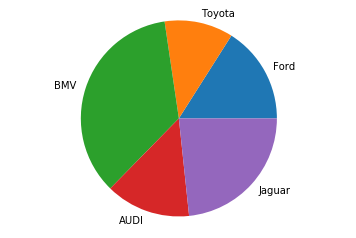
Рассмотрим параметры функции pie()

x: массив

Массив с размерами долей.
explode: массив, optional, значение по умолчанию:None

Если параметр не равен None, то часть долей, который перечислены в передаваемом значении будут вынесены из диаграммы на заданное расстояние, пример диаграммы:

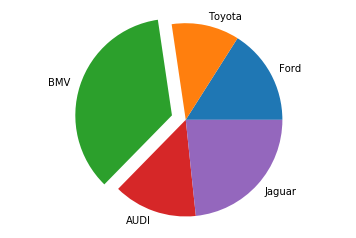
labels: list, optional, значение по умолчанию:None

Текстовые метки долей.
colors: массив, optional, значение по умолчанию: None

Цвета долей.
autopctstr, функция, optional, значение по умолчанию: None

Формат текстовой метки внутри доли, текст – это численное значение показателя, связанного с конкретной долей.
pctdistancefloat, optional, значение по умолчанию: 0.6

Расстояние между центром каждой доли и началом текстовой метки, которая определяется параметром autopct.
shadow: bool, optional, значение по умолчанию:False

Отображение тени для диаграммы.
labeldistancefloat, None, optional, значение по умолчанию: 1.1

Расстояние, на котором будут отображены текстовые метки долей. Если параметр равен None, то метки не будет отображены.
startangle: float, optional, значение по умолчанию:None

Задает угол, на который нужно повернуть диаграмму против часовой стрелке относительно оси x.
radius: float, optional, значение по умолчанию:None

Величина радиуса диаграммы.
counterclockbool, optional, значение по умолчанию:True

Определяет направление вращения – по часовой или против часовой стрелки.
wedgeprops: dict, optional, значение по умолчанию:None

Словарь параметров, определяющих внешний вид долей.
textprops: dict, optional, значение по умолчанию:None

Словарь параметров определяющих внешний вид текстовых меток.
centerlist значений float, optional, значение по умолчанию: (0, 0)

Центр диаграммы.
framebool, optional, значение по умолчанию:False

Если параметр равен True, то вокруг диаграммы будет отображена рамка.
rotatelabelsbool, optional, значение по умолчанию:False

Если параметр равен True, то текстовые метки будут повернуты на угол.

Создадим пример, в котором продемонстрируем работу с параметрами функции pie()

vals = 

labels = 

explode = (0.1, 0, 0.15, 0, 0)

fig, ax = plt.subplots()
ax.pie(vals, labels=labels, autopct='%1.1f%%', shadow=True, explode=explode, wedgeprops={'lw':1, 'ls':'--','edgecolor':"k"}, rotatelabels=True)
ax.axis("equal")

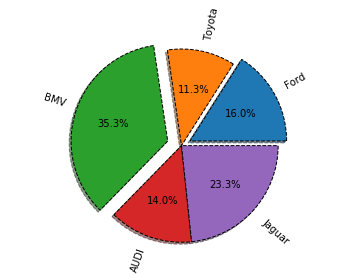
Вложенные круговые диаграммы

Рассмотрим пример построения вложенной круговой диаграммы. Такая диаграмма состоит из двух компонент: внутренняя ее часть является детальным представлением информации, а внешняя – суммарную по заданным областям. Каждая область представляет собой список численных значений, вместе они образуют общий набор данных. Рассмотрим на примере:

fig, ax = plt.subplots()

offset=0.4

data = np.array(, , ])
cmap = plt.get_cmap("tab20b")

b_colors = cmap(np.array())
sm_colors = cmap(np.array())

ax.pie(data.sum(axis=1), radius=1, colors=b_colors, wedgeprops=dict(width=offset, edgecolor='w'))
ax.pie(data.flatten(), radius=1-offset, colors=sm_colors, wedgeprops=dict(width=offset, edgecolor='w'))

Круговая диаграмма в виде бублика

Построим круговую диаграмму в виде бублика (с отверстием посередине). Это можно сделать через параметр wedgeprops, который отвечает за внешний вид долей:

vals = 
labels = 

fig, ax = plt.subplots()
ax.pie(vals, labels=labels, wedgeprops=dict(width=0.5))

Пример 1

Построить столбчатую диаграмму расстояний от Солнца до ближайших 4-х планет и ближайшей звезды.

Про планеты мы уже знаем, а ближайшая звезда – Проксима Центавра (см. Табл. 2).

До Меркурия	58
До Венеры	108
До Земли	150
До Марса	228
До Проксимы Центавра	40 000 000

Табл. 2

Все расстояния снова указаны в миллионах километров.

Строим столбчатую диаграмму (см. Рис. 6).

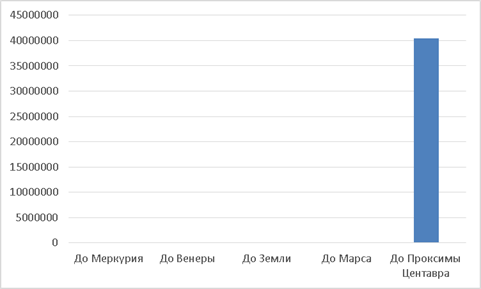
Рис. 6. Столбчатая диаграмма расстояния от солнца до планет земной группы и ближайшей звезды

Но расстояние до звезды так огромно, что на его фоне расстояния до четырех планет становятся неразличимы.

Диаграмма потеряла всякий смысл.

Вывод такой: нельзя строить диаграмму по данным, которые отличаются друг от друга в тысячи или более раз.

А что делать?

Нужно разбить данные на группы. Для планет построить одну диаграмму, как мы делали, для звезд – другую.

История возникновения диаграмм

График функции f(x)=x3 {\displaystyle f(x)={x^{3}}\!\ }

Во всех диаграммах используется функциональная зависимость как минимум двух типов данных. Соответственно, первыми диаграммами были обыкновенные графики функций, в которых допустимые значения аргумента соответствуют значениям функций.

Идеи функциональной зависимости использовались в древности. Она обнаруживается уже в первых математически выраженных соотношениях между величинами, а также в первых правилах действий над числами, в первых формулах для нахождения площади и объёма геометрических фигур. Вавилонские учёные, таким образом, несознательно установили, что площадь круга является функцией от его радиуса 4—5 тыс. лет назад. Астрономические таблицы вавилонян, древних греков и индийцев — яркий пример табличного задания функции, а таблицы, соответственно, являются хранилищем данных для диаграмм.

В XVII веке французские учёные Франсуа Виет и Рене Декарт заложили основы понятия функции и разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Также геометрические работы Декарта и Пьера Ферма проявили отчётливое представление переменной величины и прямоугольной системы координат — вспомогательных элементов всех современных диаграмм.

Первые статистические графики начал строить английский экономист У. Плейфер в работе «Коммерческий и политический атлас» 1786 года. Это произведение послужило толчком для развития графических методов в общественных науках.

Линейная диаграмма (Line Charts)

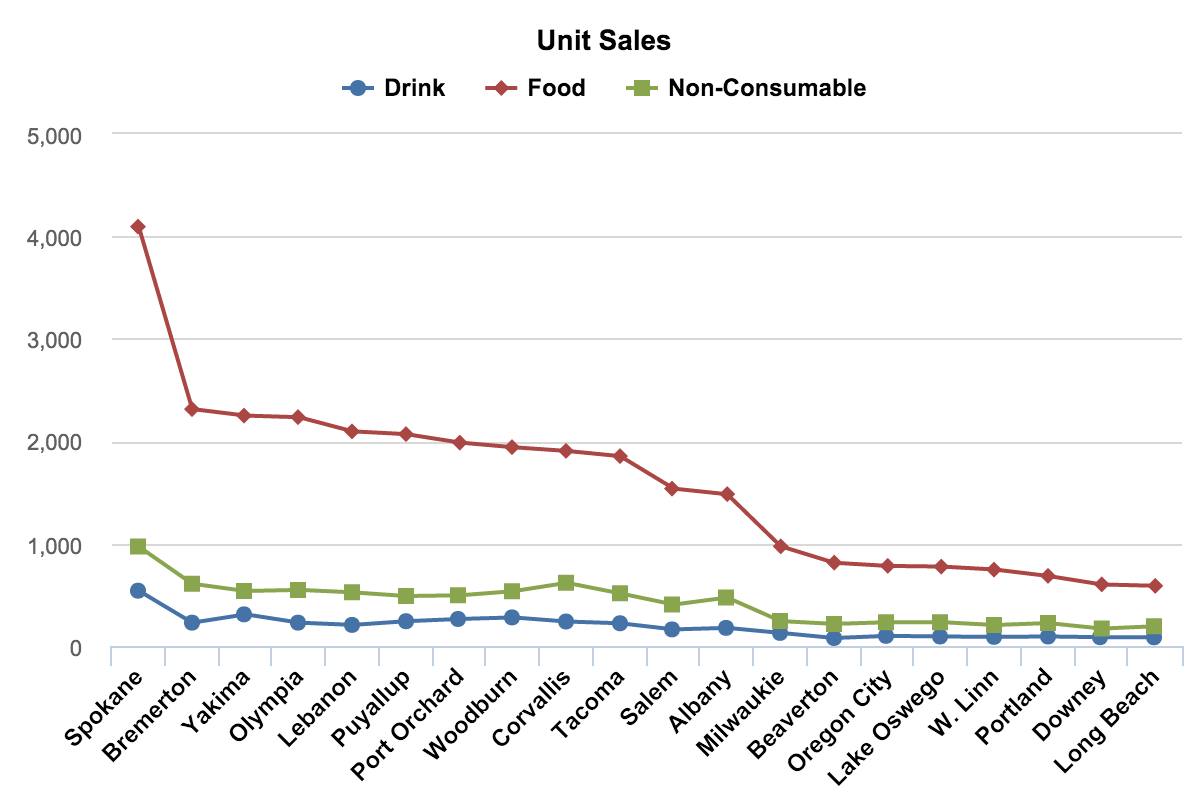
Впервые с линейной диаграммой мы знакомимся с в школе, когда чертим график функции в системе координат. Линейная диаграмма отлично подходит , если —

набор ваших данных непрерывен;
количество значений больше 20;
вы хотите показать тренд изменений значений.

В этом типе диаграмм возможность сравнивать значения уходит на второй план, но все еще остается возможной, с помощью маркеров на графике, которые ставятся через одинаковые промежутки.

Советы для линейной диаграммы

Линейные диаграммы хорошо подходят, чтобы показать непрерывные данные, разбитые на равные по размеру интервалы.
Начинайте ось значений всегда с нуля. Если у вас появилась крутая идея начать не с нуля, скорее всего вы не правы.
Время в линейной диаграмме всегда идет слева направо.
Не пропускайте значения в интервалах данных, если они равны нулю или выбиваются из общих значениях. Например, определенные дни с нулевыми значениями, если во все остальные дни значения не нулевые.
Если вам нужно подчеркнуть тренд, удалите все подписи к значениям диаграммы.
Для подписей интервалов на диаграмме используйте наклон в 45 градусов слева направо.

Точечная диаграмма\Диаграмма рассеяния (Scatter Plot Chart)

Диаграммы рассеяния в основном используются для анализа корреляции и распределения. Хорошо показывает связь между двумя разными переменными, где одна коррелирует с другой (или не коррелирует). Также могут показывать тенденции распространения данных или кластеризации и помогают выявлять аномалии или выбросы.

Хорошим примером диаграмм рассеяния будет диаграмма, показывающая расходы на маркетинг и доходы.