Сортировка слиянием с реализацией на python

Функции из модуля operator

Шаблон с ключевой функций, показанный выше, используется очень часто, поэтому Python предоставляет функции для быстрого создания функций доступа. Модуль operator содержит функции: itemgetter(), attrgetter(), и methodcaller().

Используя эти функции, примеры выше становятся проще и быстрее:

>>> from operator import itemgetter, attrgetter

1	>>>from operator import itemgetter,attrgetter

>>> sorted(student_tuples, key=itemgetter(2))

1 2	>>>sorted(student_tuples,key=itemgetter(2)) (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

>>> sorted(student_objects, key=attrgetter(‘age’))

1 2	>>>sorted(student_objects,key=attrgetter(‘age’)) (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Функции модуля operator позволяют несколько уровней сортировки. Для примера, сортировка по классу и по возрасту:

>>> sorted(student_tuples, key=itemgetter(1,2))

1 2	>>>sorted(student_tuples,key=itemgetter(1,2)) (‘john’,’A’,15),(‘dave’,’B’,10),(‘jane’,’B’,12)

>>> sorted(student_objects, key=attrgetter(‘grade’, ‘age’))

1 2	>>>sorted(student_objects,key=attrgetter(‘grade’,’age’)) (‘john’,’A’,15),(‘dave’,’B’,10),(‘jane’,’B’,12)

Старый способ использования параметра cmp

Многие конструкции, приведенные в этом HOWTO, предполагают Python 2.4 или новее. До этого не было встроенных функций и c аргументами ключевых слов. Вместо этого все версии Py2.x поддерживали параметр для обработки заданных пользователем функций сравнения.

В Py3.0 параметр был полностью удален (как часть более масштабных усилий по упрощению и унификации языка, устраняя конфликт между богатыми сравнениями и магическим методом .

В Py2.x сортировка допускает необязательную функцию, которая может быть вызвана для сравнения. Эта функция должна принимать два аргумента для сравнения, а затем возвращать отрицательное значение для «меньше», возвращать ноль, если они равны, или возвращать положительное значение для «больше». Например, мы можем:

>>> def numeric_compare(x, y):
...    return x - y

>>> sorted(, cmp=numeric_compare) 

Или вы можете изменить порядок сравнения:

>>> def reverse_numeric(x, y):
...    return y - x

>>> sorted(, cmp=reverse_numeric) 

При переносе кода с Python 2.x на 3.x может возникнуть ситуация, когда у вас есть пользователь, предоставляющий функцию сравнения, и вам нужно преобразовать ее в ключевую функцию. Следующая оболочка упрощает это:

def cmp_to_key(mycmp):
    'Convert a cmp= function into a key= function'
    class K:
        def __init__(self, obj, *args):
            self.obj = obj
        def __lt__(self, other):
            return mycmp(self.obj, other.obj)  0
        def __eq__(self, other):
            return mycmp(self.obj, other.obj) == 0
        def __le__(self, other):
            return mycmp(self.obj, other.obj) = 0
        def __ne__(self, other):
            return mycmp(self.obj, other.obj) != 0
    return K

Чтобы преобразовать в ключевую функцию, просто оберните старую функцию сравнения:

>>> sorted(, key=cmp_to_key(reverse_numeric))

В Python 3.2 функция была добавлена ​​в модуль в стандартной библиотеке.

Адаптация алгоритма для сортировки

• Вся возня с буфером обмена и его последующее слияние с массивом нужны только если в массиве в самом деле не было свободного места. Если мы сливаем фрагменты длиной A и B, а после них есть еще хотя бы S ячеек неотсортированного пространства, то нам достаточно разбить массивы на куски, отсортировать их и слить. Особенно эффективно это будет работать, если S=A=B.
• Надо постараться, чтобы длина остатка была нулевой, а граница между отсортированными фрагментами попала точно на границу кусков длины S. Проще всего этого добиться, если выбрать S равным степени двойки, а A и B заставить делиться на него.
• Сортировка кусков массивов требует ((A+B)/S)2/2 сравнений. Последующая сортировка буфера обмена – O(S*log( S )) сравнений. Поэтому выбирать S близким к sqrt(N) не обязательно, можно увеличить его, например, до N/log(N).

алгоритм примерно в сотню строк8выигрываетRRRUPD:

Сортировка включением

Одним из наиболее простых и естественных методов внутренней сортировки является сортировка простыми включениями. Идея алгоритма очень проста. Пусть имеется массив ключей Arr, Arr₁, …, Arr_N‑1. Для каждого элемента массива, начиная со второго, производится сравнение с элементами с меньшим индексом. Элемент Arr_i последовательно сравнивается с элементами Arr_j, где jЄ, т.е. изменяется от i‑1 до 0. До тех пор, пока для очередного элемента Arr_j выполняется соотношение Arr_j > Arr_i, Arr_i и Arr_j меняются местами. Если удается встретить такой элемент Arr_j, что Arr_j ≤ Arr_i, или если достигнута нижняя граница массива, производится переход к обработке элемента Arr_i+1. Так продолжается до тех пор, пока не будет достигнута верхняя граница массива.

Легко видеть, что в лучшем случае, когда массив уже упорядочен для выполнения алгоритма с массивом из N элементов потребуется N‑1 сравнение и 0 пересылок. В худшем случае, когда массив упорядочен в обратном порядке потребуется N(N‑1)/2 сравнений и столько же пересылок. Таким образом, можно оценивать сложность метода простых включений как O(N2).

Можно сократить число сравнений, применяемых в методе простых включений, если воспользоваться тем, что при обработке элемента Arr_i массива элементы Arr, Arr₁, …, Arr_i‑1 уже упорядочены, и воспользоваться для поиска элемента, с которым должна быть произведена перестановка, методом двоичного деления. В этом случае оценка числа требуемых сравнений становится O(N*Log(N)). Заметим, что поскольку при выполнении перестановки требуется сдвижка на один элемент нескольких элементов, то оценка числа пересылок остается O(N2). Алгоритм сортировки включением, оформленный в виде функции приведен ниже.

Sort Stability and Complex Sorts¶

Sorts are guaranteed to be . That means that
when multiple records have the same key, their original order is preserved.

>>> data = 
>>> sorted(data, key=itemgetter())

Notice how the two records for blue retain their original order so that
is guaranteed to precede .

This wonderful property lets you build complex sorts in a series of sorting
steps. For example, to sort the student data by descending grade and then
ascending age, do the age sort first and then sort again using grade:

>>> s = sorted(student_objects, key=attrgetter('age'))     # sort on secondary key
>>> sorted(s, key=attrgetter('grade'), reverse=True)       # now sort on primary key, descending

This can be abstracted out into a wrapper function that can take a list and
tuples of field and order to sort them on multiple passes.

>>> def multisort(xs, specs):
...     for key, reverse in reversed(specs):
...         xs.sort(key=attrgetter(key), reverse=reverse)
...     return xs

>>> multisort(list(student_objects), (('grade', True), ('age', False)))

Простая сортировка

Чтобы отсортировать список по возрастанию вызовите функцию sorted(). Функция вернёт новый сортированный список:

>>>
>>> sorted()

1 2 3

>>> >>>sorted(5,2,3,1,4) 1,2,3,4,5

Метод сортирует список у которого вызван и возвращает None. Если исходный список больше не нужен это может быть немного эффективнее:

>>> a =
>>> a.sort()
>>> a

1 2 3 4

>>>a=5,2,3,1,4 >>>a.sort() >>>a 1,2,3,4,5

Метод определён только для списков. В отличи от него, функция sorted() работает с любыми перечисляемыми объектами:

>>> sorted({1: ‘D’, 2: ‘B’, 3: ‘B’, 4: ‘E’, 5: ‘A’})

1 2	>>>sorted({1’D’,2’B’,3’B’,4’E’,5’A’}) 1,2,3,4,5

The Old Way Using the cmp Parameter¶

Many constructs given in this HOWTO assume Python 2.4 or later. Before that,
there was no builtin and took no keyword
arguments. Instead, all of the Py2.x versions supported a cmp parameter to
handle user specified comparison functions.

In Py3.0, the cmp parameter was removed entirely (as part of a larger effort to
simplify and unify the language, eliminating the conflict between rich
comparisons and the magic method).

In Py2.x, sort allowed an optional function which can be called for doing the
comparisons. That function should take two arguments to be compared and then
return a negative value for less-than, return zero if they are equal, or return
a positive value for greater-than. For example, we can do:

>>> def numeric_compare(x, y):
...     return x - y
>>> sorted(, cmp=numeric_compare) 

Or you can reverse the order of comparison with:

>>> def reverse_numeric(x, y):
...     return y - x
>>> sorted(, cmp=reverse_numeric) 

When porting code from Python 2.x to 3.x, the situation can arise when you have
the user supplying a comparison function and you need to convert that to a key
function. The following wrapper makes that easy to do:

def cmp_to_key(mycmp):
    'Convert a cmp= function into a key= function'
    class K
        def __init__(self, obj, *args):
            self.obj = obj
        def __lt__(self, other):
            return mycmp(self.obj, other.obj) < 
        def __gt__(self, other):
            return mycmp(self.obj, other.obj) > 
        def __eq__(self, other):
            return mycmp(self.obj, other.obj) == 
        def __le__(self, other):
            return mycmp(self.obj, other.obj) <= 
        def __ge__(self, other):
            return mycmp(self.obj, other.obj) >= 
        def __ne__(self, other):
            return mycmp(self.obj, other.obj) != 
    return K

To convert to a key function, just wrap the old comparison function:

>>> sorted(, key=cmp_to_key(reverse_numeric))

Стабильность сортировки и сложные сортировки

Сортировки гарантированно . Это означает, что когда несколько записей имеют один и тот же ключ, их исходный порядок сохраняется.

>>> data = 
>>> sorted(data, key=itemgetter(0))

Обратите внимание, что две записи для сохраняют свой исходный порядок, поэтому гарантированно предшествует. Это замечательное свойство позволяет создавать сложные сортировки в несколько этапов

Например, чтобы отсортировать данные учащиеся по убыванию класса, а затем по возрастанию возраста, сделать возраст своего рода первым, а затем сортировать снова используя класс:

Это замечательное свойство позволяет создавать сложные сортировки в несколько этапов. Например, чтобы отсортировать данные учащиеся по убыванию класса, а затем по возрастанию возраста, сделать возраст своего рода первым, а затем сортировать снова используя класс:

>>> s = sorted(student_objects, key=attrgetter('age'))     # sort on secondary key
>>> sorted(s, key=attrgetter('grade'), reverse=True)       # now sort on primary key, descending

Можно абстрагировать все это в функцию-оболочку, которая может принимать список и кортежи поля и упорядочивать их за нескольких проходах.

>>> def multisort(xs, specs):
...    for key, reverse in reversed(specs):
...        xs.sort(key=attrgetter(key), reverse=reverse)
...    return xs

>>> multisort(list(student_objects), (('grade', True), ('age', False)))

Функции модуля operator

Показанные выше шаблоны ключевых функций очень распространены, поэтому Python предоставляет удобные функции, упрощающие и ускоряющие функции доступа. Модуль имеет функции , и .

Используя эти функции, приведенные выше примеры становятся проще и быстрее:

>>> from operator import itemgetter, attrgetter

>>> sorted(student_tuples, key=itemgetter(2))


>>> sorted(student_objects, key=attrgetter('age'))

Функции модуля позволяют выполнять несколько уровней сортировки. Например, чтобы отсортировать по классу, а затем по возрасту:

>>> sorted(student_tuples, key=itemgetter(1,2))


>>> sorted(student_objects, key=attrgetter('grade', 'age'))

Сортировка методом Пузырька. Реализация алгоритма на языке Python.

Довольно часто при решении задач приходится сортировать значения в списке (массиве) по возрастанию или убыванию. Существует большое количество различных алгоритмов сортировки. Они отличается друг от друга временем выполнения (вычислительной сложностью), используемой памятью, а также сложностью в понимании и реализации.

Можете просмотреть следующее видео — изображающее принцип работы некоторых алгоритмов сортировки:

Один из самый простых алгоритмов сортировки, изучаемый в школьном курсе информатики — «Сортировка методом Пузырька». Его нельзя назвать быстрым, но он очень прост в понимании и реализации. Подходит для сортировки небольших списков (массивов).

Работу данного алгоритма представил в виде танца коллектив из Финляндии

  Как видно из видео процесс сортировки заключается в следующем:

1. Сравнивается i-ый элемент списка с i+1 — ым. Если больший из них имеет меньший порядковый номер, то они меняются местами (для сортировки по возрастанию)
2. Таким образом, самый большой элемент  сдвигается в конец списка
3. Далее процесс повторяется, но не до конца списка, а до последнего отсортированного элемента

Например:

Дан список (массив): 0, 5, 8, 4, 9, 3

Расположим элементы списка в процессе убывания. Т.е. если элемент меньше своего соседа справа — меняется с ним местами.

После первого прохождения по списку первый нолик становится на последнее место

Как можно заметить количество сравнений уменьшилось на единицу, так как число 0 — минимальное заняло свое законное место при первой итерации и сравнивать с ним нет смысла.

Продолжаем:

Последний шаг:

В итоге получаем отсортированный список:

Для списка из шести элементов достаточно выполнить  пять «проходов» по списку, поочередно сравнивая соседние элементы.

Напишем программу сортировки методом Пузырька на Python 3.

#создаем список
li = 
#вычисляем длину списка
n = len(li)
#внешний цикл отсчитывает количество "проходов" по списку
for j in range(0,n-1):
    #вложенный цикл сравнивает i-ый c i+1 -ым элементом и при необходимости меняет их местами
    #количество сравнений каждый раз уменьшается на величину j
    for i in range(0,n-j-1):
        if li < li:
            li,li = li, li
    print(j+1, "- ый проход цикла - ",end=" ")
    print(li)
print(li)

Задачи:

1. Отсортировать список по возрастанию суммы цифр чисел
2. Дан список целых чисел, состоящий из 30 элементов. Найти сумму пяти самых больших и пяти самых маленьких элементов списка.

Опубликовано в рубрике Программирование Метки: Python, алгоритмы, массив, программирование, Сортировка, Список

Сортировка сложных структур с использованием ключа

Это нормально работать с вещами, у которых по природе есть определенный порядок, вроде чисел или строк, но что делать с более сложными структурами? Здесь функция sorted() демонстрирует свое великолепие. Функция sorted() принимает ключ в качестве опционально названного параметра. Этот ключ должен быть, сам по себе, функцией, которая принимает один параметр, которая затем используется функцией sorted(), для определения значения в целях дальнейшей сортировки. Давайте взглянем на пример. Скажем, у нас есть класс Person с такими атрибутами как имя и возраст:

(Функция __repr__ является специальной функцией, которая используется для переопределения того, как объект будет представлен в интерпретаторе Python)

Причина, по которой я определил функцию – это выделение порядка сортировки. По умолчанию, представление определенных пользователем объектов выглядит примерно так: “<__main__.person object at>”. Если оставить все как есть, то отличать различные экземпляры в будущих примерах будет несколько затруднительно для нас.

Давайте сделаем список людей:

Сама по себе функция sorted() не знает, что делать со списком людей:

Однако, мы можем указать функции sorted(), какой атрибут сортировать, указав используемый ключ. Давайте определим это в следующем примере:

Функция ключа должна принять один аргумент и выдать значение, на котором базируется сортировка. Функция sorted() должна вызвать функцию key в каждом элементе используемой итерируемой, и использовать значение выдачи при сортировке списка.

Обратите внимание на то, что мы передаем ссылку на саму функцию, не вызывая ее и передаем ссылку к её возвращаемому значению. Это очень важный момент

Помните, sorted() будет использовать функцию key, вызывая её в каждом элементе итерируемой.

Давайте взглянем на еще один код, на этот раз определяем возраст как значение для сортировки:

Сравнение скоростей сортировок

Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.

Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.

Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.

Лучше понять эти алгоритмы вам поможет их визуализация.

Проверьте себя

Вернемся к набору данных .

Скачайте еще один набор данных: . Это можно сделать с помощью следующих двух строк в Jupyter Notebook:

Набор показывает всех пользователей, которые читают блог, а — тех, купил что-то в этом блоге за период с 2018-01-01 по 2018-01-07.

Два вопроса:

1. Какой средний доход в период с по от пользователей из ?
2. Выведите топ-3 страны по общему уровню дохода за период с по . (Пользователей из здесь тоже нужно использовать).

Решение задания №1

Средний доход —

Для вычисления использовался следующий код:

Краткое объяснение:

• На скриншоте также есть две строки с импортом pandas и numpy, а также чтением файлов csv в Jupyter Notebook.
• На шаге №1 объединены две таблицы ( и ) на основе колонки . В таблице хранятся все пользователи, даже если они ничего не покупают, потому что ноли () также должны учитываться при подсчете среднего дохода. Из таблицы удалены те, кто покупали, но кого нет в наборе . Все вместе привело к left-merge.
• Шаг №2 — удаление ненужных колонок с сохранением только .
• На шаге №3 все значения заменены на .
• В конце концов проводится подсчет с помощью .

Решение задания №2

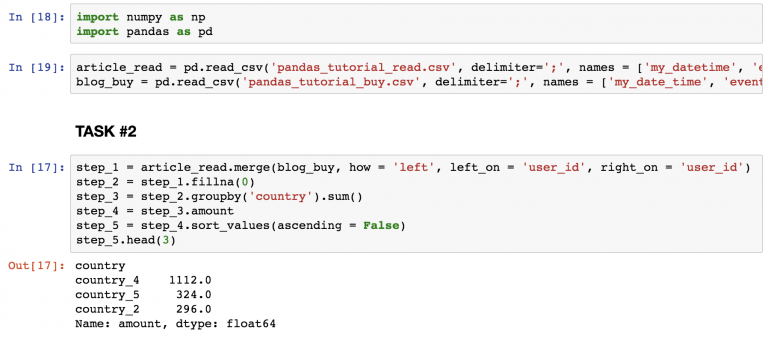
Найдите топ-3 страны на скриншоте.

Краткое объяснение:

1. Тот же метод , что и в первом задании.
2. Замена всех на .
3. Суммирование всех числовых значений по странам.
4. Удаление всех колонок кроме .
5. Сортировка результатов в убывающем порядке так, чтобы можно было видеть топ.
6. Вывод только первых 3 строк.

Delphi (сортировка произвольных типов данных — простое слияние)

unit uMergeSort;
 
interface
type
  TItem = Integer;               //Здесь можно написать Ваш произвольный тип
  TArray = array of TItem;
 
  procedure MergeSort(var Arr: TArray);
 
implementation
 
function IsBigger(d1, d2 : TItem) : Boolean;
begin
  Result := (d1 > d2);     //Сравниваем d1 и d2. Не обязательно так. Зависит от Вашего типа.
  //Сюда можно добавить счетчик сравнений
end;
 
//Процедура сортировки слияниями
procedure MergeSort(var Arr: TArray);
var
  tmp : TArray; //Временный буфер
  //Слияние
  procedure merge(L, Spl, R : Integer);
  var
    i, j, k : Integer;
  begin
    i := L;
    j := Spl + 1;
    k := 0;
    //Выбираем меньший из первых и добавляем в tmp
    while (i <= Spl) and (j <=R) do
    begin
      if IsBigger(Arr, Arr) then
      begin
        tmp := Arr;
        Inc(j);
      end
      else
      begin
        tmp := Arr;
        Inc(i);
      end;
      Inc(k);
    end;
    //Просто дописываем в tmp оставшиеся эл-ты
    if i <= Spl then      //Если первая часть не пуста
      for j := i to Spl do
      begin
        tmp := Arr;
        Inc(k);
      end
    else                  //Если вторая часть не пуста
      for i := j to R do
      begin
        tmp := Arr;
        Inc(k);
      end;
    //Перемещаем из tmp в arr
    Move(tmp, Arr, k*SizeOf(TItem));
  end;
 
  //Сортировка
  procedure sort(L, R : Integer);
  var
    splitter : Integer;
  begin
    //Массив из 1-го эл-та упорядочен по определению
    if L >= R then Exit;
    splitter := (L + R) div 2;  //Делим массив пополам
    sort(L, splitter);          //Сортируем каждую
    sort(splitter + 1, R);      //часть по отдельности
    merge(L, splitter, R);      //Производим слияние
  end;
 
  //Основная часть процедуры сортировки
begin
  SetLength(tmp, Length(Arr));
  sort(0, Length(Arr) - 1);
  SetLength(tmp, 0);
end;
 
end.

Стабильность сортировки и сложные сортировки в Python

Начиная с версии Python 2.2, сортировки гарантированно стабильны: если у нескольких записей есть одинаковые ключи, их порядок останется прежним. Пример:

Обратите внимание, что две записи с сохранили начальный порядок. Это свойство позволяет составлять сложные сортировки путём постепенных сортировок

Далее мы сортируем данные учеников сначала по возрасту в порядке возрастания, а затем по оценкам в убывающем порядке, чтобы получить данные, отсортированные в первую очередь по оценке и во вторую — по возрасту:

Алгоритмы сортировки Python вроде Timsort проводят множественные сортировки так эффективно, потому что может извлечь пользу из любого порядка, уже присутствующего в наборе данных.

6

Пузырьковая сортировка

Первым будет рассматриваться алгоритм пузырьковой сортировки, который требует порядка n*n перестановок, поэтому является не самым удачным выбором. В функции llist_bubble_sort, приведенной в листинге 1, выполняется вложенная итерация по списку, с помощью которой реализуется алгоритм пузырьковой сортировки для языка Си.

Листинг 1. Реализация пузырьковой сортировки на языке Си

#include <stdio.h>
#include <stdlib.h>

#define MAX 10

struct lnode 
{
 int data;
 struct lnode *next;
} *head, *visit;

void llist_add(struct lnode **q, int num);
void llist_bubble_sort(void);
void llist_print(void);

int main(void) 
{
 struct lnode *newnode = NULL;
 int i = 0;

 for(i = 0; i < MAX; i++) 
 {
   llist_add(&newnode, (rand() % 100));
 }

 head = newnode;
 printf("до пузырьковой сортировки:\n");
 llist_print();
 printf("после пузырьковой сортировки:\n");
 llist_bubble_sort();
 llist_print();

 return 0;
}

void llist_add(struct lnode **q, int num) 
{
 struct lnode *tmp; 
 
 tmp = *q;

 if(*q == NULL) {
  *q = malloc(sizeof(struct lnode));
   tmp = *q;
 } else {
  while(tmp->next != NULL)
   tmp = tmp->next;

   tmp->next = malloc(sizeof(struct lnode));
   tmp = tmp->next;
 }

 tmp->data = num;
 tmp->next = NULL;
}

void llist_print(void) 
{
 visit = head;

 while(visit != NULL) {
  printf("%d ", visit->data);
  visit = visit->next;
 }
 printf("\n");
}

void llist_bubble_sort(void) 
{
 struct lnode *a = NULL;
 struct lnode *b = NULL; 
 struct lnode *c = NULL;
 struct lnode *e = NULL; 
 struct lnode *tmp = NULL; 

 while(e != head->next) 
 {
	c = a = head;
	b = a->next;
		while(a != e) 
		{
			if(a->data > b->data) 
			{
				if(a == head) 
				{
					tmp = b -> next;
					b->next = a;
					a->next = tmp;
					head = b;
					c = b;
				} 
				else 
				{
					tmp = b->next;
					b->next = a;
					a->next = tmp;
					c->next = b;
					c = b;
				}
			} 
			else 
			{
				c = a;
				a = a->next;
			}
			b = a->next;
			if(b == e)
				e = a;
		}
	}
}

В листинге 2 приведена реализация пузырьковой сортировки на языке Python с использованием стандартных списков, встроенных в Python.

Листинг 2. Реализация пузырьковой сортировки на языке Python

import random 

lista = [] 

for i in range ( 0, 10 ) : 
  lista.append ( int ( random.uniform ( 0, 10 ) ) )

print lista
def bubble_sort ( lista ) :
  swap_test = False
  for i in range ( 0, len ( lista ) - 1 ):
    for j in range ( 0, len ( lista ) - i - 1 ):
      if lista > lista :
        lista, lista = lista, lista 
        swap_test = True
    if swap_test == False:
      break

bubble_sort ( lista ) 
print lista

В листинге 3 приведен исходный код пузырьковой сортировки для Python, но уже на основе связных списков.

Листинг 3. Пузырьковая сортировка с использованием связных списков

import random 

class Node:
    def __init__(self, value = None, next = None):
        self.value = value
        self.next = next

    def __str__(self):
        return 'Node '

class LinkedList:
    def __init__(self):
        self.first = None
        self.last  = None
        self.length = 0

    def add(self, x):
        if self.first == None:
            self.first = Node(x, None)
            self.last = self.first
        elif self.last == self.first:
            self.last = Node(x, None)
            self.first.next = self.last
        else:
            current = Node(x, None)
            self.last.next = current
            self.last = current

    def __str__(self):
        if self.first != None:
            current = self.first
            out = 'LinkedList \n'
        return 'LinkedList []'

    def BubbleSort(self):
       a = Node(0,None)
       b = Node(0,None)
       c = Node(0,None)
       e = Node(0,None)
       tmp = Node(0,None)
       
       while(e != self.first.next) :
        c = a = self.first
        b = a.next

        while a != e:
          if a and b:
            if a.value > b.value:
              if a == self.first:
                tmp = b.next
                b.next = a
                a.next = tmp
                self.first = b
                c = b
              else:
                tmp = b.next
                b.next = a
                a.next = tmp
                c.next = b
                c = b
            else:
              c = a
              a = a.next
            b = a.next
            if b == e:
              e = a
          else:
              e = a
              
    
L  = LinkedList()

for i in range ( 0, 10 ) : 
  L.add ( int ( random.uniform ( 0, 10 ) ) )

print L
L.BubbleSort()
print L

Как можно увидеть, код в листинге 3 очень похож на код на языке Си, приведенный в листинге 1, поскольку в Python работа со ссылками на объекты реализована практически так же, как и в языке Си.

Как работает Быстрая сортировка

Быстрая сортировка чаще всего не сможет разделить массив на равные части. Это потому, что весь процесс зависит от того, как мы выбираем опорный элемент. Нам нужно выбрать опору так, чтобы она была примерно больше половины элементов и, следовательно, примерно меньше, чем другая половина элементов. Каким бы интуитивным ни казался этот процесс, это очень сложно сделать.

Подумайте об этом на мгновение — как бы вы выбрали адекватную опору для вашего массива? В истории быстрой сортировки было представлено много идей о том, как выбрать центральную точку — случайный выбор элемента, который не работает из-за того, что «дорогой» выбор случайного элемента не гарантирует хорошего выбора центральной точки; выбор элемента из середины; выбор медианы первого, среднего и последнего элемента; и еще более сложные рекурсивные формулы.

Самый простой подход — просто выбрать первый (или последний) элемент. По иронии судьбы, это приводит к быстрой сортировке на уже отсортированных (или почти отсортированных) массивах.

Именно так большинство людей выбирают реализацию быстрой сортировки, и, так как это просто и этот способ выбора опоры является очень эффективной операцией, и это именно то, что мы будем делать.

Теперь, когда мы выбрали опорный элемент — что нам с ним делать? Опять же, есть несколько способов сделать само разбиение. У нас будет «указатель» на нашу опору, указатель на «меньшие» элементы и указатель на «более крупные» элементы.

Цель состоит в том, чтобы переместить элементы так, чтобы все элементы, меньшие, чем опора, находились слева от него, а все более крупные элементы были справа от него. Меньшие и большие элементы не обязательно будут отсортированы, мы просто хотим, чтобы они находились на правильной стороне оси. Затем мы рекурсивно проходим левую и правую сторону оси.

Рассмотрим пошагово то, что мы планируем сделать, это поможет проиллюстрировать весь процесс. Пусть у нас будет следующий список.

29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21,44 (high)

Выберем первый элемент как опору 29), а указатель на меньшие элементы (называемый «low») будет следующим элементом, указатель на более крупные элементы (называемый «high») станем последний элемент в списке.

29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21 (high),44

Мы двигаемся в сторону high то есть влево, пока не найдем значение, которое ниже нашего опорного элемента.

29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21 (high),44

• Теперь, когда наш элемент high указывает на элемент 21, то есть на значение меньше чем опорное значение, мы хотим найти значение в начале массива, с которым мы можем поменять его местами. Нет смысла менять местами значение, которое меньше, чем опорное значение, поэтому, если low указывает на меньший элемент, мы пытаемся найти тот, который будет больше.
• Мы перемещаем переменную low вправо, пока не найдем элемент больше, чем опорное значение. К счастью, low уже имеет значение 89.
• Мы меняем местами low и high:

29 | 21 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,99 (high),44

• Сразу после этого мы перемещает high влево и low вправо (поскольку 21 и 89 теперь на своих местах)
• Опять же, мы двигаемся high влево, пока не достигнем значения, меньшего, чем опорное значение, и мы сразу находим — 12
• Теперь мы ищем значение больше, чем опорное значение, двигая low вправо, и находим такое значение 41

Этот процесс продолжается до тех пор, пока указатели low и high наконец не встретятся в одном элементе:

29 | 21,27,12,19,28 (low/high),44,78,87,66,31,76,58,88,83,97,41,99,44

Мы больше не используем это опорное значение, поэтому остается только поменять опорную точку и high, и мы закончили с этим рекурсивным шагом:

28,21,27,12,19,29,44,78,87,66,31,76,58,88,83,97,41,99,44

Как видите, мы достигли того, что все значения, меньшие 29, теперь слева от 29, а все значения больше 29 справа.

Затем алгоритм делает то же самое для коллекции 28,21,27,12,19 (левая сторона) и 44,78,87,66,31,76,58,88,83,97,41,99,44 (правая сторона). И так далее.

Key Functions

Starting with Python 2.4, both list.sort() and sorted() added a key parameter to specify a function to be called on each list element prior to making comparisons.

For example, here’s a case-insensitive string comparison:

>>> sorted("This is a test string from Andrew".split(), key=str.lower)

The value of the key parameter should be a function that takes a single argument and returns a key to use for sorting purposes. This technique is fast because the key function is called exactly once for each input record.

A common pattern is to sort complex objects using some of the object’s indices as a key. For example:

>>> student_tuples = 
>>> sorted(student_tuples, key=lambda student: student)   # sort by age

The same technique works for objects with named attributes. For example:

>>> class Student:
        def __init__(self, name, grade, age):
                self.name = name
                self.grade = grade
                self.age = age
        def __repr__(self):
                return repr((self.name, self.grade, self.age))
        def weighted_grade(self):
                return 'CBA'.index(self.grade) / float(self.age)

>>> student_objects = 
>>> sorted(student_objects, key=lambda student: student.age)   # sort by age

Python 2.7 (функциональная реализация)

def merge(right, left, result):
    result.append((left if left < right else right).pop(0))
    return merge(right=right, left=left, result=result) if left and right else result+left+right
 
merge_sort = (lambda arr: arr if len(arr) == 1 else merge(merge_sort(arr[len(arr)/2:]),
                                                          merge_sort(arr[:len(arr)/2]), []))

 Недостатком сортировки слиянием является использование дополнительной памяти. Но когда работать приходиться с файлами или списками, доступ к которым осуществляется только последовательно, то очень удобно применять именно этот метод. Также, к достоинствам алгоритма стоит отнести его устойчивость и неплохую скорость работы O(n*logn).

При написании статьи были использованы открытые источники сети интернет :

Youtube 

Вывод

Объем алгоритма в исходнике примерно 2к строк и, как можно догадаться по описанию, код довольно запутанный. Зато за счет использования упорядоченности в реальных данных сложность Timsort в лучшем случае линейная. В худшем случае, если входные данные случайные, timsort справится за O(n log n), а это неплохо для сортировки. Кстати, несмотря на то, что Timsort изначально был придуман в Python-сообществе, сейчас он используется еще в Java, Swift и Android platform.

Вот что нужно запомнить о Timsort:

• Timsort это гибридный алгоритм сортировки, сочетающий модифицированные варианты сортировки вставками и сортировки слиянием;
• Timsort пользуется тем, что реальные данные часто бывают частично упорядочены;
• В лучшем случае сложность O(n), в худшем — O(n log n)).

Визуализацию работы алгоритма можно посмотреть здесь:

Видно, как сначала строятся run’ы и как они сливаются

Обратите внимание, что в обоих прогонах всегда объединяются примерно равные по размеру части

Заключение

Метод пузырька гораздо менее эффективен других алгоритмов, однако он имеет простую и понятную реализацию, поэтому часто используется в учебных целях. Кроме того, пузырьковая сортировка может использоваться для работы с небольшими массивами данных.

На самом деле, вместо самостоятельного написания алгоритмов сортировки программисты на Python используют стандартные функции и методы языка, такие как и . Эти функции отлажены и работают быстро и эффективно.

Знания особенностей алгоритмов сортировки, их сложности и принципов реализации в общем виде пригодятся каждому программисту, желающему пройти собеседование и стать Python-разработчиком.