Как перевести дробь в десятичную и наоборот

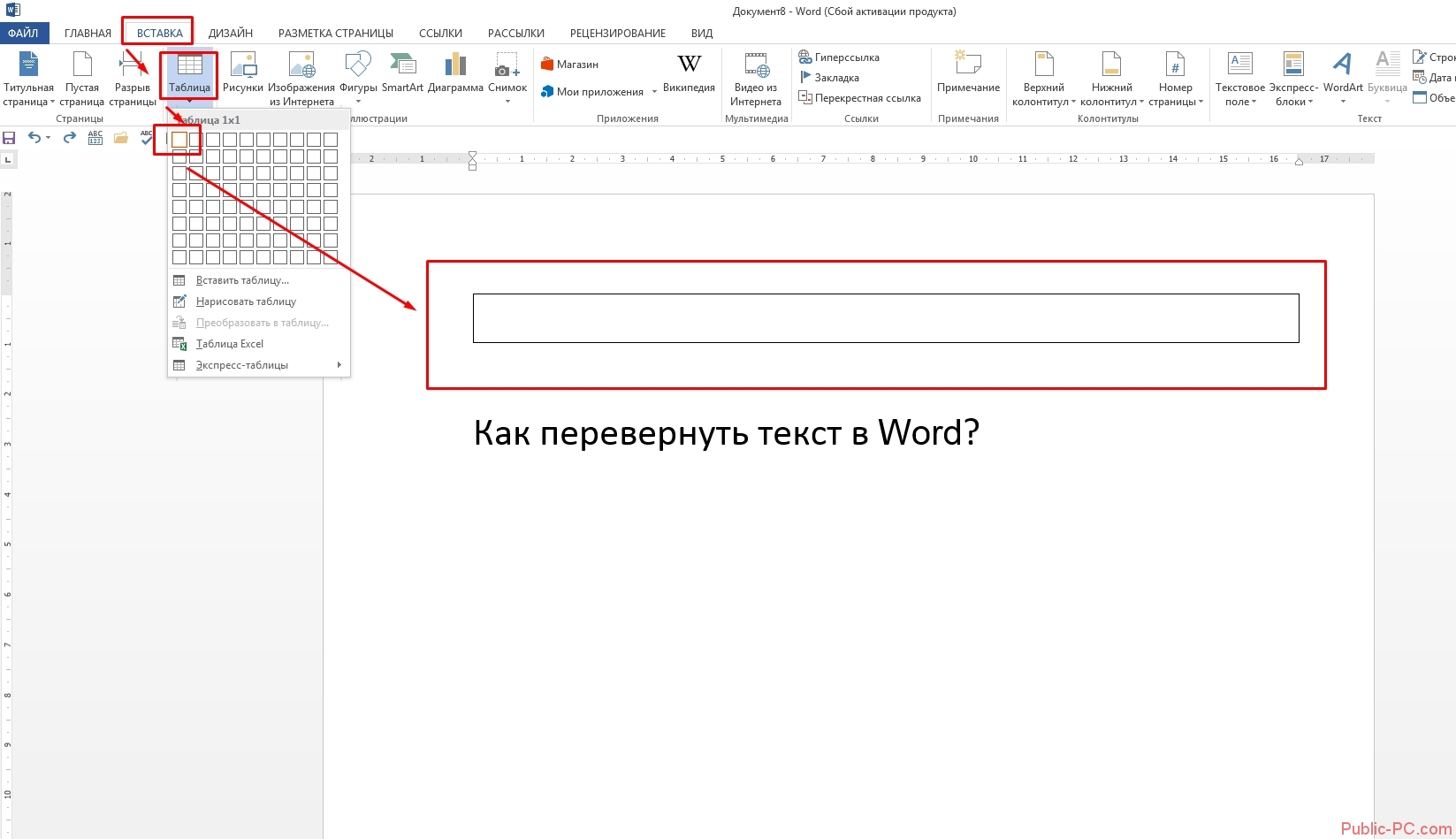
Как сделать дробь в Ворде

Написать дробь в Word можно, используя слеш – «/» . Но это подойдет только тем, у кого нет особых требований к оформлению текста. Если нужно поставить правильную дробь в тексте, то воспользуемся в этом случае вставкой формулы.

Установите курсор в нужном месте документа, где будет стоять дробь. Теперь откройте «Вставка» – «Формула» , как было описано в пункте выше. В структурах кликните по кнопочке «Дробь» и выберите из меню нужный вид дроби.

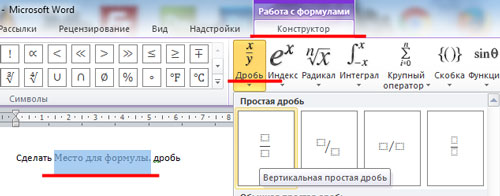
Заполните пустые квадратики значениями.

Если Вы хотите вставить в текст диагональную простую дробь – «½» , перейдите на вкладку «Вставка» , кликните там по кнопочке «Символ» , и перейдите в «Другие символы» .

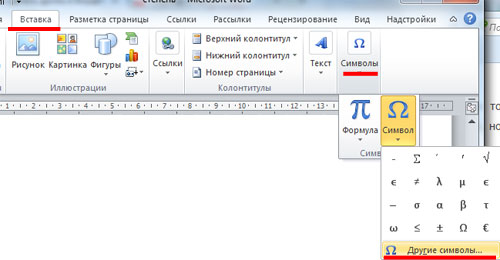
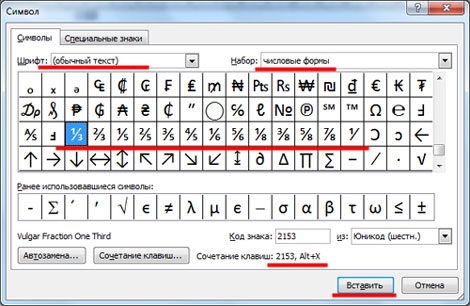
В поле «Шрифт» выберите «(обычный текст)» , в поле «Набор» – «числовые формы» . Здесь вы увидите различные дроби. К сожалению, выбор ограничен, и вставить в текст можно только дробь с теми числами, которые есть в списке. Выделите нужную и нажмите на кнопочку «Вставить» .

Обратите также внимание на сочетание клавиш. Например, чтобы вставить в текст дробь «⅓» , нужно набрать комбинацию цифр «2153» и нажать сочетание клавиш «Alt+X»

Как видите, поставить степень или написать дробь определенного вида, в нужном Вам документе Ворд, не так уж и сложно.

Дроби в «Ворде» встречаются довольно часто. Они могут пригодиться при написании рецептов или формул в точных науках. К сожалению, вставить знак дроби не всегда легко. Существуют разные варианты развития событий. Ниже будет рассказано о том, как справиться с поставленной задачей. Каким образом юзеры пишут дроби? Как облегчить себе жизнь?

Вид №3: горизонтальная дробь

Более привычный для нас вариант, который часто встречается в публицистических и научно-популярных статьях – это горизонтальная дробь.

Горизонтальную дробь можно ввести четырьмя способами:

• Вставка->Формула->Дробь->Горизонтальная простая дробь;
• Вставка->Символ->Числовые формы;В данном случае удобно осуществлять повторный ввод дробей —  с помощью панели «Ранее использовавшиеся символы». Если вышеперечисленные дроби используется часто, можно настроить комбинации «горячих клавиш» или параметры автозамены.                                                                                       
• Вставка->Объект-> Microsoft Equation 3.0->Шаблоны дробей и радикалов.
• слэш

Самый простой и быстрый способ изобразить дроби,  не прибегая к вставкам – использовать «слэш» (или косую черту, наклоненную вправо) на клавиатуре. Именно так поступает большинство пользователей Интернета, которые не желают тратить время на поиск нужных символов. Конечно же, для тех, кто занят написанием серьезных научных работ, лучше выбрать специальные изображения дробей.

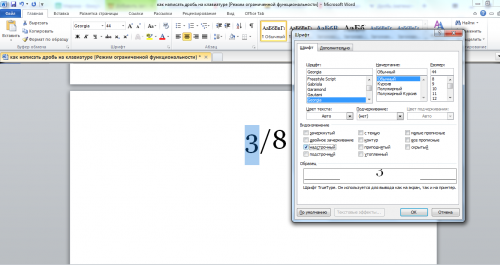
Слэш располагается на клавиатуре в следующих местах:

• Рядом с правой кнопкой Shift на английской раскладке;
• В цифровом блоке;
• Над и слева от Enter (необходимо нажимать одновременно с Shift).

Вы также можете набрать слэш следующим образом:

1. Включите кнопку NumLock;
2. Зажмите Alt и наберите на цифровой клавиатуре 4 и затем 7;
3. Отпустите Alt.

Чтобы дробь, записанная через слэш, смотрелась естественнее, можно использовать следующую последовательность:

1. Выделить числитель дроби->Шрифт->Видоизменение->Надстрочный (ставим галочку) ->ОК;
2. Выделить знаменатель дроби->Шрифт->Видоизменение->Подстрочный (ставим галочку) -> ОК.

Теперь вы знаете, как написать дробь на клавиатуре. Как видите, это можно сделать самыми разными способами, и каждый из них достаточно прост. Желаем вам успехов в дальнейшем освоении компьютерной грамоты!

Lifeo.ru

Предыдущая:Что будет, если съесть грифель от карандаша? Последствия
Дальше:Как научить собаку команде «Фу»: пошаговая инструкция

Голос за пост — плюсик в карму! 🙂

Вставка символов

Как записать дробь в «Ворде»? Более приемлемым способом является вставка специального символа с той или иной записью. Недостатком этого приема является то, что записать в текстовом редакторе удастся не все дробные числа.

Чтобы вставить дробь-символ, нужно выполнить такие манипуляции:

Зайти в «Таблицу символов» Windows. Служба находится в пункте меню «Служебные» в «Пуске».
Пролистать список символов почти до конца при шрифте «Таймс Нью Роман».
Выделить курсором ту или иную дробь.
Щелкнуть по кнопке «Выбрать», а затем по элементу «Копировать».

Теперь можно вставить скопированный символ в «Ворд» любым известным способом. Никаких затруднений с приемом быть не должно.

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Запоминаем

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю, а затем сравнить числители.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

• Нужно подобрать число, которое будет делиться на 7 и на 2 (найти наименьшее общее кратное НОК). В данном случае, НОК — 14. Проверим:
  14:7 = 2
  14 : 2 = 7
• Первую дробь умножаем на дополнительный множитель 2:
• Вторую дробь умножаем на дополнительный множитель 7:
• Дроби приведены к общему знаменателю:

Давайте потренируемся в сравнении дробей. 

Пример 1. Сравните дроби:

• Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
  30 : 15 = 2
  30 : 2 = 15
• Первую дробь умножаем на дополнительный множитель 2:
• Вторую дробь умножаем на дополнительный множитель 15:
• Дроби приведены к общему знаменателю:
• Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

• 6/5 — неправильная дробь. 
• Выделим целую часть:
• Значит, что

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого. 

12 — 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы». 

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
 

Пример 1. Найдите разность:

Вычитаемая дробь меньше уменьшаемой

Выполняем вычитание:

Пример 2.Найдите разность:

• Смешанные дроби превращаем в неправильные:
• Чтобы сравнить дроби с разными числителями и знаменателями, нужно привести их к общему знаменателю:
• Наименьшее общее кратное — 40
  40 : 8 = 5
  40 : 5 = 8
• Умножаем первую дробь на дополнительный множитель 5:
• Умножаем вторую дробь на дополнительный множитель 8:
• Дроби приведены к общему знаменателю:

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Мы видим, что вычитаемое меньше уменьшаемого, значит можем без труда найти разность:

Деление посредством знака «Слеш/»

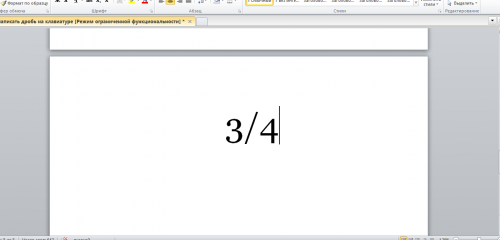
Помимо привычного горизонтального вида дробей, встречается и вертикальное деление в виде слеша, например: 1/2. Данный способ работает во всех версиях Ворда с 2003 по 2016. Найти и вставить символ можно следующим образом.

Вариант 1: С помощью кнопки «?/»

1. Переключить с русского метода ввода слов на английский: сочетание клавиш «Shift+Alt» либо «Windows+пробел»;
2. Установить курсор мыши на место, где нужно поставить дробную черту;
3. Нажать кнопку правее от буквы «Ю».
4. Напечатать необходимое значение делителя.

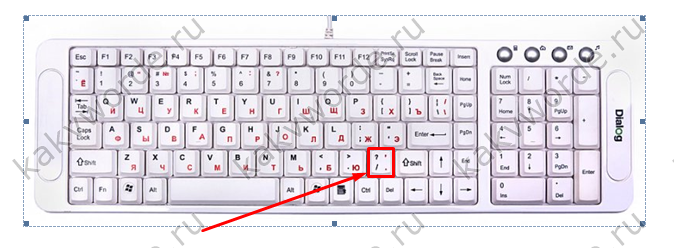
Вот готовый результат, как можно еще заменить знак деления.

Вариант 2: посредством функции «Символ»

Чтобы написать дробь простую и по диагонали, используйте:

Вкладка «Вставка» – «Символ» – «Другие символы».Внимание! В секции «Шрифт» должен быть «Обычный текст», а в секции «Набор» – «Числовые формы». В ином случае вставить диагональную дробь не получится.
После правильной настройки, выбрать соответствующее дробное число и нажать вставить

Вариант 3. Код знака

На картинке ниже видно, что вставить обыкновенную дробь можно и с помощью сочетания клавиш, зная код знака. В нашем случае пишем код знака 215B и удерживая Alt нажимаем на X (английская).

Вот мы и рассмотрели все варианты написания дроби и самой дробной черты.

Работа с формулами в Ворде, кому и зачем это надо

Здравствуйте друзья! Текстовый редактор Word имеет много полезных функций и инструментов, которые помогают сделать ту или иную работу достаточно быстро. Например, Вам нужно написать контрольную (научную, дипломную) работу по алгебре, геометрии, химии, физике, работу по другим предметам. В этих работах часто пишут формулы. Вам придется писать формулы в программе Ворд, если Вы делаете курсовую или дипломную работу на заказ.

Работа с формулами в Ворде нужна в основном студентам, школьникам и тем, кто зарабатывает через Интернет с помощью Word. Иногда формулы встречаются в статьях на сайтах и блогах. Как писать формулы в Ворд быстро? На данный вопрос стоит ответить, поскольку это надо знать студентам, школьникам и тем, кто зарабатывает через Интернет с помощью Ворда. По инструкции, Вы сможете написать любую формулу, без особых затруднений.

Написание цифр через дробь

Редактор Word предоставляет возможность автоматического преобразования нескольких цифр с наклонной чертой (слеш или дробь) между ними в одиночный символ дробного числа. Например, если ввести цифры 1⁄2 или 1⁄4, то они автоматически преобразуются в соответствующие числовые формы с изменением размера шрифта и его смещением вверх (для числителя) и вниз (для знаменателя).

Следует оговориться, что такое автоматическое преобразование возможно лишь в случае, если в диалоговом окне Параметры автозамены на вкладке Автоформат при вводе у вас установлен флажок на параметре Заменять при вводе дроби соответствующими знаками.

Но что делать, если необходимо ввести иные цифры и представить их в виде дробей (например, номер дома 21⁄4)?

Если вы планируете вставлять такие простые дроби, как 1⁄3, 2⁄3, 1⁄8, 5⁄8, 7⁄8, то это можно сделать с помощью диалогового окна Символы, открываемого с помощью команды Символ из меню Вставка.

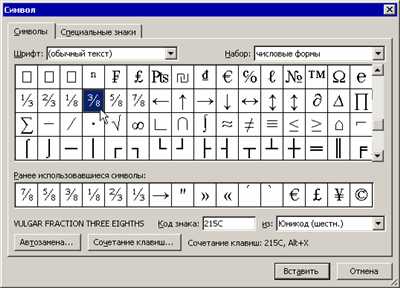
Если же нужно вставлять более сложные варианты, то есть два варианта: вручную форматировать цифры или использовать небольшой макрос.

Чтобы вручную отформатировать цифры, выполните следующие действия.

Введите числа с наклонной чертой, например, 21⁄4.

Выделите числитель и видоизмените его на надстрочный шрифт (меню Формат – Шрифт – Надстрочный) или воспользуйтесь сочетанием клавиш «Ctrl»+«Shift»+«+=».

Выделите знаменатель и видоизмените его на подстрочный шрифт (меню Формат – Шрифт – Подстрочный) или воспользуйтесь сочетанием клавиш «Ctrl»+«+=».

Чтобы автоматизировать процесс форматирования чисел с дробями можно воспользоваться следующим макросом (на основе макроса от Allen Wyatt).

Sub fraction() Dim rFraction As Range Dim iSlash As Integer With Selection iSlash = InStr(RTrim(.Text), «/») Set rFraction = ActiveDocument.Range (Start:=.Start, End:=.Start + iSlash – 1) rFraction.Font.Superscript = True Set rFraction = ActiveDocument.Range (Start:=.Start + iSlash, End:=.End) rFraction.Font.Subscript = True End With Selection.Collapse direction:=wdCollapseEnd Selection.Font.Subscript = False End Sub

Выделите цифры (содержащие наклонную черту) и запустите макрос.

Существует и другой способ написания дробей – через горизонтальную линию – с помощью кодов полей.

Выполнение действий со смешанными дробями, формулы и примеры

Сложение

Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.

Формульное выражение сложения смешанных чисел:

\(a\frac bc+d\frac ef=\left(a+d\right)+\left(\frac bc+\frac ef\right)\)

Пример:

\(2\frac13+5\frac47\;\)

Вычисляем наименьший общий знаменатель дробных слагаемых:

3×7=21

\(2\frac13+5\frac47=2+5+\frac13+\frac47\;=7+\frac7{21}+\frac{12}{21}=7+\frac{7+12}{21}=7\frac{19}{21}\)

Вычитание

Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.

Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:

\(a\frac bc-d\frac ef=\left(a+\frac bc\right)-\left(d+\frac ef\right)\;=\left(a-d\right)+\left(\frac bc-\frac ef\right)\)

В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:

\(a\frac bc-d\frac ef=\left(\left(a-d\right)-\frac ef\right)+\frac bc\)

Пример:

\(13\frac38-6\frac12\)

Для решения этого выражения найдем наименьший общий знаменатель:

8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.

\(13\frac38-6\frac12=13\frac38-6\frac48=\left(12+1+\frac38\right)-6\frac48=\left(12+\frac{1\times8+3}8\right)-6\frac48=12\frac{11}8-6\frac48=\left(12-6\right)+\left(\frac{11}8-\frac48\right)=6+\frac{11-4}8=6\frac78\)

Умножение и деление

Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.

Формула умножения смешанных чисел выглядит так:

\(a\frac bc\times d\frac ef=\frac{a\times c+b}c\times\frac{d\times f+e}f=\frac{\left(a\times c+b\right)\times\left(d\times f+e\right)}{c\times f}=\frac{\left(ac+b\right)\left(df+e\right)}{cf}\)

Формула деления смешанных дробей:

\(a\frac bc\div d\frac ef=\frac{a\times c+b}c\div\frac{d\times f+e}f=\frac{a\times c+b}c\times\frac f{d\times f+e}=\frac{\left(a\times c+b\right)\times f}{c\times\left(d\times f+e\right)}=\frac{f\left(ac+b\right)}{c\left(df+e\right)}\)

Пример 1:

\(5\frac2{19}\times2\frac79=\frac{5\times19+2}{19}\times\frac{2\times9+7}9=\frac{97}{19}\times\frac{25}9=\frac{97\times25}{19\times9}=\frac{2425}{171}=14\frac{31}{171}\)

Пример 2:

\(4\frac23\div3\frac57=\frac{4\times3+2}3\div\frac{3\times7+5}7=\frac{14}3\div\frac{26}7=\frac{14}3\times\frac7{26}=\frac{14\times7}{3\times26}=\frac{98}{78}=\frac{98\div2}{78\div2}=\frac{49}{39}=1\frac{10}{39}\)

При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно. Такого рода вычисления производятся с помощью распределительного закона умножения.

Пример 3:

\(3\frac56\times4=\left(3+\frac56\right)\times4=3\times4+\frac56\times4=12+\frac{5\times4}6=12+\frac{20\div2}{6\div2}=12+\frac{10}3=12+3\frac13=15\frac13\)

Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.

Пример 4:

\(5\div3\frac27=\frac51\div\frac{3\times7+2}7=\frac51\div\frac{23}7=\frac51\times\frac7{23}=\frac{5\times7}{1\times23}=\frac{35}{23}=1\frac{12}{23}\)

Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.

Пример 5:

2Приведение к общему знаменателю

Чтобы произвести действие вычитания из целого числа дробного данным способом, необходимо уменьшаемое и вычитаемое привести к общему знаменателю.

• Записываете действие вычитания двух выражений в виде единого дробного выражения, знаменателем которого будет знаменатель дроби-вычитаемого.
• В числителе же будет записана разность между целым числом (уменьшаемым), умноженным на знаменатель дроби, и числителем дроби.
• Выполняете действие вычитания в числителе записанного выражения.
• При необходимости в получившемся дробном выражении выделяете целую часть.

По желанию можно не объединять два выражения в одно. В этом случае необходимо:

• Представить целое число в виде дроби, числитель которой и есть данное число, а знаменатель равен 1.
• Далее умножаете числитель и знаменатель полученной дроби на знаменатель дроби-вычитаемого.
• Производите действие вычитания для двух дробных выражений с одинаковым знаменателем – переписываете общий знаменатель, а в числителе выполняете вычитание.

Что делать с целой частью

На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.

Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:

\

Затем вспоминаем про «утерянную» единицу и дописываем её спереди:

\

Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:

\

В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)

В заключение хотел бы рассмотреть ещё один приём, который многим помогает.

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

1% = 1/100 = 0,01

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Быстрая напоминалка:

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Ответ: 5,4 = 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

Как решаем:

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Как отключить автозамену знака «Деления»

Чтобы текстовый редактор Ворд не делал автозамену при вводе дробного числа, нужно отключить данную функцию в настройках. Выполните следующие действия:

Для работы с текстовыми документами, таблицами и формулами используется такая программа, как Word. Это многофункциональная программа, которая позволяет производить множество манипуляций с текстом, а также добавлять в него множество значков и изображений. Для составления текстовых документов математического характера часто необходимо вставить в текст дроби, причем правильно заполненные. Но многие пользователи не представляют, как это сделать и задают вопрос, как в ворде написать дробь. Чтобы разобраться в этом вопросе, необходимо рассмотреть весь алгоритм проведения этой манипуляции:

Самым простым способом для осуществления этой вставки является простое написание числителя, и после подчеркивания написания знаменателя в следующей строке. Чтобы удобнее это сделать необходимо зайти во вкладку «Вставка» и там выбрать функцию «Надпись». Удобство этой манипуляции заключается в том, что таким образом можно установить интервалы между строками, для этого надо зайти в меню «Формат» и выбрать там опцию «Абзац», такая мера позволит представить дробь естественно и визуально.

Следующим способом создать дробь в документе Word седьмой или десятой редакции, является следующий алгоритм действий:

• нужно открыть документ, в котором будут происходить изменения
• потом поставить курсор туда, где будет дробь
• перейти в меню «Вставка» и там выбрать опцию «Формула»
• в этой вкладке выбрать необходимый вид формулы

Если необходимо вставить дробь в документ, созданный в программе Word третьей версии, то следует действовать по такому принципу:

• нужно найти в приборной панели специальную стрелочку, при нажатии на которую будет открываться активное окошко «Параметры панелей инструментов»
• нужно кликнуть по ней левой кнопкой мыши и выбрать там «Добавить или удалить кнопки»
• дальше выбрать вкладку «Настройки»:
• после этого нужно перейти в активное окошко «Команды»
• выбрать в левом столбике опцию «Вставка»
• найти там функцию «Редактор формул»:
• в «Редакторе формул» левой кнопкой мыши зажать надпись и перетащить ее на необходимое место в панели управления:
• на заключительном этапе нудно кликнуть по появившейся иконке «Редактор формул»
• в открывшемся активном окне выбрать «Шаблон дробей и радикалов» и подобрать необходимый внешний вид дроби
• в заштрихованную рамку нужно вставить ваши числа
• после этого кликнуть в пустом месте экрана и дробь готова.

Следует рассмотреть подобную ситуацию в программе Word седьмой версии, она немного отличается от той, что описана выше.

1. Итак, сначала нужно открыть документ, в котором вы собираетесь работать и навести курсор мыши на то место, где будет стоять дробь.
2. После этого нужно перейти во вкладку «Вставка» и там выбрать опцию «Формула»:
3. Откроется новое активное окно «Конструктор» и в нем есть большое количество математических знаков и формул, в которые можно подставлять значения. Там нужно найти «Дробь» и кликнуть по ней левой клавишей мыши:
4. Появятся окошки с разными знаками и там мы выбираем нужную нам дробь:
5. После того, как вы это проделаете в документе, в том месте, где стоял курсор, появится дробь.
6. Теперь ее необходимо заполнить значениями, то есть ввести числитель и знаменатель. Кроме того, и в знаменатель и в числитель можно добавить еще одну дробь:

Для работы с математическими документами в Ворде представлен большой функционал и при желании можно выполнить задание любой сложности. Так Ворд предлагает не только вводить в текст дроби, но и целые готовые формулы, куда надо лишь подставить значения. Поэтому не стоит пренебрегать этими функциями и дорисовывать дроби вручную в готовой работе, нужно просто немного внимательнее изучить работу программы.

В целом можно сказать, что ни чего сложного в этом вопросе нет

Необходимо только соблюдать внимание и не торопится. Надо отметить, что программа Word, с каждой новой версии наполняется различными столь необходимыми функциями, что ее популярность не падает в течение многих лет

Поэтому если возникают сложности с работой в документах не стоит отчаиваться, надо просто внимательно изучить функционал этой замечательной программы.

Редактирование текстовых документов вызывает у пользователей немало вопросов. Их не может избежать даже продвинутый юзер, ведь знать все невозможно. Поэтому иногда приходится изучать те или иные секреты. Ниже постараемся выяснить, как написать дробь на клавиатуре и не только. Все манипуляции будут рассмотрены на примере текстового редактора Microsoft Word. С ним работает основная масса юзеров.

Выражение величин в дробном виде

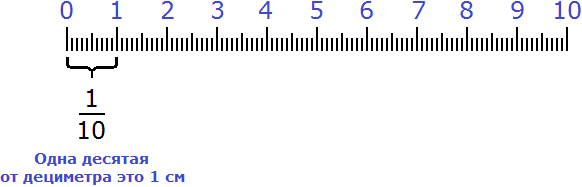
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:

Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:

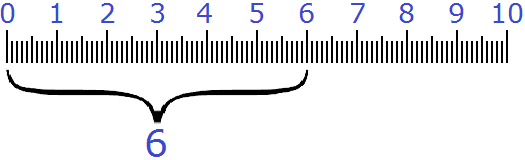
Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.

Итак, 6 целых сантиметров у нас уже есть:

Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см

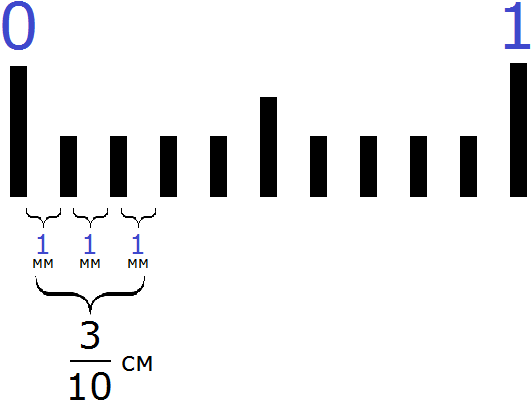
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.

В результате имеем шесть целых сантиметров и три десятых сантиметра:

Цифра 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».

Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.

Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6

6

Целая часть записана. Сразу же после написания целой части ставим запятую:

6,

И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:

6,3

Любое число, которое представляется в таком виде, называется десятичной дробью.

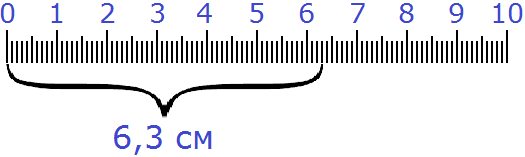
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:

6,3 см

Выглядеть это будет следующим образом:

На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1000 или 10000.

Как и смешанное число, десятичная дробь имеет цéлую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .

В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.

Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:

0,5

Читается как «ноль целых, пять десятых».

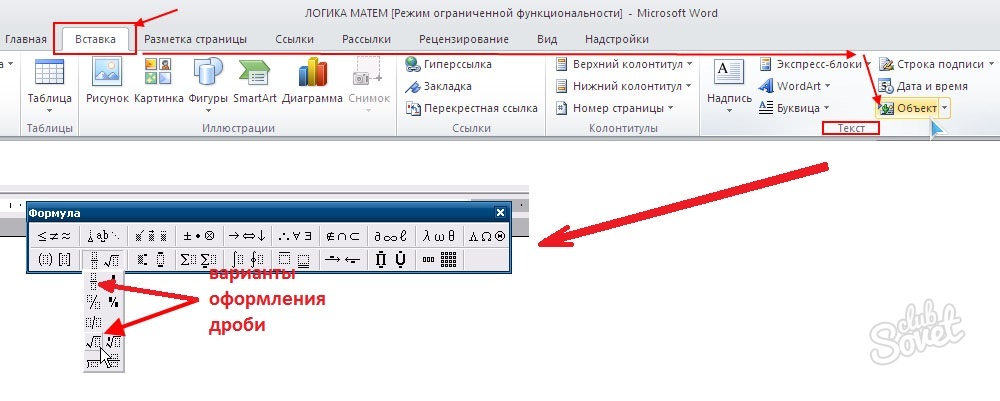
Пишем дробь с горизонтальным разделителем

Мы уже знаем, как в «Ворде» сделать дробь со слешем, теперь же поговорим о том, как использовать в качестве разделителя горизонтальную линию. Для этого вам понадобится:

Запустить программу Microsoft Word, перейти во вкладку «Вставка», где в правой части на панели инструментов следует нажать уже по знакомому выпадающему списку «Символы».
В выпадающем меню выбрать пункт «Уравнение», обозначающийся символом «пи»

Обратите внимание, если вы используете старую версию программы, то этот элемент называется «Формулы».
Откроется меню, в котором вам необходимо нажать кнопку «Вставить новое уравнение».
Появится дополнительная вкладка под названием «Конструктор». Среди перечня инструментов выберите «Дробь».
В меню найдите тот формат написания дроби, который вам необходим.
В тексте, где был установлен курсор, появится форма для заполнения с выбранным вариантом дроби

Вам необходимо вписать в соответствующие поля нужные значения.

Теперь вы знаете и второй способ, как в «Ворде» сделать дроби. Как вы можете заметить, первый вариант позволяет писать число только через слеш, в то время как во втором можно использовать различные типы разделителя. Каким способом пользоваться удобнее – решать только вам.