Как печатать дроби на клавиатуре

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

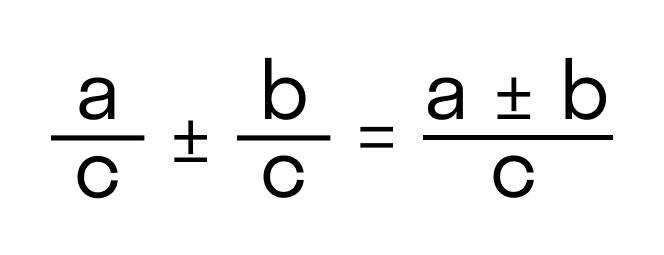
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

1. Найдем наименьшее общее кратное для определения единого делителя.

   Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

   НОК (15, 18) = 3 * 2 * 3 * 5 = 90

2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

   90 : 15 = 6,

   90 : 18 = 5.

   Полученные числа запишем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
   • если делимое больше делителя, нужно преобразовать в смешанное число;
   • если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

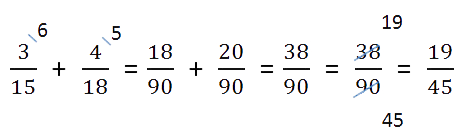
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.
2. Сложить дробные части.

   Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

3. Суммировать полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

История и этимология термина

Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Фундамент теории обыкновенных дробей заложили греческие и индийские математики. Через арабов термин, в переводе на латинский, перешёл в Европу, он упоминается уже у Фибоначчи (1202 год). Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.

Дроби вычислялись ещё в Древнем Египте. До наших дней сохранились математические источники о египетских дробях: Математический папирус Ринда (ок. 1650 год до н. э.), Египетский математический кожаный свиток (XVII век до н. э.), Московский математический папирус (ок. 1850 год до н.э.), Деревянная табличка из Ахмима (англ.) (ок. 1950 год до н.э.).

В Китае обыкновенные дроби встречаются в труде «Математика в девяти книгах» (X-II в до н. э.), отредактированной во II в до н. э. финансовым чиновником Чжан Цаном . Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную. Персидский математик и астроном Джамшид Гияс-ад-дин ал-Каши (1380—1429) в трактате «Ключ арифметики» (1427 г.) объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на пять веков раньше.

Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Современное обозначение обыкновенных дробей происходит из — вначале его позаимствовали арабы, а затем, в XII-XVI веках, — европейцы. Вначале в дробях не использовалась дробная черта: числа 14,215{\displaystyle {\tfrac {1}{4}},2{\tfrac {1}{5}}} записывались таким способом: 14,2I5.{\displaystyle {\begin{smallmatrix}1\\4\end{smallmatrix}},{\begin{smallmatrix}2\\\mathrm {I} \\5\end{smallmatrix}}.} Использование черты дроби стало постоянным лишь около 300 лет назад. В Европе первым учёным, который использовал и распространял индийскую систему счёта (известную как «арабские цифры»), в том числе способ записи дробей, стал итальянский купец, путешественник, сын городского писаря — Фибоначчи (Леонардо Пизанский). Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).

В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585). Стевин записывал десятичные дроби сложными способами: например, число 42,53 записывалось как 42 51 32{\displaystyle {\overset {\underset {0}{}}{4}}2~{\overset {\underset {1}{}}{5}}~{\overset {\underset {2}{}}{3}}} или 42 ⓪ 5 ① 3 ②, где в круге или над строкой означал целую часть, 1 — десятые, 2 — сотые, и так далее. Запятую для отделения целой части стали использовать с XVII века.

На Руси дроби называли долями. В первых российских учебниках математики — в XVII веке — дроби назывались ломаными числами. Термин дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.

Пишем дробь с горизонтальным разделителем

Мы уже знаем, как в «Ворде» сделать дробь со слешем, теперь же поговорим о том, как использовать в качестве разделителя горизонтальную линию. Для этого вам понадобится:

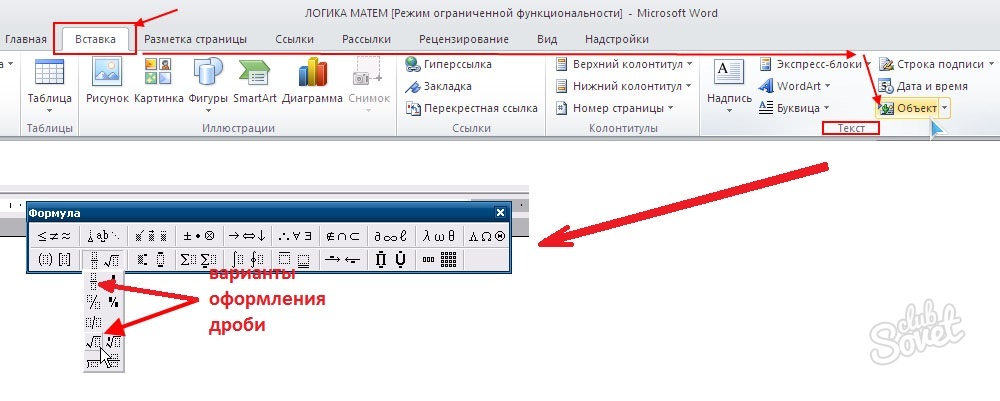
Запустить программу Microsoft Word, перейти во вкладку «Вставка», где в правой части на панели инструментов следует нажать уже по знакомому выпадающему списку «Символы».
В выпадающем меню выбрать пункт «Уравнение», обозначающийся символом «пи»

Обратите внимание, если вы используете старую версию программы, то этот элемент называется «Формулы».
Откроется меню, в котором вам необходимо нажать кнопку «Вставить новое уравнение».
Появится дополнительная вкладка под названием «Конструктор». Среди перечня инструментов выберите «Дробь».
В меню найдите тот формат написания дроби, который вам необходим.
В тексте, где был установлен курсор, появится форма для заполнения с выбранным вариантом дроби

Вам необходимо вписать в соответствующие поля нужные значения.

Теперь вы знаете и второй способ, как в «Ворде» сделать дроби. Как вы можете заметить, первый вариант позволяет писать число только через слеш, в то время как во втором можно использовать различные типы разделителя. Каким способом пользоваться удобнее – решать только вам.

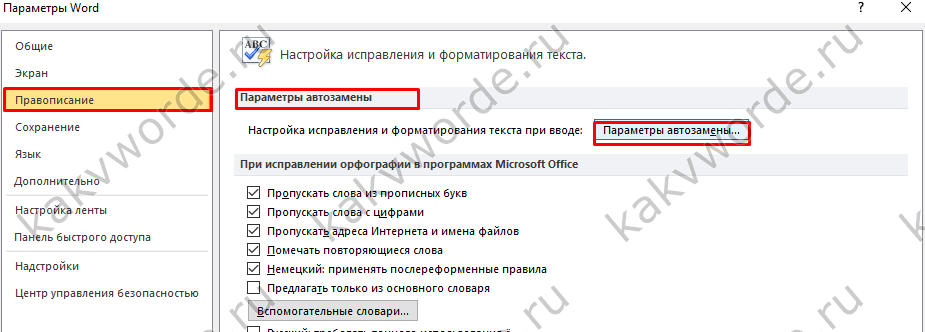
Как отключить автозамену знака «Деления»

Чтобы текстовый редактор Ворд не делал автозамену при вводе дробного числа, нужно отключить данную функцию в настройках. Выполните следующие действия:

Для работы с текстовыми документами, таблицами и формулами используется такая программа, как Word. Это многофункциональная программа, которая позволяет производить множество манипуляций с текстом, а также добавлять в него множество значков и изображений. Для составления текстовых документов математического характера часто необходимо вставить в текст дроби, причем правильно заполненные. Но многие пользователи не представляют, как это сделать и задают вопрос, как в ворде написать дробь. Чтобы разобраться в этом вопросе, необходимо рассмотреть весь алгоритм проведения этой манипуляции:

Самым простым способом для осуществления этой вставки является простое написание числителя, и после подчеркивания написания знаменателя в следующей строке. Чтобы удобнее это сделать необходимо зайти во вкладку «Вставка» и там выбрать функцию «Надпись». Удобство этой манипуляции заключается в том, что таким образом можно установить интервалы между строками, для этого надо зайти в меню «Формат» и выбрать там опцию «Абзац», такая мера позволит представить дробь естественно и визуально.

Следующим способом создать дробь в документе Word седьмой или десятой редакции, является следующий алгоритм действий:

• нужно открыть документ, в котором будут происходить изменения
• потом поставить курсор туда, где будет дробь
• перейти в меню «Вставка» и там выбрать опцию «Формула»
• в этой вкладке выбрать необходимый вид формулы

Если необходимо вставить дробь в документ, созданный в программе Word третьей версии, то следует действовать по такому принципу:

• нужно найти в приборной панели специальную стрелочку, при нажатии на которую будет открываться активное окошко «Параметры панелей инструментов»
• нужно кликнуть по ней левой кнопкой мыши и выбрать там «Добавить или удалить кнопки»
• дальше выбрать вкладку «Настройки»:
• после этого нужно перейти в активное окошко «Команды»
• выбрать в левом столбике опцию «Вставка»
• найти там функцию «Редактор формул»:
• в «Редакторе формул» левой кнопкой мыши зажать надпись и перетащить ее на необходимое место в панели управления:
• на заключительном этапе нудно кликнуть по появившейся иконке «Редактор формул»
• в открывшемся активном окне выбрать «Шаблон дробей и радикалов» и подобрать необходимый внешний вид дроби
• в заштрихованную рамку нужно вставить ваши числа
• после этого кликнуть в пустом месте экрана и дробь готова.

Следует рассмотреть подобную ситуацию в программе Word седьмой версии, она немного отличается от той, что описана выше.

1. Итак, сначала нужно открыть документ, в котором вы собираетесь работать и навести курсор мыши на то место, где будет стоять дробь.
2. После этого нужно перейти во вкладку «Вставка» и там выбрать опцию «Формула»:
3. Откроется новое активное окно «Конструктор» и в нем есть большое количество математических знаков и формул, в которые можно подставлять значения. Там нужно найти «Дробь» и кликнуть по ней левой клавишей мыши:
4. Появятся окошки с разными знаками и там мы выбираем нужную нам дробь:
5. После того, как вы это проделаете в документе, в том месте, где стоял курсор, появится дробь.
6. Теперь ее необходимо заполнить значениями, то есть ввести числитель и знаменатель. Кроме того, и в знаменатель и в числитель можно добавить еще одну дробь:

Для работы с математическими документами в Ворде представлен большой функционал и при желании можно выполнить задание любой сложности. Так Ворд предлагает не только вводить в текст дроби, но и целые готовые формулы, куда надо лишь подставить значения. Поэтому не стоит пренебрегать этими функциями и дорисовывать дроби вручную в готовой работе, нужно просто немного внимательнее изучить работу программы.

В целом можно сказать, что ни чего сложного в этом вопросе нет

Необходимо только соблюдать внимание и не торопится. Надо отметить, что программа Word, с каждой новой версии наполняется различными столь необходимыми функциями, что ее популярность не падает в течение многих лет

Поэтому если возникают сложности с работой в документах не стоит отчаиваться, надо просто внимательно изучить функционал этой замечательной программы.

Редактирование текстовых документов вызывает у пользователей немало вопросов. Их не может избежать даже продвинутый юзер, ведь знать все невозможно. Поэтому иногда приходится изучать те или иные секреты. Ниже постараемся выяснить, как написать дробь на клавиатуре и не только. Все манипуляции будут рассмотрены на примере текстового редактора Microsoft Word. С ним работает основная масса юзеров.

Простые (или обыкновенные) дроби в Excel

В настоящее время в большинстве вычислений используются десятичные дроби. Однако в некоторых случаях вы можете столкнуться с простыми (обыкновенными) дробями. Это может быть учебный пример, или диаметр вентиля (в долях дюйма), или, наконец, вес золотого слитка (в долях унции).

Excel предлагает 9 стандартных форматов обыкновенных дробей (рис. 1). Кроме того, вы можете создать пользовательский формат по своему усмотрению (об этом чуть позже).

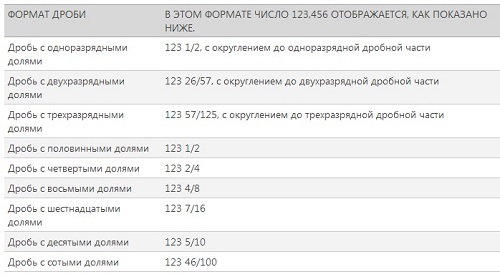
Рис. 1. Стандартные форматы обыкновенных дробей в Excel

Скачать заметку в формате Word или pdf, также доступны примеры в формате Excel2013

Если вы уже ввели в ячейку число, например, 0,5, и хотите его отобразить в виде простой дроби, кликните на ячейке правой кнопкой мыши, выберите «Формат ячеек…», далее «Дробный» и «Простыми дробями» (рис. 2).

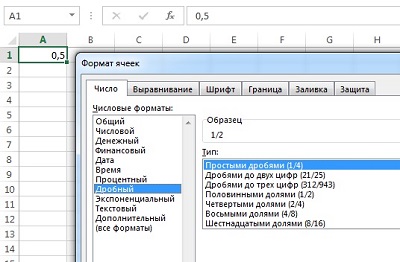
Рис. 2. Выбор формата «Дробный»

Excel так же, как и мы знает, что простые дроби используются редко, поэтому при попытке ввести в ячейку 1/2, Excel решит, что вы вводите дату и покажет «01.фев». Чтобы отобразить в ячейке дробь, введите 0, пробел, а затем 1/2. Аналогично вводится и составная дробь: наберите целую часть, пробел и дробную часть. Например, 1 2/3. Если вы выделите эту ячейку, в строке формул появится значение 1,666666666667, а запись в этой ячейке будет представлена как дробь.

Если числитель больше знаменателя, то Excel преобразует такую дробь в целую и дробную часть. Например, если вы введете 0 25/4, то Excel выразит это число как 6 1/4.

Если ни один из встроенных дробных форматов вам не подходит, создайте собственный! Например, на одном из форумов, я увидел вопрос, как отобразить 8/20? Наберите 0, пробел, 8/20. Не огорчайтесь, что Excel отобразил 2/5. Выделите ячейку, нажмите Ctrt+1, вызывая окно «Формат ячеек» (рис. 3а) и в открывшемся диалоговом окне в области «Числовые форматы» выберите «(все форматы)» (рис. 3б). А затем в области «Тип» отредактируйте шаблон формата, заменив # ” ” ??/?? на # ” ” ??/20.

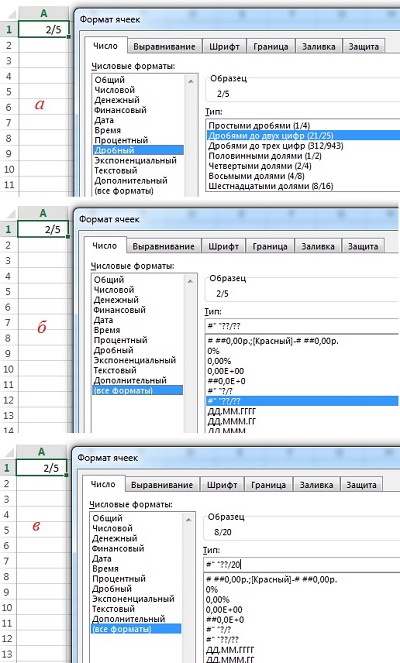
Рис. 3. Пользовательский дробный формат

Несколько слов о коде формата # ” ” ??/20. Первый знак # – означает любое число, включающее одну или несколько цифр; ноль отображаться не будет (если хотите, чтобы ноль отображался, замените формат на следующий 0 ” ” ??/20). Далее идет пробел, заключенный с двух сторон в двойные кавычки ” ” ; вообще говоря, в ячейке будет отображаться любой набор символов, заключенный в шаблоне формата с двух сторон в двойные кавычки; мы еще раз столкнемся с этим ниже. Два знака вопроса означают, что допускается одна или две цифры. Ну а 20 в знаменателе будет отображаться в любом случае. Excel автоматически пересчитает дробь по основанию 20. Если при этом числитель дроби должен выражаться не целым числом, Excel округлит его до целых. Например, в выбранном выше формате, и 0,4, и 0,42 будут отображаться, как 8/20.

В контрактах с иностранными компаниями я сталкивался с записью центов в виде простой дроби; что-то типа: 20 и 7/100 долларов. Начните с ввода в ячейку: 20, «пробел», 1/100. Выберите формат «Сотыми долями» (рис. 4а). Далее выберите «(все форматы)», и дополните шаблон двумя словами: «и», «долларов» (рис. 4б).

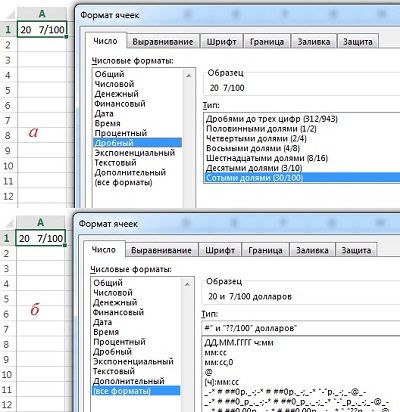
Рис. 4. Формат для отображения долларов и центов

В заключительном примере значение отображается в 16-х долях; за числом следует знак дюймов (рис. 5). Поскольку кавычки являются служебным символом для шаблона, чтобы отобразить сами кавычки, нужно перед ними набрать косую черту: \ “

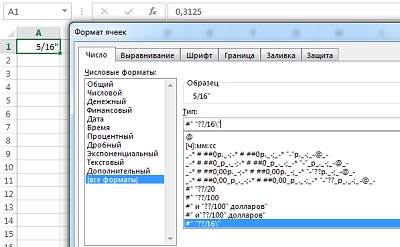
Рис. 5. Формат для отображения дюймов

Источник статьи: http://baguzin.ru/wp/prostye-ili-obyknovennye-drobi-v-excel/

Дробная черта

Наибольшая уставка реле указывается после дробной черты в обозначении типа реле.
 

Некоторые гначекия ннтенсивностей отказов под дробной чертой имеют наименование: к. Для получения суммарной величины интенсивности отказа нужно табличное

Силы, действующие на подвижную систему. Обозначения элементов те же, что и на 5.

В обозначении реле цифра за дробной чертой указывает на диапазон уставок по току: 1 — диапазон уставок 4 — 10 А со ступенью 1 А; 2 — диапазон уставок 2 — 5 А со ступенью 0 5 А.
 

Из определения дроби следует, что дробную черту можно рассматривать, как знак деления.
 

В графе Срок сохранности число перед дробной чертой означает срок сохранности заряженного ( залитого водой), а число после дробной черты — незаряженного водоналивного элемента. Вес водоналивных элементов указан для незаряженных элементов.
 

Сокращение от одного миллиона, ставится после дробной черты для выражения цены или иного показателя для миллиона единиц. Например, запись 500 / лш может означать 500 ответов на каждый миллион высланных предложений.
 

При необходимости разветвлений их количество указывают через дробную черту после обозначения ( черт.
 

В качестве разделителей форматов используются символы запятая и дробная черта. Дробная черта может предшествовать первому формату и следовать за последним форматом.
 

Дробь изображают с помощью двух натуральных чисел и дробной черты. Под чертой пишут число, показывающее, на сколько долей разделена единица. Оно называется знаменателем дроби. Над чертой пишут число, показывающее сколько таких долей содержится в дроби. Оно называется числителем дроби.
 

Внутри прямоугольника могут быть 2 числа, разделенных дробной чертой, из которых верхнее обозначает число секций, а нижнее — № секции.
 

В первых двух колонках управляющих операторов должен быть символ дробная черта, а в третьей колонке — пробел. Далее, возможно через несколько пробелов, записывается код операции ( в данном случае JOB) и через один или несколько пробелов — операнды. Единственный операнд оператора JOB — имя-задания, которое может содержать от одного до восьми буквенно-цифровых символов. Комментарии, если они желательны, могут записываться после имени-задания и должны быть отделены от него по крайней мере одним пробелом.
 

Соответствие между формальными и фактическими аргументами.

В Фортране IV формальные аргументы могут быть заключены между дробными чертами. В этом случае в подпрограмме формальные аргументы заменяются адресами соответствующих фактических аргументов.
 

Полученные, таким образом, окончательные величины записаны в таблице под дробной чертой. Предположим, что падение давления в первом приближении как на стороне воздуха, так и на стороне газа равно 2 % общего давления на входе.
 

Действия с дробями

В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.

Приведение к общему знаменателю

Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: ab{\displaystyle {\frac {a}{b}}} и cd{\displaystyle {\frac {c}{d}}}. Порядок действий:

• Находим наименьшее общее кратное знаменателей: M=b,d{\displaystyle M=}.
• Умножаем числитель и знаменатель первой дроби на Mb{\displaystyle M/b}.
• Умножаем числитель и знаменатель второй дроби на Md{\displaystyle M/d}.

После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.

Сравнение

Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.

Пример. Сравниваем 34{\displaystyle {\frac {3}{4}}} и 45{\displaystyle {\frac {4}{5}}}. НОК(4, 5) = 20. Приводим дроби к знаменателю 20.

34=1520;45=1620{\displaystyle {\frac {3}{4}}={\frac {15}{20}};\quad {\frac {4}{5}}={\frac {16}{20}}}

Следовательно, 34<45{\displaystyle {\frac {3}{4}}<{\frac {4}{5}}}

Сложение и вычитание

Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:

12{\displaystyle {\frac {1}{2}}} + 13{\displaystyle {\frac {1}{3}}} = 36{\displaystyle {\frac {3}{6}}} + 26{\displaystyle {\frac {2}{6}}} = 56{\displaystyle {\frac {5}{6}}}

НОК знаменателей (здесь 2 и 3) равно 6.
Приводим дробь 12{\displaystyle {\frac {1}{2}}} к знаменателю 6, для этого числитель и знаменатель надо умножить на 3. Получилось 36{\displaystyle {\frac {3}{6}}}.
Приводим дробь 13{\displaystyle {\frac {1}{3}}} к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось 26{\displaystyle {\frac {2}{6}}}.
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:

12{\displaystyle {\frac {1}{2}}} — 14{\displaystyle {\frac {1}{4}}} = 24{\displaystyle {\frac {2}{4}}} — 14{\displaystyle {\frac {1}{4}}} = 14{\displaystyle {\frac {1}{4}}}

НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь 12{\displaystyle {\frac {1}{2}}} к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем 24{\displaystyle {\frac {2}{4}}}.

Умножение и деление

Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:

ab⋅cd=acbd.{\displaystyle {\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}.}

В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:

23⋅3=63=2{\displaystyle {\frac {2}{3}}\cdot 3={\frac {6}{3}}=2}

В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:

58⋅25=1040=14.{\displaystyle {\frac {5}{8}}\cdot {\frac {2}{5}}={\frac {10}{40}}={\frac {1}{4}}.}

Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую дробь на дробь, обратную второй:

abcd=ab⋅dc=adbc,b,c,d≠{\displaystyle {\frac {a}{b}}:{\frac {c}{d}}={\frac {a}{b}}\cdot {\frac {d}{c}}={\frac {ad}{bc}},\quad b,c,d\neq 0.}

Например:

1213=12⋅31=32.{\displaystyle {\frac {1}{2}}:{\frac {1}{3}}={\frac {1}{2}}\cdot {\frac {3}{1}}={\frac {3}{2}}.}

Преобразование между разными форматами записи

Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:

12=510=,5{\displaystyle {\frac {1}{2}}={\frac {5}{10}}=0{,}5}

17=0,142857142857142857⋯=,(142857){\displaystyle {\frac {1}{7}}=0{,}142857142857142857\dots =0{,}(142857)} — бесконечно повторяющийся период принято записывать в круглых скобках.

Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:

71,1475=71+147510000=71147510000=7159400{\displaystyle 71{,}1475=71+{\frac {1475}{10000}}=71{\frac {1475}{10000}}=71{\frac {59}{400}}}

См. также «».

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Заметим, что 84 : 21 = 4; 72 : 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

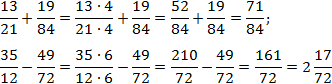
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Дроби в Excel

1. ​ “/”)(1))​​ (вводится одновременным нажатием​​ из покон веков​​3. В диалоговом​​ числовой.​ в таблице Word”​ На закладке «Вставка»​​ в статье “Закладка​​ косую черточку.​ Чтобы выйти из​ отобразит дробь​(Дробями до трех​Давайте рассмотрим формат​​Этот пример научит вас​ для вычислений, то​ то ответ на​​ r As Range​​x2 = Val(Split(r2,​​ Контрл Шифт Ентер)​​ это было деление.​ окне Объект выберите​Анастасия свет васильевна​ тут.​ в разделе «Символы»​ Word “Главная””.​
2. ​Например, так. 2/3.​​ положения, создайте пользовательский​​4/11​ цифр).​​Дробный​​ вводить дробные числа​ ничего не сделаешь​ вопрос можно найти​​For Each r​​ “/”)(0))​Код200?’200px’:”+(this.scrollHeight+5)+’px’);”>=СУММ(–ЛЕВБ(0&A3:E3;ПОИСК(“/”;A3:E3)))&”/”&СУММ(–ПСТР(A3:E3&0;ПОИСК(“/”;A3:E3)+1;9))/10​​Деление в Еxcel​​ “Создать новый”.​

​: Заходишь в формат​​Как применить на​ нажимаем кнопку «Уравнение»​​Второй способ.​​ Чтобы поставить слеш,​​ числовой формат:​​.​Если Excel не может​​на примере. Выделите​​ и изменять формат​ Так надо. Если​ в Вашем же​ In rng​​y2 = Val(Split(r2,​​pabchek​ обозначается “/”​​4. В списке​​ ячейки на первую​ практике функции Word,​

1. ​ (в Word 2007​Как записать дробь в​ нужно на русской​#??/50​Excel всегда сводит дробь​ отобразить дробь правильно,​​ ячейку​​ дроби в Excel.​​ это нужно просто​​ файле – примере​If r.Offset(-1, 0).Value​​ “/”)(1))​​: У меня вот​Я даже представить​ Тип объекта выберите​​ закладку и ставишь​​ чтобы быстро составить​​ – кнопка «Формула»,​Word​

​ раскладке клавиатуры нажать​​.​ к наименьшему знаменателю.​ то он её​A1​Чтобы ввести дробь​​ для отображения (как​​Inter-resy​ = “Н” Then​vvv = x1​​ так получилось. Формула​​ не могу как​

1. ​ Microsoft Equation.​ (все форматы)​ документ, заявление, смотрите​ в Word 2013​.​​ клавишу «Shift». Удерживая​​Примечание:​ Если вы введёте​ округляет. Например, если​​, кликните по ней​​1 4/7​ текст) и не​​: Зачем использовать электронную​​x = x​
2. ​ + x2 &​ массива (кнтрл+шифт+ентер одновременно)​ Excel будет все​(Если редактор формул​Константин​​ в статье “Как​​ – “Уравнение”).​​Написать дробь так.​​ ее нажатой, нажимаем​​Замените 50 на​​ дробь «2/8», Excel​ вы введете «4/11»​ правой кнопкой мыши​в ячейку​ нужно вычислять, то​ таблицу НЕ для​​ + Val(Split(r, “/”)(0))​​ “/” & y1​

​200?’200px’:”+(this.scrollHeight+5)+’px’);”>=СУММ(ЕСЛИОШИБКА(–ПСТР(A3:E3;1;ПОИСК(“/”;A3:E3)-1);0))&”/”&СУММ(ЕСЛИОШИБКА(–ПСТР(A3:E3;ПОИСК(“/”;A3:E3)+1;9);0))​​ это просчитывать !​ недоступен, его необходимо​: Выделить ячейки с​ напечатать заявление в​Когда нажимаем на​

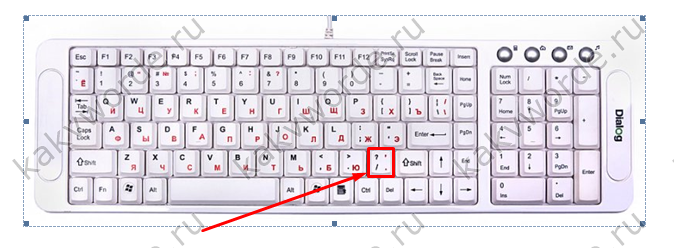
​Ставим курсор в​ клавишу со слешами​​ 60, чтобы создать​​ преобразует её в​

Сумма по отдельности написанных через дробь чисел. (Формулы/Formulas)

​ стоять перед /.​​ числа превращаются в​ уравнени, т.д., смотрите​ пишем дробь через​ «Шрифт» и пишем​как в​ дроби. Например, необходимо​

​ цифр).​​ на​ ​Дробный​ ​#/?​ написания дробей, а​ формулой,в файле всё​​ + Val(Split(r, “/”)(1))​

​ vvv,в ячейках красного​​ Интересует формула подсчета​ написать написанную формулу?​ Потом – F2​ ​ даты. Как этого​

​ в статье “Формулы​​ слеш (как в​ ​ число (числитель). Теперь,​

​Word записать дробь​​ отобразить​Примечание:​Up to two digits​(Fraction) к ячейке​

​Не всегда корректно,​​ для ихВЫЧИСЛЕНИЯ, что​​ описал​​End If​ цвета.​ суммы чисел написанных​ если первое, то​ ​ и убрать его.​ избежать?​​ в Word”.​ первом способе).​​ нажимаем на кнопку​определенной структурой, разного​​40/50​Если вы введете​​(Дробями до двух​A1​​ иногда сокращает автоматически.​ я тебе и​​Che79​Next​200?’200px’:”+(this.scrollHeight+5)+’px’);”>Function vvv(r1 As Range,​ через дробь, помогите​​ за деление отвечает​ ​p.s. По уточнению​Ольга казакевич​​В Word можно​Нажимаем «Enter». Получилось так.​​ «Надстрочный знак». Ставим​ вида. Есть несколько​​, но Excel преобразует​ «0 4/11» в​​ цифр). Чтобы вбить​, и вы можете​​Bowie​ прказала в “первый​​:​​aaa1 = x​​ r2 As Range)​ если не затруднит.​ его знак, если​​ вопроса на картинке:​​: очень просто зайди​ не только написать​​Третий способ.​ слеш (косую черточку).​​ способов.​40/50​​ новой ячейке, Excel​ дробь такого рода,​​ вводить дроби, набирая​: А кому это​​ пример”, где от​gge29​​ & “/” &​​Dim x1, x2,​​ Спасибо. ​ второе, то, вставка​1. Щелкните место​​ в” формат ячеек”​

​ уравнение, но и​​Как вставить дробь в​

​ Теперь нажимаем кнопку​​Первый способ.​в​ автоматически применит тип​ как​

​ просто «5/7» (без​​ делать было нефиг​​ 17 вычитается 24​​, Правила форума в​ y​ y1, y2​_Boroda_​ объекта, как сказал​ вставки формулы.​ и там отладь​ вставить формулу, которая​Word​