Возведение в степень
Содержание:
- Возведение в степень (**)
- Менеджеры контекста
- Дополнение 1: Как вызывать магические методы
- Приоритет
- Вспомогательные методы
- Функции из библиотеки Math
- Способы извлечения корня
- Операции с числами
- Модуль Decimal
- 5 функций для отладки
- Экспоненциальные и логарифмические функции
- Арифметические операции с целыми и вещественными числами
- Как посчитать сумму введенных чисел?
- Различие округления в Python 2 и Python 3
- Деление на ноль
- История
- Системы счисления
- Best Practices
- Деление без остатка
- Встроенные функции
- Арифметические операции
- Комплексные числа в Python (complex)
- Арифметические операции
- Комплексные числа (complex)
- Операторы присваивания
- Вывод
Возведение в степень (**)
Нетипичный оператор для большинства других языков программирования. Тем он и удобен. Парная «звёздочка» (**) выполняет классическое математическое возведение числа «a» в степень «b»:
И показатель степени, и основание могут быть отрицательными:
И дробными:
Операндов у возведения в степень также может быть несколько. В таком случае, оператор «**» работает, как право-ассоциативный (т.е. операции выполняются справа-налево):
В завершении — про приоритет операций. Если в выражении используются разные операторы, то порядок их выполнения будет следующим:
- возведение в степень;
- умножение, деление, целочисленное деление и деление по модулю;
- сложение и вычитание.
Менеджеры контекста
PEP 343
-
Определяет, что должен сделать менеджер контекста в начале блока, созданного оператором . Заметьте, что возвращаемое значение и есть то значение, с которым производится работа внутри .
-
Определяет действия менеджера контекста после того, как блок будет выполнен (или прерван во время работы). Может использоваться для контроллирования исключений, чистки, любых действий которые должны быть выполнены незамедлительно после блока внутри with. Если блок выполнен успешно, , , и будут установлены в . В другом случае вы сами выбираете, перехватывать ли исключение или предоставить это пользователю; если вы решили перехватить исключение, убедитесь, что возвращает после того как всё сказано и сделано. Если вы не хотите, чтобы исключение было перехвачено менеджером контекста, просто позвольте ему случиться.
contextlib
Дополнение 1: Как вызывать магические методы
| Магический метод | Когда он вызывается (пример) | Объяснение |
|---|---|---|
| вызывается при создании экземпляра | ||
| вызывается при создании экземпляра | ||
| , , etc. | Вызывается для любого сравнения | |
| Унарный знак плюса | ||
| Унарный знак минуса | ||
| Побитовая инверсия | ||
| Преобразование, когда объект используется как индекс | ||
| , | Булевое значение объекта | |
| Пытаются получить несуществующий атрибут | ||
| Присвоение любому атрибуту | ||
| Удаление атрибута | ||
| Получить любой атрибут | ||
| Получение элемента через индекс | ||
| Присвоение элементу через индекс | ||
| Удаление элемента через индекс | ||
| Итерация | ||
| , | Проверка принадлежности с помощью | |
| «Вызов» экземпляра | ||
| оператор менеджеров контекста | ||
| оператор менеджеров контекста | ||
| Сериализация | ||
| Сериализация |
Приоритет
Иногда выражение содержит несколько операторов. В этом случае приоритет оператора используется для определения порядка выполнения.
- Мы можем создать группу выражений, используя круглые скобки. Выражение в скобках сначала вычисляется, прежде чем они смогут участвовать в дальнейших вычислениях.
- Некоторые операторы имеют одинаковый уровень приоритета. В этом случае выражение оценивается слева направо.
В таблице ниже перечислены приоритеты операторов в порядке убывания.
| Приоритет |
|---|
| ** (экспонента) |
| ~ (Дополнение к единицам) |
| *, /, //, % (Умножение, Деление, Операторы Модуля) |
| +, – (Сложение, Вычитание) |
| <<, >> (операторы сдвига вправо и влево) |
| & (побитовый AND) |
| |, ^ (побитовый OR, XOR) |
| ==, !=, >, <, >=, <= (сравнения) |
| =, +=, -=, *=, /=, //=, %= (присваивания) |
| is, is not (идентификации) |
| in, not in (принадлежности) |
| not, and, or (логические) |
Вспомогательные методы
К ним относят:
• float.as_integer_ratio() — это пара целых чисел int, отношение которых равно этому числу;
• float.is_integer() — функция определят, является ли данное значение целым числом;
• float.hex() — функция переводит float в 16-тиричную систему счисления, то есть в hex;
• classmethod float.fromhex(s) — функцию используют для получения float из 16-тиричной строки.
Кроме стандартных выражений, в Python есть и специальные полезные модули. Например, модуль math позволяет выполнять более сложные арифметические функции:
>>> >>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
А вот модуль random запускает генератор случайных чисел, позволяя реализовать функции случайного выбора:
>>> >>> import random >>> random.random() 0.75849839767373282
Функции из библиотеки Math
Модуль необходим в Python. Он предоставляет пользователю широкий функционал работы с числами. Для обработки алгоритмов сначала проводят импорт модуля.
math.ceil
Функция преобразовывает значение в большую сторону (вверх). Этот термин применяется и в математике. Он означает число, которое равно или больше заданного.
Любая дробь находится между двумя целыми числами. Например, 2.3 лежит между 2 и 3. Функция ceil() определяет большую сторону и возводит к нему результат преобразования. Например:
Алгоритм определяет большую границу интервала с учетом знака:
math.floor
действует противоположно – округляет дробное значение до ближайшего целого, которое меньше или равно исходному. Округление происходит в меньшую сторону (вниз):
При округлении учитывается знак перед данными.
math.trunc
Функция характеризуется отбрасыванием дробной части. После преобразования получается целое значение без учета дроби. Такой алгоритм не является округлением в арифметическом смысле. В Пайтон просто игнорируется дробь независимо от ее значения:
Избавиться от дроби можно без подключения модуля. Для этого есть стандартная функция Она преобразовывает дробные числа в целые путем игнорирования дроби.
Способы извлечения корня
В языке программирования Python 3 существует три способа извлечения корней:
- Использование функции sqrt из стандартной математической библиотеки math.
- Операция возведения в степень **
- Применение функции pow(x, n)
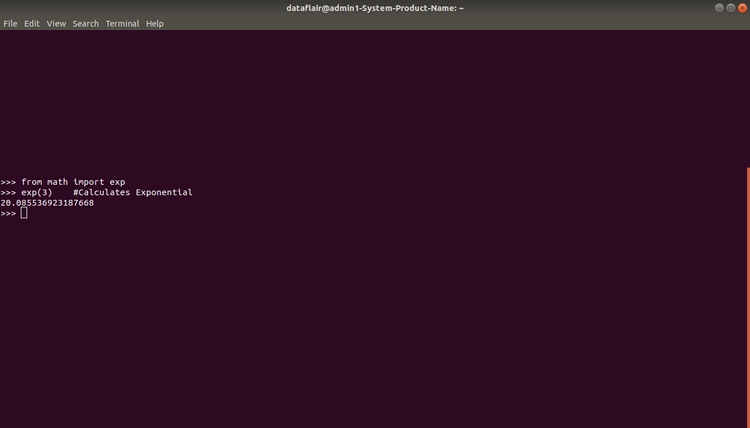
Чтобы воспользоваться первым способом, необходимо вначале импортировать sqrt из модуля math. Это делается с помощью ключевого слова import: . При помощи этой функции можно извлекать только квадратный корень из числа. Приведем пример:
from math import sqrt x = sqrt(4) print(x) 2.0
Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.
from math import hypot x = hypot(4,3) print(x) 5.0
Еще одним, чуть более универсальным методом, будет использование возведения в степень. Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:
n = 2 x = 4**(1./n) print(x) 2.0
Обратите внимание, что в Python 2 необходимо ставить точку после единицы, иначе произойдет целочисленное деление, и 1/n == 0, а не нужной нам дроби. В Python 3 можно не ставить точку.. Последний метод использует функцию pow(value, n)
Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа
Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.
x = pow(4, 0.5) print(x) 2.0
Какой метод быстрее?
Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.
from time import monotonic
from math import sqrt
iterations = 1000000
start = monotonic()
for a in range(iterations):
x = sqrt(4)
print("sqrt time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")
sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds
Как видно, самое быстрое решение – использовать **. На втором месте метод sqrt, а pow – самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.
Таким образом, если критична скорость, то используем **. Если скорость не критична, а важна читаемость кода, то следует использовать sqrt.
Операции с числами
Является ли переменная числом
Любую переменную можно проверить на тип (int, float или complex):
Если вы хотите проверить, находится ли в строке число, воспользуйтесь методом
Однако стоит помнить, что метод не работает для отрицательных чисел и чисел с плавающей точкой.
Также для проверки на число, можно написать собственную функцию:
Арифметические операции
- – сложение;
- – вычитание;
- – умножение;
- – деление;
- – целочисленное деление;
- – остаток от деления;
- – возведение в степень;
- – смена знака;
- – модуль числа;
- – возвращает кортеж из частного и остатка от деления x на y;
- – возведение числа в степень (z – деление по модулю);
- – округление числа (ndigits — знаки после запятой).
Преобразования
- – преобразование в целое число
- – преобразование в число с плавающей точкой
- – преобразование в комплексное число
- – целоe числа в двоичную строку;
- – целое число в восьмеричную строку;
- – целое число в шестнадцатеричную строку;
- – перевод целого числа 123 в список цифр этого числа;
- – перевод списка цифр в целое число 123;
- – число в строку;
Ввод чисел
Для ввода данных в программу на языке Python используется функция . Эта функция считывает то что вы ввели на клавиатуре, и записывает эти данные в переменную в виде одной строки. После этого, перевести строку в число можно простыми функциями , или
Если нужен список чисел, введите несколько чисел через пробел и выполните:
Вывод чисел
Для вывода числа используйте
На практике возникают ситуации, когда нужно вывести число вместе со строкой (например пояснить, что означает число). Существует несколько вариантов сделать это:
Другие полезные функции
- – посчитает длину числа;
- – если остаток от деления равен 0, то число четное;
- – диапазон чисел от 0 до 5, по которому можно итерироваться;
- – перевернет число (123 -> 321).
Модуль Decimal
Синтаксис
Decimal обеспечивает поддержку правильного округления десятичной арифметики с плавающей точкой.
, в отличие от , имеет ряд преимуществ:
- работает так же, как школьная арифметика;
- десятичные числа представлены точно (в отличие от float, где такие числа как 1.1 и 5.12 не имеют точного представления);
- точность десятичного модуля Decimal можно изменять (с помощью );
Точность
Контекстом в Deciaml можно управлять, устанавливая свои значения. Например, для того, чтобы управлять точностью Decimal, необходимо изменить параметр контекста (от англ. precision – точность):
Округление
Округление осуществляется с помощью метода . В качестве первого аргумента – объект Decimal, указывающий на формат округления:
Важно: если точность округления установлена в , а формат округления , возникнет ошибка:
Чтобы избежать ее, необходимо поменять точность округления, как было сделано в примере выше:
Помимо первого параметра, quantize() принимает в качестве второго параметра стратегию округления:
- – округление в направлении бесконечности (Infinity);
- – округляет в направлении минус бесконечности (- Infinity);
- – округление в направлении нуля;
- – округление до ближайшего четного числа. Число 4.9 округлится не до 5, а до 4 (потому что 5 – не четное);
- – округление до ближайшего нуля;
- – округление от нуля;
- – округление от нуля (если последняя цифра после округления до нуля была бы 0 или 5, в противном случае к нулю).
Помните, что как округление, так и точность вступают в игру только во время арифметических операций, а не при создании самих десятичных дробей
5 функций для отладки
Эти функции часто игнорируются, но будут полезны для отладки и устранения неисправностей кода.
breakpoint
Если нужно приостановить выполнение кода и перейти в командную строку Python, эта функция вам пригодится. Вызов перебросит вас в отладчик Python.
Эта встроенная функция была добавлена в Python 3.7, но если вы работаете в более старых версиях, можете получить тот же результат с помощью .
dir
Эта функция может использоваться в двух случаях:
- просмотр списка всех локальных переменных;
- просмотр списка всех атрибутов конкретного объекта.
Из примера можно увидеть локальные переменные сразу после запуска и после создания новой переменной .
Если в передать созданный список , на выходе можно увидеть все его атрибуты.
В выведенном списке атрибутов можно увидеть его типичные методы (, , и т. д.) , а также множество более сложных методов для перегрузки операторов.
vars
Эта функция является своего рода смесью двух похожих инструментов: и .
Когда вызывается без аргументов, это эквивалентно вызову , которая показывает словарь всех локальных переменных и их значений.
Когда вызов происходит с аргументом, получает доступ к атрибуту , который представляет собой словарь всех атрибутов экземпляра.
Перед использованием было бы неплохо сначала обратиться к .
type
Эта функция возвращает тип объекта, который вы ей передаете.
Тип экземпляра класса есть сам класс.
Тип класса — это его метакласс, обычно это .
Атрибут даёт тот же результат, что и функция , но рекомендуется использовать второй вариант.
Функция , кроме отладки, иногда полезна и в реальном коде (особенно в объектно-ориентированном программировании с наследованием и пользовательскими строковыми представлениями).
Обратите внимание, что при проверке типов обычно вместо используется функция. Также стоит понимать, что в Python обычно не принято проверять типы объектов (вместо этого практикуется утиная типизация)
help
Если вы находитесь в Python Shell или делаете отладку кода с использованием , и хотите знать, как работает определённый объект, метод или атрибут, функция поможет вам.
В действительности вы, скорее всего, будете обращаться за помощью к поисковой системе. Но если вы уже находитесь в Python Shell, вызов будет быстрее, чем поиск документации в Google.
Экспоненциальные и логарифмические функции
import cmath
a = 3 + 4j
print('e^c =', cmath.exp(a))
print('log2(c) =', cmath.log(a, 2))
print('log10(c) =', cmath.log10(a))
print('sqrt(c) =', cmath.sqrt(a))
Вывод:
e^c = (-13.128783081462158-15.200784463067954j) log2(c) = (2.321928094887362+1.3378042124509761j) log10(c) = (0.6989700043360187+0.4027191962733731j) sqrt(c) = (2+1j)
Другие
Есть несколько разных функций, чтобы проверить, является ли комплексное число конечным, бесконечным или . Также есть функция проверки близости двух комплексных чисел.
>>> print(cmath.isfinite(2 + 2j)) True >>> print(cmath.isfinite(cmath.inf + 2j)) False >>> print(cmath.isinf(2 + 2j)) False >>> print(cmath.isinf(cmath.inf + 2j)) True >>> print(cmath.isinf(cmath.nan + 2j)) False >>> print(cmath.isnan(2 + 2j)) False >>> print(cmath.isnan(cmath.inf + 2j)) False >>> print(cmath.isnan(cmath.nan + 2j)) True >>> print(cmath.isclose(2+2j, 2.01+1.9j, rel_tol=0.05)) True >>> print(cmath.isclose(2+2j, 2.01+1.9j, abs_tol=0.005)) False
Арифметические операции с целыми и вещественными числами
Все эксперименты будем производить в Python, запущенном в интерактивном режиме.
Сложение.
Складывать можно непосредственно сами числа…
>>> 3+2 5
либо переменные, но они должны предварительно быть проинициализированы.
>>> a = 3 >>> b = 2 >>> a + b 5
Результат операции сложения можно присвоить другой переменной…
>>> a = 3 >>> b = 2 >>> c = a + b >>> print(c) 5
либо ей же самой, в таком случае можно использовать полную или сокращенную запись, полная выглядит так
>>> a = 3 >>> b = 2 >>> a = a + b >>> print(a) 5
сокращенная так
>>> a = 3 >>> b = 2 >>> a += b >>> print(a) 5
Все перечисленные выше варианты использования операции сложения могут быть применены для всех нижеследующих операций.
Вычитание.
>>> 4-2 2 >>> a = 5 >>> b = 7 >>> a - b -2
Умножение.
>>> 5 * 8 40 >>> a = 4 >>> a *= 10 >>> print(a) 40
Деление.
>>> 9 3 3. >>> a = 7 >>> b = 4 >>> a b 1.75
Получение целой части от деления.
>>> 9 3 3 >>> a = 7 >>> b = 4 >>> a b 1
Получение остатка от деления.
>>> 9 % 5 4 >>> a = 7 >>> b = 4 >>> a % b 3
Возведение в степень.
>>> 5 ** 4 625 >>> a = 4 >>> b = 3 >>> a ** b 64
Как посчитать сумму введенных чисел?
В команде input() можно передавать подсказки.
w = int(input(«Введите первое число: «)) q = int(input(«Введите второе число: «)) summa=w+q print(summa)
Введите первое число: 6 Введите второе число: 7 13
Копирование материалов разрешается только с указанием автора (Михаил Русаков) и индексируемой прямой ссылкой на сайт (http://myrusakov.ru)!
Добавляйтесь ко мне в друзья : http://vk.com/myrusakov.Если Вы хотите дать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.
Если Вы не хотите пропустить новые материалы на сайте,то Вы можете подписаться на обновления: Подписаться на обновления
Если у Вас остались какие-либо вопросы, либо у Вас есть желание высказаться по поводу этой статьи, то Вы можете оставить свой комментарий внизу страницы.
Порекомендуйте эту статью друзьям:
Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):
Она выглядит вот так:
BB-код ссылки для форумов (например, можете поставить её в подписи):
Различие округления в Python 2 и Python 3
В Python 2 и Python 3 реализованы разные принципы округления.
В Python 2 используется арифметическое округление. В нем наблюдается большое количество погрешностей, что приводит к неточностям в процессе вычислений.
Во втором Python есть только 4 цифры, которые ведут к преобразованию к меньшему значению – 1, 2, 3 и 4. Также 5 цифр, которые приводят к большему значению – 5, 6, 7, 8, 9. Такое неравное распределение ведет к тому, что погрешность постоянно нарастает.
Python 2 по правилам арифметического округления преобразует число 5,685 в 5,68 до второго знака. Такая погрешность связана с тем, что десятичные цифры float в двоичном коде невозможно корректно представить.
В Python 3 используются принципы банковского округления. Это означает, что преобразование производится к ближайшему четному. В таком случае также не удается полностью избежать возникающих ошибок, но программисты добиваются точности в подсчетах.
2,5 по правилам банковского преобразования будет равно 2, а 3,5 = 4 (значения возводятся к близкому четному). Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.
Деление на ноль
Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.
Исключение следует обрабатывать, это можно сделать так:
try:
print(24 / 0)
except Exception as e:
print(e)
division by zero
Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить на .
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:
a = 14
b = None
if a == 0:
print('делитель равен нулю!')
else:
b = 345/a
print('Операция выполнена, результат = ' + str(b))
Операция выполнена, результат = 24.642857142857142
История
Возведение в степень – частный случай умножения, поэтому данную операцию изначально не рассматривали, как самостоятельную. Но уже в работах Диофанта Александрийского степени отведено особое место. В частности «Отец Алгебры» применял понятия кубов и квадратов числа.
Эта операция была известна ещё в древнем Вавилоне, однако современный её вид устоялся лишь в XVII веке.
Как умножение позволяет сократить количество символов сложения:
Так и степень сокращает запись умножения:
- 6 – это основание;
- 2 – показатель степени (это число говорит о том, сколько раз число в основании должно быть умножено само на себя).
До воцарения числового показателя, были и другие варианты его записи. Математики раннего Возрождения использовали буквы. Например, Q обозначала квадрат, а C – куб. Различные формы записи возведения в степень не обошли и языки программирования.
Системы счисления
Python поддерживает десятичные, двоичные, восьмеричные и шестнадцатеричные целые числа, причем не накладывается никаких ограничений на величину (длину) числа, лишь бы хватило памяти для его хранения.
Десятичные целые числа создаются, как обычно, с помощью десятичных цифр:
причем, в десятичной системе счисления ни одно число, кроме нуля не может начинаться с цифры \(0\), что в общем-то и ежу понятно, но это значит что отбрасывания незначащих нулей не происходит, а их наличие приводит к ошибке:
Двоичные числа состоят из префикса (или ) и двоичных цифр: \(0\) и \(1\):
Восьмеричные числа начинаются с префикса () и могут содержать только восьмиричные цифры: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\) и \(7\):
Шестнадцатеричные числа начинаются с префикса () и могут содержать как все десятичные цифры, так и символы латинского алфавита: (или ), которые в данном случае выступают в роли цифр:
В языках со строгой типизацией необходимо указывать как тип числа, так и то, что создаваемый объект сам является числом. Но в Python такой необходимости нет, интерпретатор сам, на основе анализа , способен понять что перед ним: число или нет, целое или вещественное, восьмеричное или двоичное.
Кстати, благодаря встроенной функции мы можем перевести в десятичную систему счисления, любое число представленное в другой системе счисления с основанием меньшим \(37\). Интересующее число указывается в виде строки в первом аргументе, а система счисления в котором оно представлено в виде целого числа во втором аргументе:
Best Practices
Последние абзацы статьи будут посвящены лучшим решениям практических задач, с которыми так или иначе сталкивается Python-разработчик.
Как перевести список в другой формат?
Иногда требуется перевести список в строку, в словарь или в JSON. Для этого нужно будет вывести список без скобок.
Перевод списка в строку осуществляется с помощью функции join(). На примере это выглядит так:
В данном случае в качестве разделителя используется запятая.
Словарь в Python – это такая же встроенная структура данных, наряду со списком. Преобразование списка в словарь — задача тоже несложная. Для этого потребуется воспользоваться функцией . Вот пример преобразования:
JSON – это JavaScript Object Notation. В Python находится встроенный модуль для кодирования и декодирования данных JSON. С применением метода можно запросто преобразовать список в строку JSON.
Как узнать индекс элемента в списке?
Узнать позицию элемента в последовательности списка бывает необходимым, когда элементов много, вручную их не сосчитать, и нужно обращение по индексу. Для того, чтобы узнать индекс элемента, используют функцию .
В качестве аргумента передаем значение, а на выходе получаем его индекс.
Как посчитать количество уникальных элементов в списке?
Самый простой способ – приведение списка к (множеству). После этого останутся только уникальные элементы, которые мы посчитаем функцией
Как создать список числовых элементов с шагом
Создание списка числовых элементов с шагом может понадобиться не так и часто, но мы рассмотрим пример построения такого списка.
Шагом называется переход от одного элемента к другому. Если шаг отрицательный, произойдёт реверс массива, то есть отсчёт пойдёт справа налево. Вот так выглядит список с шагом.
Еще один вариант – воспользоваться генератором списков:
При разработке на языке Python, списки встречаются довольно часто. Знание основ работы со списками поможет быстро и качественно писать программный код .
Деление без остатка
Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».
В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».
Примеры нахождения целой части от деления:
print(5 // 2) print(0 // 2) print(1234 // 5.0) 2 0 246.0
В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.
Встроенные функции
Для операции округления в Python есть встроенные функции – и
round
– округляет число (number) до ndigits знаков после запятой. Это стандартная функция, которая для выполнения не требует подключения модуля math.
По умолчанию операция проводится до нуля знаков – до ближайшего целого числа. Например:
Чтобы получить целый показатель, результат преобразовывают в .
Синтаксически функция вызывается двумя способами.
- – это округление числа до целого, которое расположено ближе всего. Если дробная часть равна 0,5, то округляют до ближайшего четного значения.
- – данные округляют до знаков после точки. Если округление проходит до сотых, то равен «2», если до тысячных – «3» и т.д.
int
– встроенная функция, не требующая подключения дополнительных модулей. Её функция – преобразование действительных значений к целому путем округления в сторону нуля. Например
Для положительных чисел функция аналогична функции , а для отрицательных – аналогично . Например:
Чтобы число по int преобразовать по математическим правилам, нужно выполнить следующие действия.
- Если число положительное, добавить к нему 0,5.
- Если число отрицательное, добавить -0,5.
Синтаксически преобразование оформляется так:
Арифметические операции
Целые числа поддерживают следующие математические операции, которые отсортированы по убыванию приоритета:
| № | Операция | Результат | Замечание |
|---|---|---|---|
| 1 | возводит x в степень y | (I) | |
| 2 | возводит x в степень y по модулю z, где z – необязательный аргумент | (I) | |
| 3 | возвращает кортеж с парой чисел | (II) | |
| 4 | возвращает \(\bar{x}\) — число, которое комплексно сопряжено с \(x\) | ||
| 5 | преобразует re в комплексное число (по умолчанию ) | (VI) | |
| 6 | преобразует x в вещественное число (число с плавающей точкой) | (VI) | |
| 7 | переобразует x в целое число, представленное в десятичной системе счисления | (V)(VI) | |
| 8 | абсолютное значение (модуль) числа x | ||
| 9 | делает число x положительным | ||
| 10 | делает число x отрицательным | ||
| 11 | остаток от деления x на y | (II) | |
| 12 | результат целочисленного деления x на y | (III) (II) | |
| 13 | результат «истинного» деления x на y | (IV) | |
| 14 | произведение x и y | ||
| 15 | разность x и y | ||
| 16 | сумма x и y |
Важно: приоритет математических операций выше побитовых логических операций и операций сравнения.
Замечания:
I. возведение \(0\) в степень \(0\) возвращает \(1\):
Извлечение корней четной степени из отрицательных чисел не вызывает ошибки, а возвращает комплексное число:
II. функция и операция , не работают для комплексных чисел. Для вас это может быть и очевидно, но не пользователя для которого вы пишите программу.
III. если оба числа типа int то и результат будет типа int. Данная операция всегда возвращает целое число, т.е. если число x можно представить в виде , то (r – остаток от деления). Так же следует иметь ввиду, что результат данной операции всегда округляется в сторону минус бесконечности:
Это немного сбивает с толку, но проверив результат по формуле , вы убедитесь что все верно.
IV. даже если оба числа типа int, то результат все равно будет преобразован к типу float.
V. встроенная функция пропускает числа (объекты) типа int «как есть», не выполняя над ними, абсолютно никаких действий.
VI. строго говоря эти функции не являются математическими, но они могут учавствовать в математических выражениях Python и поэтому должны обладать приоритетом.
Комплексные числа в Python (complex)
Также в Python встроены комплексные числа:
>>> >>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Числа нельзя сравнить Traceback (most recent call last): File "", line 1, in TypeError unorderable types complex() > complex() >>> print(x == y) # Однако можно проверить их на равенство False >>> abs(3 + 4j) # Модуль 5.0 >>> pow(3 + 4j, 2) # Возведение в степень, получение значения степени (-7+24j)
Кроме того, для работы с complex может применяться модуль cmath.
На этом пока что всё. Следите за новостями и не забывайте оставлять свои комментарии!
Арифметические операции
Подобно действительным числам, комплексные числа также можно складывать, вычитать, умножать и делить. Давайте посмотрим, как мы могли бы это сделать в Python.
a = 1 + 2j
b = 2 + 4j
print('Addition =', a + b)
print('Subtraction =', a - b)
print('Multiplication =', a * b)
print('Division =', a / b)
Выход:
Addition = (3+6j) Subtraction = (-1-2j) Multiplication = (-6+8j) Division = (2+0j)
ПРИМЕЧАНИЕ. В отличие от действительных чисел, мы не можем сравнивать два комплексных числа. Мы можем сравнивать только их действительную и мнимую части по отдельности, поскольку это действительные числа. Приведенный ниже фрагмент доказывает это.
>>> a (4+3j) >>> b (4+6j) >>> a < b Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: '<' not supported between instances of 'complex' and 'complex'
Комплексные числа (complex)
В Python встроены также и комплексные числа:
Также для работы с комплексными числами используется также модуль cmath.
В программировании мы всегда взаимодействуем с данными, которые не являются какой-то абстрактной субстанцией. Все данные разделяются по определенному типу. На предыдущих уроках мы узнали, про строки, списки, словари и о логическом типе данных. Сегодня, поговорим о самом базовом типе данных в Python — числах.
Почему нельзя свалить все данные в одну общую кучу и не заморачиваться с каждым типом по отдельности? Допустим, мы присвоили переменной a цифру 5: a = 5. А теперь представьте, что никакого разделения по типу данных нет. Так что находится в переменной: число или строка? Если 10 — это число, то с ним можно произвести математические действия. А если это строка, то мы имеем дело с текстом и тогда Python задействует совсем другие методы.
# объединение строк (конкатенация) d = ’10’ f = ‘негритят’ d + ‘ ‘ + f ’10 негритят’
Ключевой момент: У каждого типа данных свои методы.
Цифра 100 написанная без кавычек, относится к числовому типу данных. А цифра ‘100’ в кавычках — к строковому типу. С помощью синтаксиса, мы сообщаем Python, какой у нас тип данных. Числа в Python делятся на два вида: целое число и вещественное.
Операторы присваивания
Наиболее распространённым оператором присваивания является знак равенства (=). Он присваивает переменной слева значение справа. К примеру, в выражении v = 23 переменной v было присвоено значение 23.
В программировании часто используются составные операторы присваивания, которые выполняют операцию со значением переменной, а затем присваивают этой переменной полученное новое значение. Составные операторы объединяют арифметический оператор с оператором =. Например:
Составной оператор += выполнил сложение, а затем присвоил переменной w, значение, полученное в результате сложения.
Составные операторы часто используются в циклах.
Это позволяет автоматизировать процесс умножения чисел в заданном диапазоне.
В Python есть составные операторы присваивания для каждой математической операции:
Операторы присваивания позволяют постепенно увеличить или уменьшить значение, а также автоматизировать некоторые вычисления.
Вывод
В Python существуют два универсальных способа для извлечения корня из числа. Это возведение в необходимую степень 1/n. Кроме того, можно воспользоваться функцией из математического модуля языка, если необходимо извлечь квадратный корень числа.
Все эти методы имеют свои преимущества и недостатки. Самый наглядный это sqrt, но подходит только для квадратный корней из числа. Остальные методы не такие элегантные, но легко могут извлечь корень нужной степени из числа. Кроме того оператор ** оказался наиболее быстрым при тестировании.
Необходимо также помнить про целочисленное деление, неправильное использование которого может приводить к ошибке в вычислении.